Практическое задание к билету № 9.

Проанализируйте фрагмент конспекта урока математики с точки зрения формирования и развития ключевых компетенций в процессе изучения геометрического материала.

У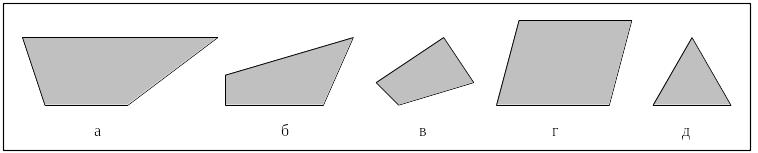 каждого ученика карточка (рис. 1).

Рис. 1

Задание 1. Стороны четырехугольника – отрезки. Измерьте их длину. Вычислите сумму длин сторон данного четырехугольника. Запишите решение.

Решение: 1 + 3 + 4 + 2 = 10 (см).

Ответ произносят: «Сумма длин сторон четырехугольника равна 10 см».

Задание 2. Измерьте длины сторон четырехугольника (рис. 1 б). Вычислите сумму длин сторон данного четырехугольника двумя способами. Запишите решение.

Решение:

I способ: 2 + 2 + 3 + 1 = 8 (см) II способ: 2 × 2 + 3 + 1 = 8 (см)

Задание 3. Измерьте стороны четырехугольника (рис. 1 в). Найдите сумму длин его сторон разными способами. Какой способ решения более рациональный?

Решение:

I способ: 2 + 2+ 2 + 4 = 10 (см) II способ: 2 × 3 + 4 = 10 (см)

Учащиеся объясняют приблизительно так. Наиболее рациональный второй способ, поскольку три стороны имеют одинаковую длину, то общую длину трех одинаковых сторон можно получить умножением длины одной стороны на 3, затеем прибавить значение длины четвертой стороны.

Учитель вводит понятие «периметр многоугольника». Объясняет: сумму длин всех сторон многоугольника называют его периметром.

– Чему равен периметр многоугольника б на рисунке 2? (– Периметр этого многоугольника равен 8 сантиметрам.)

Задание 4. Стороны четырехугольника – отрезки. Измерьте их и вычислите сумму длин сторон четырехугольника двумя способами. Запишите решение. Какой способ рациональнее?

Решение:

I способ: 2 + 2 + 2 + 2 = 8 (см) II способ: 2 × 4 = 8 (см)

Учащиеся отмечают, что способ, при котором периметр четырехугольника находят, используя прием умножения длины одной стороны на 4, то есть (2 × 4), удобнее, так как запись решения короче.

Задание 5. Измерьте длины сторон многоугольника (рис. 1 д). Вычислите его периметр рациональным способом.

Выполняя задание, учащиеся обращают внимание на равенство всех сторон треугольника д на рисунке 1 и предлагают длину одной стороны умножить на количество сторон.

Решение: 2 × 3 = 6 (см).

Для закрепления находят периметр квадрата и дают аналогичные объяснения.

Билет 9. Проанализируйте фрагмент конспекта урока математики с точки зрения формирования и развития ключевых компетенций в процессе изучения геометрического материала. (2 вариант).

Фрагмент урока по теме «Ломаная линия. Построение ломаной линии».

С лайд 1.

Задание 1. На экран телевизора или на плакате предлагаются геометрические фигуры.

Охарактеризуйте каждую фигуру? Обоснуйте свои суждения (выполняют).

Например, фигура под номером 1 – прямая линия, ее нельзя измерить, то есть длину прямой нельзя выразить числом. У нее нет начала и нет конца, она бесконечна. Через две точки можно провести только одну прямую (информацию излагают несколько учеников). Аналогично характеризуют каждую из фигур.

Учитель открывает фигуру под номером 4, предлагает рассмотреть ее.

– Кто-нибудь раньше видел изображение такой фигуры или предметов, дающих представление о такой фигуре? (– У меня дядя столяр. Я видел, как он работал с инструментом, похожим на эту фигуру. Она напоминает не до конца сложенный столярный метр.)

Учитель берет в руки столярный метр, раскрывает его («вытягивает в линию», поворачивает ребром).

– Представление о какой линии дает разложенный таким образом столярный метр? ( – О прямой линии, а, возможно, и об отрезе, если считать, что есть начало отсчета «0» и конец отсчета «100».)

– Что нужно сделать, чтобы столярный метр был похож на фигуру под номером 4? (– Нужно его «сломать».)

– Сломать? Как? Покажите. (Один ученик демонстрирует, как он «ломает» столярный метр. Затем другой, третий.)

– Вы догадались, представление о какой геометрической фигуре дает фигура под номером 4? (– Это поломанная линия. Это сломанная линия.)

– А точнее? (– Это ломанная линия.)

З адание 2. На доску проецируется слайд 2 с изображением геометрических фигур.

– Назовите ломаные линии. (– 2, 3, 4, 5.)

– Из скольких звеньев состоит ломаная линия под номером 4? Покажите ее? (– Из трех звеньев.)

– Из каких элементов состоит фигура под номером 2? Показывайте их и называйте. (– Луч, отрезок, луч.)

– Укажите ломаные линии, которые совпадают по какому-либо признаку. (– Линии под номерами 3 и 5. В них по 2 звена.)

Практическая работа. Задание 3. Начертите ломаную линию из двух звеньев. (Поставьте в тетради три точки, соедините любые две с третьей, используя линейку, обозначьте концы звеньев буквами) (рис. 1 а).

Начертите еще одну ломаную линию, состоящую из 2-х звеньев. Соедините ее концы. (Выполняют.)

– Какая фигура получилась? (– Треугольник.)

– Как, по – другому, можно назвать эту фигуру? Почему? (– Замкнутая ломаная линия. У неё звенья замкнулись.)

Закрепление. На экран проецируется слайд 3, рис. 1 в), г).

– Какая линия изображена на рис. 1 г? (– Ломаная линия.)

– Можно её назвать замкнутой линией? (– Нет, это не замкнутая ломаная линия.)

– Какая линия изображена на рис. 1 в)? Покажите ее звенья и вершины.

Учитель обобщает: «Ломаная линия – это геометрическая фигура, состоящая из точек и соединяющих их отрезков. Точки называются вершинами ломаной линии, а отрезки – звеньями. Два звена с общей вершиной называют соседними».

– Сколько звеньев у ломаной линии на рис. 1 г? Покажите ее звенья и вершины. Сколько их? Покажите соседние звенья. Отметьте красной точкой начало и конец ломаной линии. (Выполняют).

Билет 9. (анализ) 1 вариант

Проанализируйте фрагмент конспекта урока математики с точки зрения формирования и развития ключевых компетенций в процессе изучения геометрического материала.

Анализ фрагмента урока показал, что учитель реализовал цели: 1) формирование понятия «периметр многоугольника»; 2) формирование представлений о способе нахождения периметра многоугольника; 3) сформирование рациональных способов вычисления периметра многоугольника; 4) сформирование умений делать выводы и обобщения, развитие математической речи.

Выполнение задания 1 направлено на формирование практических умений, связанных с измерением длин сторон многоугольника, нахождением их суммы. Формирует компетенции: умение работать с линейкой (начало отсчета – цифра «0» должна совпадать с началом длины стороны многоугольника). Число, совпадающее с концом отрезка, выражает его длину.

Выполнение задания 2 формирует такие компетенции, как умение находить рациональный способ суммы длин сторон многоугольника (две стороны многоугольника имеют одинаковую длину, способ вычисления 2 · 2 + 3 + 1 = 8 рациональнее и др.).

Задание 3 способствует отысканию рационального способа нахождения суммы длин сторон многоугольника. (Учащиеся рассуждают: три стороны имеют одинаковую длину, то рациональным будет способ: 2 · 3 + 4 = 10.

Фрагмент урока построен так, что учащиеся постепенно приходят к рациональному способу нахождения периметра четырехугольника, осознавая: если длины сторон четырехугольника одинаковые (задание 4), то достаточно длину одной стороны умножить на количество сторон.

При выполнении задания 5 обращается внимание на равенство всех сторон. Оно способствует закреплению нахождения рационального способа периметра многоугольника.

Последовательность заданий такова, что у учащихся после выполнения двух первых заданий формируются и развиваются такие компетенции: как умение работать самостоятельно без постоянного руководства учителя; умение описывать изучаемые знания различными способами фиксации; умение осуществлять анализ геометрической фигуры, используя знания, полученные раннее; умение лаконично, четко, корректно, достоверно обосновывать свои действия; делать простейшие логические выводы; сопоставлять и обобщать полученные знания; выделять существенные признаки представленных фигур (две стороны одинаковые, три стороны одинаковые); решать практические задания по измерению длин отрезка; использовать приобретенные знания и выполнять практические действия; делать выводы и обобщения, убедительно излагать их; искать рациональные способы решения задачи.

Билет 9. (анализ) 2 вариант

Проанализируйте фрагмент конспекта урока математики с точки зрения формирования и развития ключевых компетенций в процессе изучения геометрического материала. (2 вариант).

В соответствии с уроком учитель ставит цели: 1) закрепление понятий линия, отрезок, ломаная линия, кривая линия, их свойства; 2) формирование понятий «ломаная линия, ее звенья, соседние звенья, замкнутая ломаная линия, незамкнутая ломаная линия, вершина ломаной линии»; 3) формирование совокупностей компетенций, необходимых для осознания понятия «ломаная линия»; 4) развитие творческих и познавательных способностей, речи.

Урок начат с повторения анализа свойств известных геометрических линий (отрезка, кривой, прямой). Постановка учебной задачи, связанной с формированием представлений о ломаной геометрической фигуре происходит в процессе диалога учителя и учащихся. Используя в качестве модели ломаной линии столярный метр, изображение ломаной, учитель: привлекает наблюдения учащихся из реальной жизни (я видел…, он работал с инструментом, похожим…); практическую деятельность учащихся (ученик «ломает»).

Использование вопросно-ответной формы работы в процессе выполнения задания 2, у учащихся формируется понятие «звено ломаной линии», позволяет выявить существенные признаки сходства ломаной линии (в них по два звена). Итогом фрагмента урока является практическая работа по вычерчиванию ломаной линии и формированию понятий замкнутая, незамкнутая ломаные линии.

Представленный процесс учебно-познавательной деятельности приводит к эффективному закреплению полученных знаний (слайд 3).

В процессе фрагмента урока формировались такие компетенции как: способность осознавать и рефлексировать свои действия (адекватное обоснование свойств геометрических фигур, слайд 1); умение извлекать пользу из практической деятельности самих учеников, их родителей (эта фигура напоминает не до конца сложенный столярный метр); умение на основе имеющихся знаний создавать новое и применять в своей практической деятельности (вычерчивание ломаных, определение общности и различия между замкнутой и незамкнутой ломаной линией); умение обосновывать свои действия, делать логические выводы.

Поставленные учителем цели урока достигнуты полностью.