3. 4. Методы выявления общей тенденции.

Часто в практике статистических исследований вычисление показателей динамики не дает полного представления о характере изменения уровней ряда во времени. Это связано с колеблемостью уровней во времени. Колеблемость уровней может быть вызвана действием различных факторов, которые статистика группирует (или рассматривает) в виде 4 компонентов, т.е. величина уровня ряда динамики складывается за счет действия 4 групп факторов:

– это общая или основная тенденция (образуется под воздействием общих существенных факторов);

– кратковременные, периодические (сезонные) колебания (образуются под влиянием факторов, действующих периодически в течение года);

– долговременные периодические (циклические) колебания (образуются под влиянием факторов, проявляющих себя периодически в течение длительного периода времени);

– случайные колебания, которые образуются под воздействием случайных факторов.

Общая тенденция развития явления во времени – поступательное непрерывное изменение уровней ряда динамики за длительный промежуток времени в определенном направлении.

Тренд – это некоторая аналитическая функция, при помощи которой описывают сложившуюся тенденцию ряда динамики.

Основные методы выявления общей тенденции:

1. Метод укрупнения интервалов – заключается в том, что укрупняют периоды, т.е. данные за месяцы года суммируют и получают квартальные.

2. Метод скользящей средней (механического сглаживания) – заключается в замене фактических уровней ряда динамики средними арифметическими уровнями за определенные периоды.

В основу этого метода положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.

Применение этого метода рассмотрим на данных о реализации продуктов сельскохозяйственного производства магазинами города.

Таблица 1.

Среднедневная реализация, тыс. руб.

Квартал	1-й год	2-й год	3-й год	4-й год
I II III IV	175 263 326 297	247 298 366 341	420 441 453 399	426 449 482 460

Для выявления основной тенденции развития методом скользящей средней прежде всего устанавливаются ее звенья.

Звенья скользящей средней должны составляться из числа уровней, отвечающих длительности внутригодовых циклов в изучаемом явлении. Для ряда динамики, отображающего развитие товарооборота по кварталам, скользящие средние обычно составляются из четырехчленных звеньев.

Их расчет состоит в определении средних величин из четырех уровней ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа.

; и т.д.

Таблица 2.

Год, квартал	Исходные данные,	Скользящие средние,	Сглаженные уровни с центрированием,
1	2	3	4
1-й год I кв. II кв. III кв. IV кв. 2-й год I кв. II кв. III кв. IV кв. 3-й год I кв. II кв. III кв. IV кв. 4-й год I кв. II кв. III кв. IV кв.	175 263 326 297 247 298 366 341 420 441 453 399 426 449 482 460	– 1061/4 = 265,25 1138/4 = 283,25 1168/4 = 292,00 1208/4 = 302,00 1252/4 = 313,00 1425/4 = 356,25 1568/4 = 392,00 1655/4 = 413,75 1713/4 = 428,25 1719/4 = 429,25 1727/4 = 431,75 1756/4 = 439,00 1817/4 = 454,25 –	– – 274,25 287,63 297,0 307,5 334,6 374,1 402,9 421,0 428,8 430,5 435,38 446,63 – –

Для четного числа уровней каждое значение скользящей средней приходится на промежуток между двумя смежными кварталами.

тыс. руб.

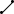
500

400

300

200

эмпирические уровни

100

сглаженные уровни

0 I II III IV I II III IV I II III IV I II III IV квартал

1-й 2-й 3-й 4-й год

Рис. 1. Реализация сельскохозяйственной продукции

по кварталам четырехлетия

3. Метод аналитического выравнивания (построение трендовой модели) – заключается в подборе математической функции, графическая линия которой будет максимально близка к графической линии изучаемого ряда динамики.

Основные правила выбора функций в зависимости от типа динамики:

1. равномерное развитие:

(уравнение прямой, парабола первого порядка)

2. равноускоренное или равнозамедленное развитие:

(парабола второго порядка)

при – ускорение

при – замедление

3. развитие с переменным ускорением (замедлением):

(парабола третьего порядка).

4. развитие по экспоненте:

(показательная функция).

5. развитие с замедлением в конце изучаемого периода:

(полулогарифмическая функция).

(уменьшается во времени)

В некоторых случаях применяются другие функции (но редко).

,… – параметры уравнения

– показатель времени

Методика построения трендовой модели:

1. фактические уровни ряда динамики переносят на график (изображаем исходный ряд динамики графически):

доверительный

интервал

Условные обозначения:

теоретические уровни

фактические уровни

уровень по прогнозу



0 2001 2002 2003 2004 2005 годы

Рис. 1 ……………

2. по характеру расположения уровней ряда на графике выбирается математическая функция: чем проще функция, тем лучше.

3. параметры уравнений и т.д. вычисляются по способу наименьших квадратов:

Формулы для расчета параметров

трендовой модели

( угла наклона)

4. промежуточные расчеты