3.3.3. Определение координат центра изгиба
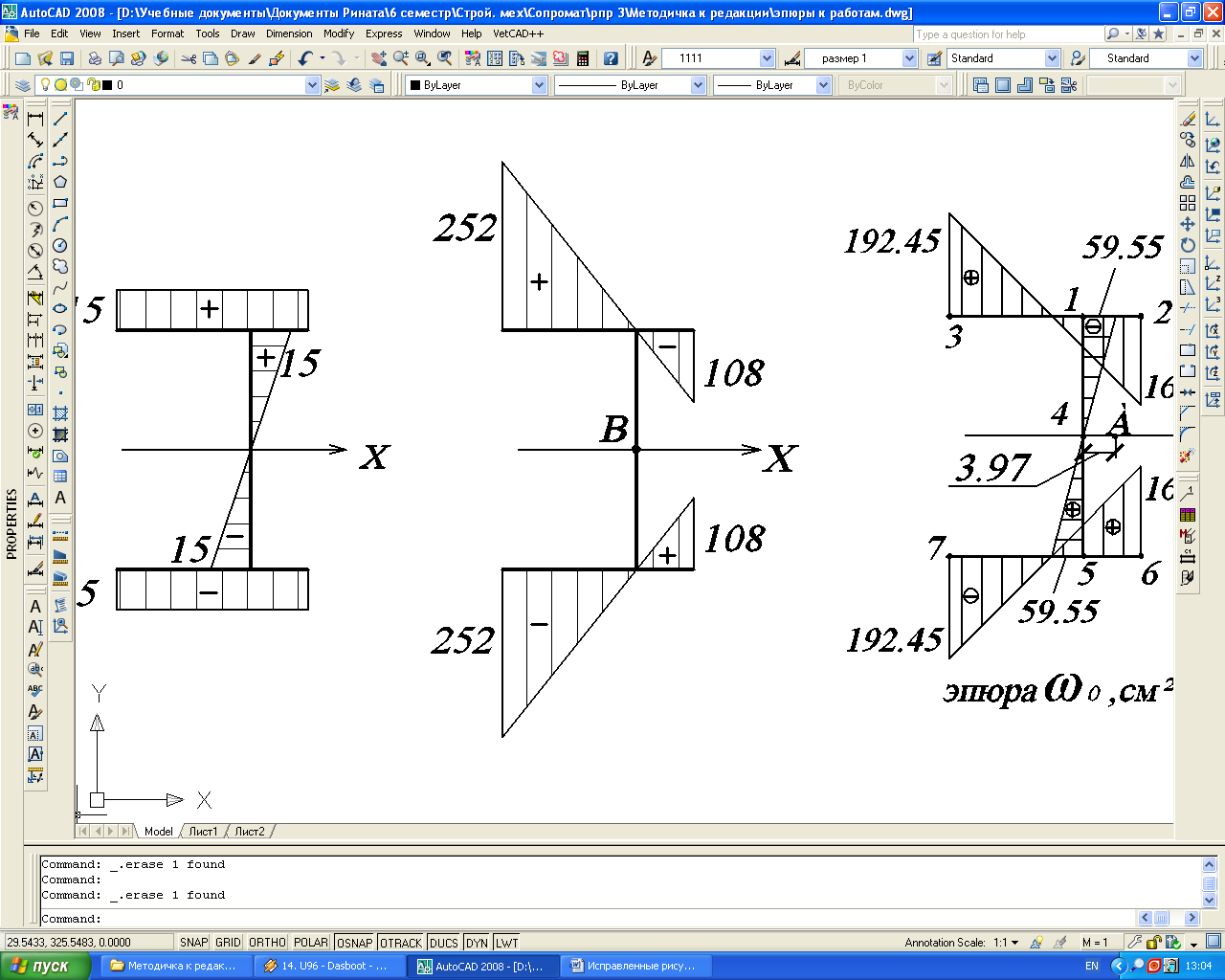
Для определения центра изгиба строим эпюру секториальных координат (рис. 43) с произвольным полюсом В и началом отсчета . B и располагаем на контуре по оси симметрии сечения.
Рис. 43.
Эпюра ωВ,
см2
;
см2;
см2;
см2;
см2;
см2.
Расположение точек взято с рис. 44.
Секториально-линейный статический момент относительно оси X вычисляем перемножением эпюр и Y по формуле
;
см5.
Определяем координаты центра изгиба
см,
откладываем от полюса B по оси Х, получаем центр изгиба А
(рис. 44).
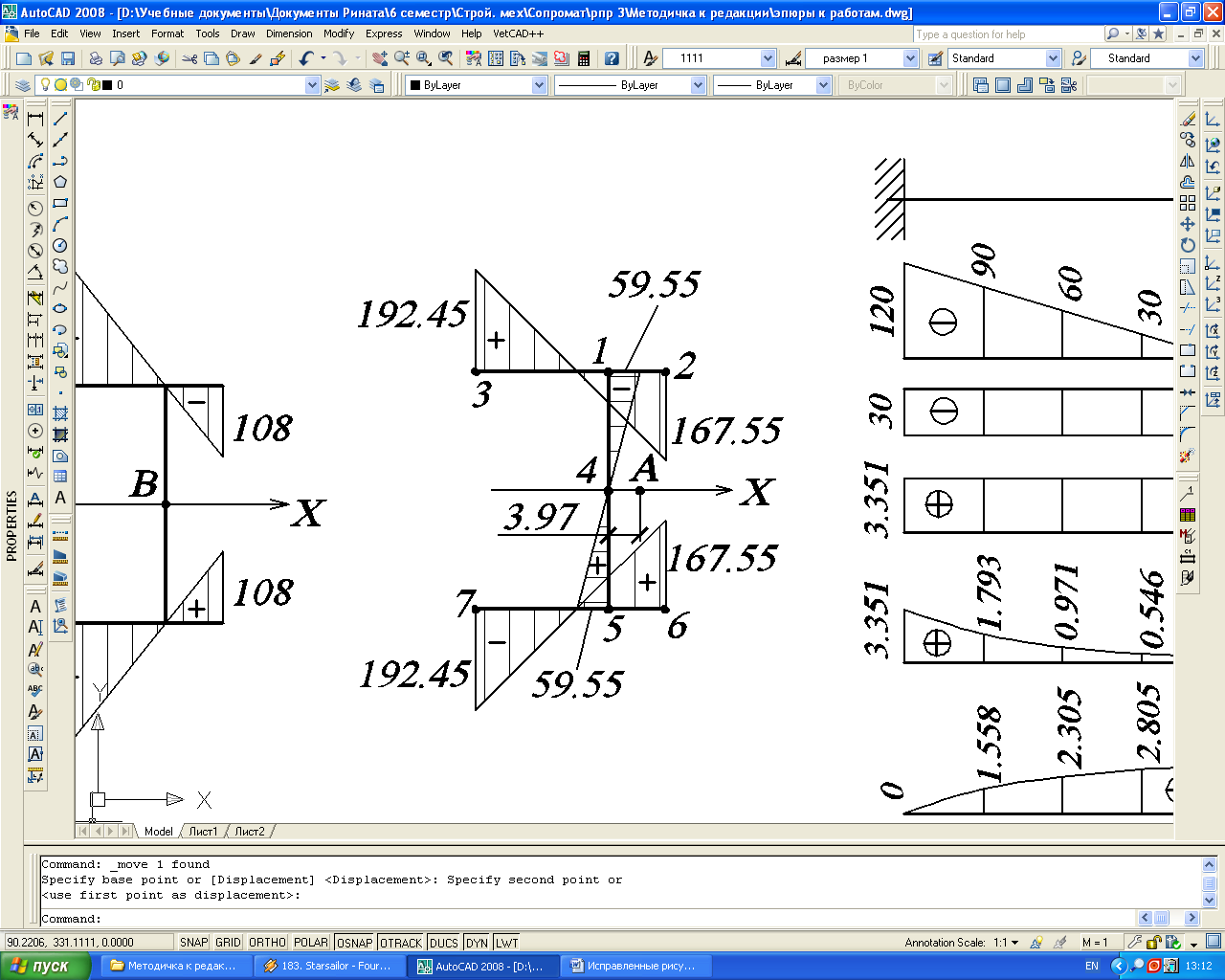
3.3.4. Построение эпюры главных секториальных координат поперечного сечения
Рис. 44.
Эпюра ω0,
см2
см2;
см2;
см2;
см2;
см2;
см2.
Проверка правильности определения положения центра изгиба:
см5.
.
Эпюра построена правильно, положение центра изгиба верное.
3.3.5. Вычисление момента инерции при чистом кручении , секториального момента инерции , изгибно-крутильной характеристики K
.
Для двутаврового сечения .
см4;
см4;
см-1
м-1.
3.3.6. Определение неизвестных начальных параметров
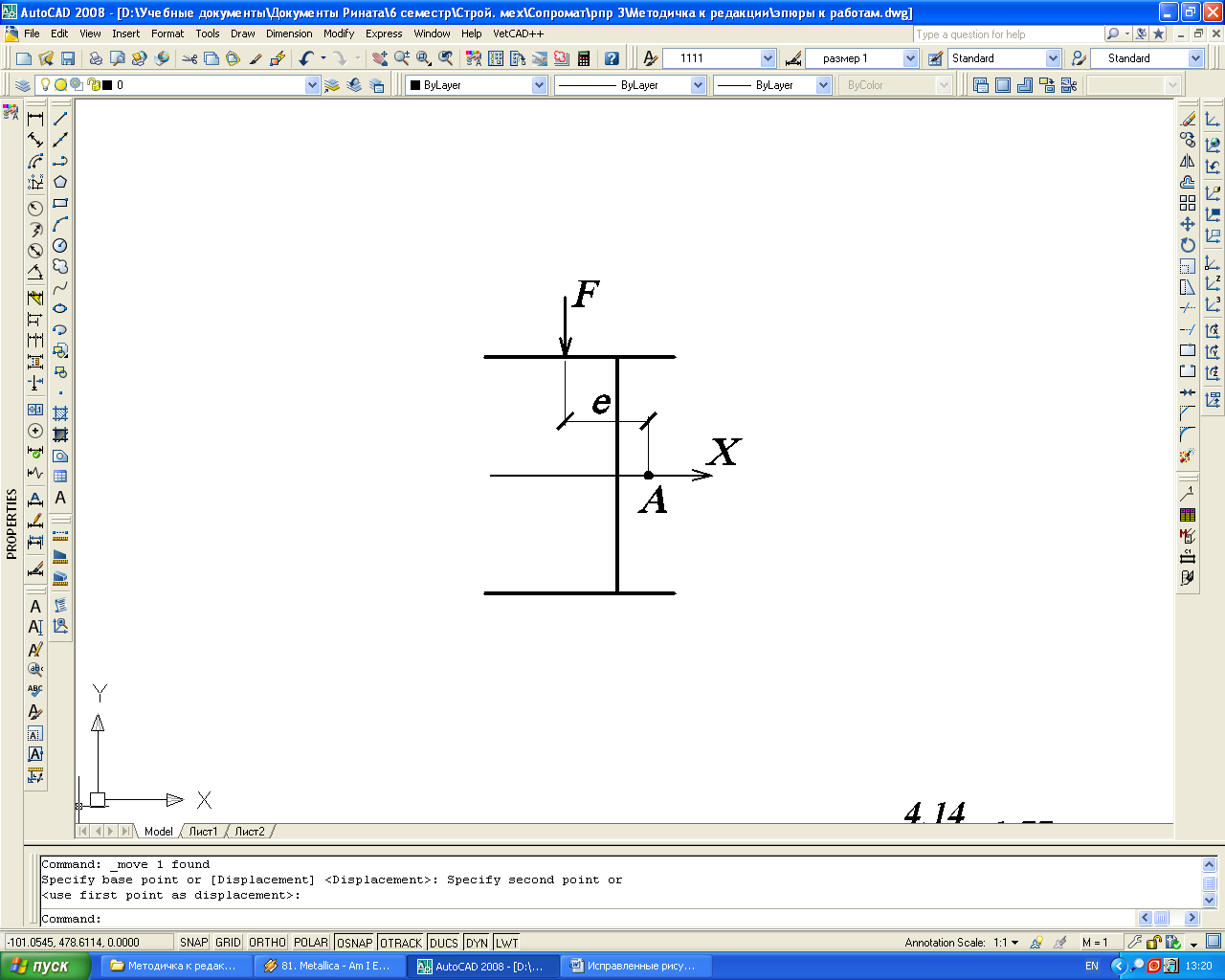
Рис. 45.
Нахождение эксцентрититета
; ; ; ; .
;
;
.
На рис. 45 показан эксцентриситет е.
см;
кН·м.
При по табл. 5
;
кН·м2.
3.3.7. Определение ординат для построения
эпюры бимоментов
По табл. 5
.
С шагом в 1 м длины балки определяем
кН·м2;
кН·м2;
кН·м2;
кН·м2;
кН·м2.
3.3.8. Определение ординат для построения эпюры
изгибно-крутящих моментов
По табл. 5
;
кН·м;
кН·м;
кН·м;
кН·м;
кН·м.
3.3.9. Определение ординат для построения эпюры
моментов чистого кручения
По табл.5
;
кН·м;
кН·м;
кН·м;
кН·м;
кН·м.
3.3.10. Определение ординат для построения эпюры
внешних крутящих моментов
кН·м;
.
Результаты вычислений внутренних усилий сводим в табл.12.
Таблица 12
Внутренние усилия
|
|
|
|
|
|
0 |
0 |
-5,2995 |
3,351 |
0 |
3,351 |
1 |
0,63 |
-2,8093 |
3,351 |
1,5580 |
1,7930 |
2 |
1,26 |
-1,4715 |
3,351 |
2,3805 |
0,9705 |
3 |
1,89 |
-0,7374 |
3,351 |
2,8050 |
0,5460 |
4 |
2,52 |
-0,3057 |
3,351 |
3,0054 |
0,3456 |
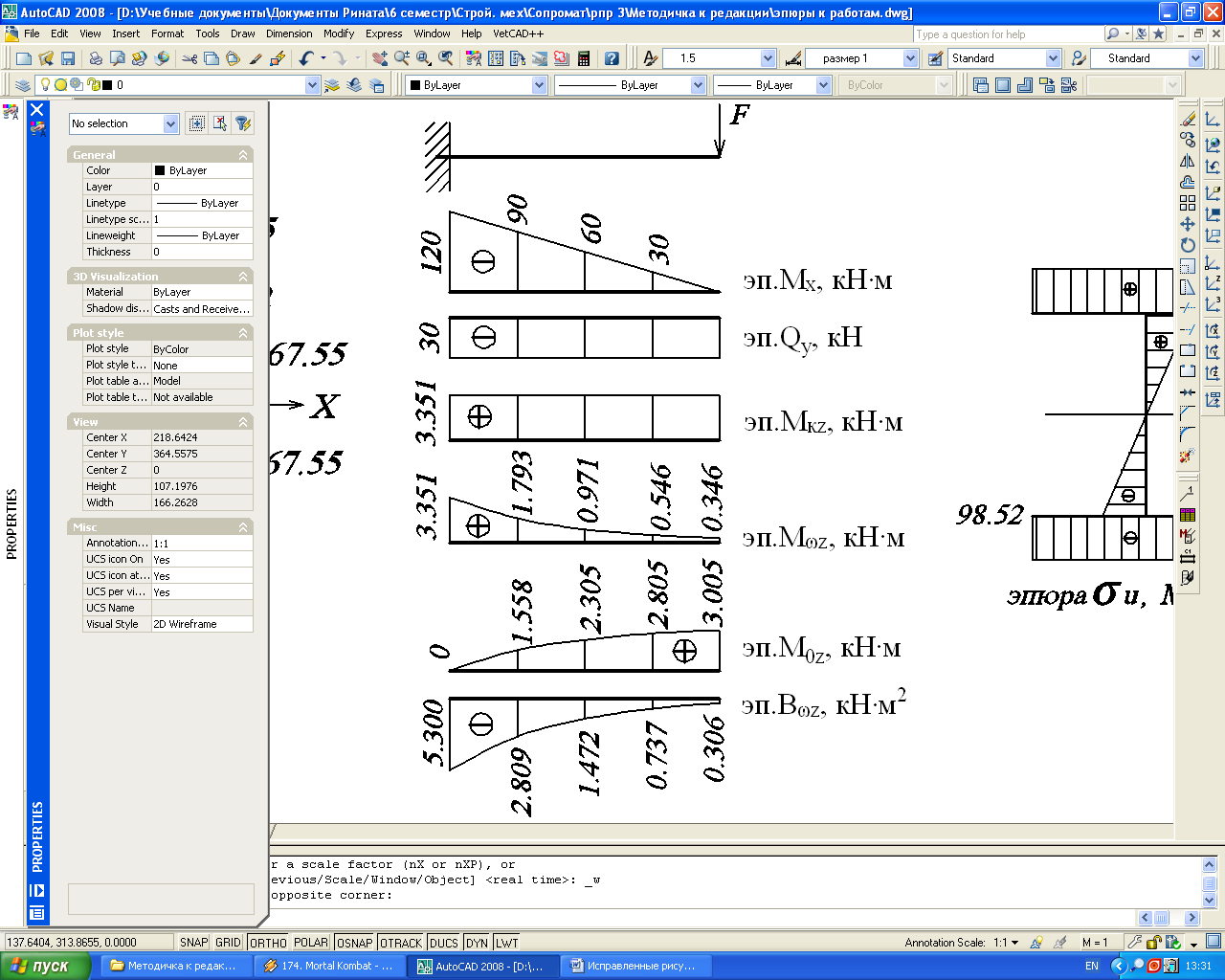
3.3.11. Построение эпюр внутренних усилий (рис.46)
Рис. 46.
Эпюры внутренних усилий