4. Линейные электрические цепи при несинусоидальных периодических токах
Периодическими несинусоидальными токами и напряжениями называются токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены несинусоидальностью источника питания или наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами.
На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что генераторы не обеспечивают идеальной синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников. В электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи.
4.1. Разложение периодических функций. Характеристики несинусоидальных величин
Из
курса математики известно, что любая
периодическая функция
,
удовлетворяющая условиям Дирихле,
может быть разложена в тригонометрический
ряд. Отметим, что функции, рассматриваемые
в электротехнике, этим условиям
удовлетворяют, в связи с чем проверку
на их выполнение условий Дирихле
проводить не нужно. При разложении в
ряд Фурье периодическая функция
представляется следующим образом:
|
(4.1) |
,
где
-
постоянная составляющая;
-
первая (основная) гармоника, изменяющаяся
с угловой частотой
,
где Т
– период несинусоидальной периодической
функции;
все
остальные члены вида
называются высшими гармониками и
отличаются друг от друга порядковым
номером k.
Высшие гармоники, для которых k
– нечетное число, называют нечетными
гармониками, для которых
k – четное число, называют четными гармониками.
В
выражении (4.1)
;
tg=
,
коэффициенты
и
определяются
по формулам:
;
. (4.2)
К
оэффициенты
ряда Фурье для стандартных функций
могут быть взяты из справочной литературы
или в общем случае рассчитаны по
приведенным выше формулам. Однако в
случае кривых, обладающих симметрией,
задача существенно упрощается, поскольку
из их разложения выпадают целые спектры
гармоник. Знание свойств таких кривых
позволяет существенно сэкономить время
и ресурсы при вычислениях.
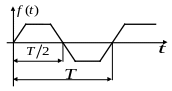
Рис. 4.1 Рис. 4.2
Рис. 4.3
Рассмотрим основные типы периодических несинусоидальных функций.
Кривые, симметричные относительно оси абсцисс. К данному типу относятся кривые, удовлетворяющие равенству
(рис.
4.1). В их разложении отсутствуют постоянная
составляющая и четные гармоники,
т.е.
,
.Кривые, симметричные относительно оси ординат. К данному типу относятся кривые, для которых выполняется равенство
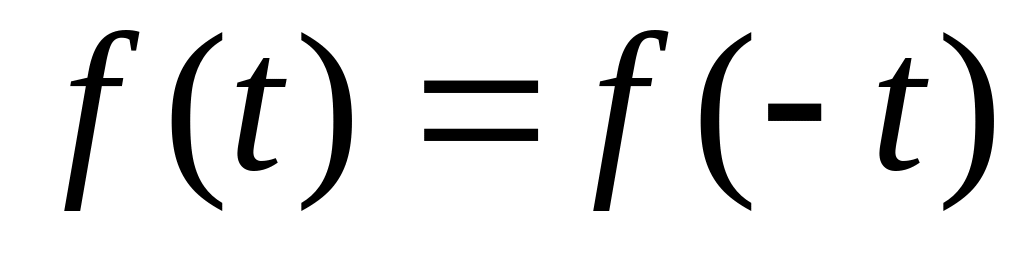(рис.4.2).
В их разложении отсутствуют синусные
составляющие, т.е.
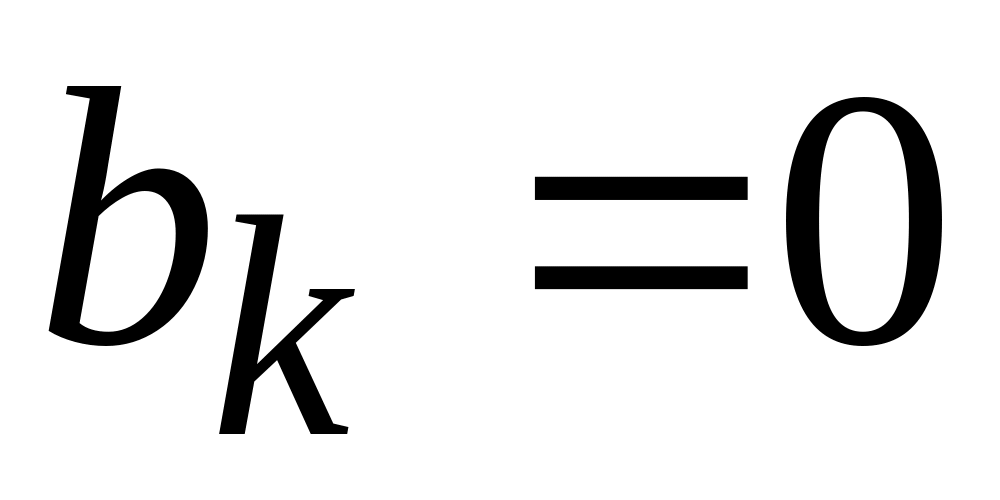.Кривые, симметричные относительно начала координат. К этому типу относятся кривые, удовлетворяющие равенству
(рис.
4.3). При разложении таких кривых
отсутствуют постоянная и косинусные
составляющие, т.е.
,
.
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
Максимальное значение -
.Действующее значение -
.
Среднее по модулю значение -
.
Среднее за период значение (постоянная составляющая) -
.
Коэффициент амплитуды (отношение максимального значения к действующему) -
.
Коэффициент формы (отношение действующего значения к среднему по модулю) -
.
Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) -
.
Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) –
.
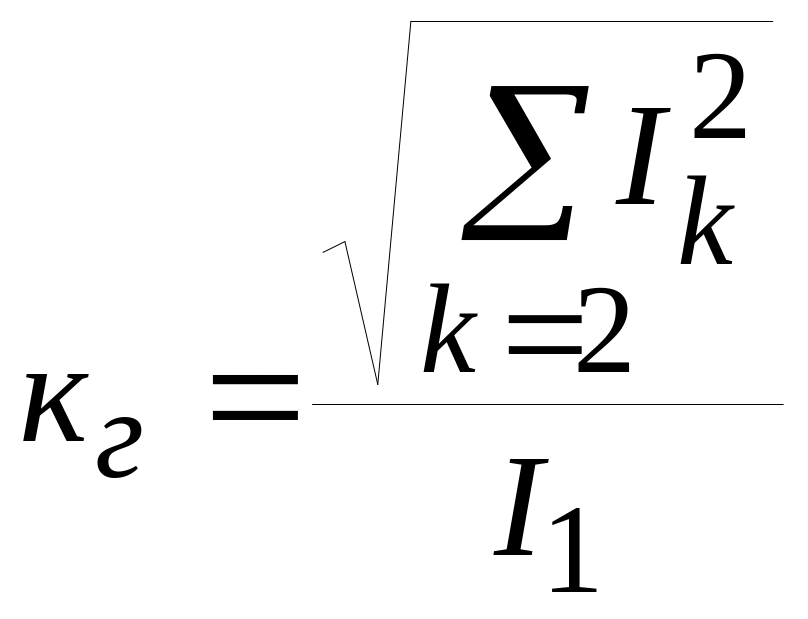Действующим значением периодической несинусоидальной переменной называется среднеквадратичное за период значение величины:
.
При наличии аналитического выражения функции i(t) и возможности взятия интеграла от ее квадрата действующее значение i(t) определяется точно. Однако в общем случае на практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.
Пусть
.
Тогда
Очевидно, что каждый из интегралов от тригонометрических функций в последнем выражении равен нулю. Таким образом,
.
или
. (4.3)
Аналогичные выражения имеют место для несинусоидальных ЭДС и напряжения.