Оцінка ефективності облігацій
Безкупонні облігації продаються за ціною нижче номіналу (з дисконтом), наприкінці терміну власник одержує платіж (шляхом погашення облігації), що дорівнює номіналу. Прикладами таких облігацій можуть служити вексель казначейства США, а на вітчизняному фінансовому ринку — державні короткострокові безкупонні облігації.
Курс або ціна на 100 одиниць номіналу розраховується як:
,
(4)
де N — номінал (у ряді закордонних джерел позначається FV - лицьова вартість); Р — ринкова ціна; К — курс (ціна в розрахунку на 100 одиниць номіналу).
Доход від придбання певної кількості безкупонних облігацій Рr (profit) буде отримано в момент їх погашення.
,
де Pr – доход від придбання безкупонної облігації; k – кількість безкупонних облігацій.
Прибутковість Y (yield) цих паперів може бути розрахована як за схемою простих відсотків (без реінвестування доходу), так і за схемою складних відсотків (у припущенні, що доход реінвестується з незмінною ефективністю). У першому випадку:
,
(5)
де YI – прибутковість без купонної облігації за схемою простих відсотків; t — кількість днів від придбання папера до його погашення.
Виразимо формулу (4) через курс:
,
звідки:
.
Прибутковість за формулою складних відсотків (Yc) може бути визначена як річна ефективна ставка:
.
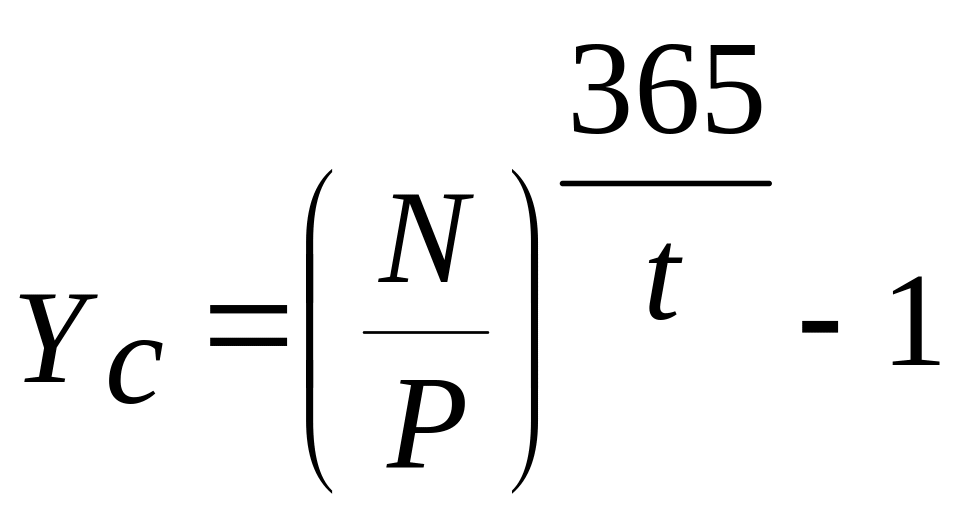(6)
Виразимо формулу (6) через курс, тобто з урахуванням формули (5) одержимо:
,
де Yc - прибутковість безкупонної облігації за схемою складних відсотків.
Завдання 3. Державні короткострокові безкупонні облігації продаються в момент випуску за певним курсом при номінальній вартості 100 грн. Розрахувати доход від придбання певної кількості паперів і доходність вкладень в них за схемою простих та складних відсотків. Дані для розрахунків знаходяться в табл. 5 (окремо для кожного варіанта).
Таблиця 5
Дані для розрахунків
Показники |
Номер варіанта |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Курс державних короткострокових безкупонних облігацій |
99 |
95 |
93 |
91 |
84 |
98 |
97 |
96 |
87 |
85 |
Кількість днів від придбання облігації до її погашення |
30 |
121 |
182 |
120 |
320 |
31 |
60 |
62 |
153 |
190 |
Необхідна кількість паперів, од. |
100 |
200 |
300 |
400 |
190 |
800 |
250 |
500 |
320 |
600 |
Оцінка ефективності акцій
Моделі оцінки вартості акцій побудовані за такими вихідними показниками: а) вид акції — привілейована чи проста; б) сума дивідендів, що передбачається до одержання в конкретному періоді; в) очікувана курсова вартість акції наприкінці періоду її реалізації (при використанні акції протягом заздалегідь визначеного періоду); г) очікувана норма валового інвестиційного прибутку (норма прибутковості) по акціях; д) кількість періодів використання акції.
Модель оцінки вартості простих акцій з постійно зростаючим рівнем дивідендів (вона відома як „Модель Гордона") має такий вигляд
,
де Pr — реальна вартість акції з постійно зростаючим (rise) рівнем дивідендів; Dl — сума останнього (last) виплаченого дивіденду; Tr – (tempo rise) темп приросту дивідендів, виражений десятковим дробом; r — очікувана норма валового інвестиційного прибутку (прибутковості) по акції, виражена десятковим дробом.
Завдання 4. Останній дивіденд, що виплачується за простою акцією складає певну суму. Акціонерне товариство постійно збільшує суму дивідендів, що виплачуються щороку, на 7 %. Знайдіть реальну ринкову вартість акції, користуючись даними табл. 6.
Таблиця 6