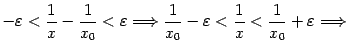Лекции (не мирэашные, но оч. похожие) + шпоры готовые к распечатке / Много всего по МАТАНУ / ОТВЕТЫ К МАТАНУ

если известно, что

и

Но это сразу следует из теоремы о пределе произведения ( теорема 2.9).

Второе утверждение означает, что

если известно, что

Это следует из того, что степенная функция непрерывна при любом , если . Как отмечалось выше, для непрерывной функции можно переставлять местами знак функции и знак предела:

В случае степенной функции , сделав замену переменного и связанную с ней замену базы, мы получим, что

Беря , получаем, что

что и требовалось доказать.     

Поскольку в этой таблице мы всегда будем рассматривать базу , для простоты записи обозначение этой базы будем пропускать и писать знак вместо .

1) . Эту формулу мы уже доказали и использовали в примерах. Эквивалентность и при означает в точности, что первый замечательный предел равен 1.

2) . Эта эквивалентность тоже была доказана выше в одном из примеров.

3) . Докажем эту эквивалентность:

4) . Докажите это в качестве упражнения, сделав замену и применив предыдущую табличную формулу.

5) . Для доказательства воспользуемся формулой . Далее, имеем:

Это означает, что доказываемая эквивалентность имеет место.

6) ( ). Для доказательства этой эквивалентности сделаем такое преобразование:

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

и мы доказали формулу 6.

В частном случае, при , получаем эквивалентность

) .

7) ( ). Для доказательства сделаем замену и выразим через : . Согласно формуле 6, при , откуда . Из непрерывности логарифма следует, что и, значит, при . В этой формуле осталось лишь сменить обозначение переменного на , чтобы получить формулу 7.

В частном случае, при , получаем эквивалентность

) .

В15.Сохранение знака непрерывной функции.Понятие равномерной непрерывности.

Напомним, что непрерывность функции в точке означает, что , то есть Тем самым непрерывность функции на интервале или отрезке означает, что При этом мы имеем право выбирать число в зависимости от и, главное, от точки .

Предположим теперь, что число можно выбрать общим для всех (но, конечно, зависящим от ). Тогда говорят, что свойство функции быть непрерывной в точке выполнено равномерно по .

Дадим теперь такое

        Определение 3.5   Пусть  -- некоторая функция и . Функция равномерно непрерывна на , если     

Приведём пример равномерно непрерывной функции.

        Пример 3.15   Рассмотрим функцию и покажем, что она равномерно непрерывна на всей числовой оси . Фиксируем число и положим . Выберем теперь любые две точки и , такие что , и покажем, что тогда . Действительно,

так как, во-первых, при всех и и, во-вторых, при всех (у нас ). Таким образом. равномерная непрерывность функции доказана.     

Лучше изучить условие равномерности по мы сможем, приведя пример, где оно нарушается.

        Пример 3.16   Пусть функция рассматривается на интервале . Если фиксирована точка , то для заданного мы можем выбрать так, что при всех таких, что ; для нахождения нужно решить неравенство относительно (напомним, что точка фиксирована):

Из чисел и выберем минимальное:

Тогда при будет . Проанализируем, однако, зависимость от : при , приближающемся к 0, значения будут убывать и стремиться к 0 (при неизменном значении ), что хорошо видно на следующем чертеже:

Рис.3.25.Изменение в зависимости от положения точки

При приближении точки к началу координат нам приходится по одному и тому же выбирать всё меньшие -окрестности точки , чтобы обеспечить выполнение неравенства . Выбрать общим для всех , очевидно, невозможно: при заданном какое бы фиксированное число ни было взято, мы можем поместить точку так близко от 0, что значения и будут отличаться друг от друга больше, чем на , хотя . Это означает, что функция не является равномерно непрерывной на интервале .     

        Теорема 3.10   Пусть и функция непрерывна на . Тогда равномерно непрерывна на .

Доказательство этой теоремы достаточно сложно и основывается на тонких свойствах системы действительных чисел, а именно, на том, что любой замкнутый отрезок является компактом⁹. Мы пропускаем здесь доказательство теоремы, отсылая за ним заинтересованного читателя к подробным курсам математического анализа, например, Никольский С.М., Курс математического анализа, т. 1. -- М.: Наука, 1991; Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления, т. 1. -- М.-Л.: ГИТТЛ, 1948 и др. годы изд.     

В качестве следствия равномерной непрерывности легко получается утверждение теоремы 3.8, а именно,

        Следствие 3.1   Любая функция , непрерывная на замкнутом отрезке , ограничена на (то есть существует такое число , что при всех ).

Приведём это доказательство (хотя теорема 3.8 была ранее доказана другим способом):

        Доказательство.     Фиксируем какое-либо число , например , и выберем такое, что при всех , для которых , будет . Разобьём на отрезки длины :

(мы положили ;¹⁰ длина последнего отрезка может оказаться меньше ). Выберем в качестве середину каждого из отрезков:

Тогда для каждого выполняется неравенство 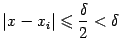и, следовательно, . Это неравенство эквивалентно такому: , или . Поскольку точек конечное число (а именно, ), то мы можем взять минимальное из чисел , , и максимальное из чисел , :

Тогда для любого верно неравенство , и осталось взять . При этом для любого будет , что означает ограниченность функции на .     

Теорема кантора Если функция непрерывна на [a,b] , то она равномерно непрерывна на [a,b] .