Силовой анализ группы Ассура (рис. 12.1, б)

Анализ начинаем с рассмотрения группы Ассура (включающей шатун 2 и коромысло 3), на которую действуют силы: веса шатуна G₂; веса коромысла G₃; силы и моменты сил инерции шатуна и коромысла, соответственно Р_и2, М_и2, и Р_и3, М_и3; реакции в шарнирах (опорах) R₀₃, R₁₂(соответственно: стойки 0 на коромысло 3; кривошипа 1 на шатун 2).

Строим в масштабе _l (м/мм) группу Ассура. В соответствующие точки прикладываем внешние силы параллельно их действию, при этом суммарное действие на звено силы и момента силы инерции заменяем одной результирующей силой инерции, создающей момент, действующий в обратном направлении угловому ускорению, и приложенной в центре качания:

• точке К для коромысла 3, лежащей на расстоянии l_О3К от оси вращения О₃

,

где l_О3S3  расстояние от оси вращения коромысла 3 до его центра тяжести, м.

• для шатуна 2, отстоящей от линии действия силы инерции Р_и2 на расстоянии

.

В шарнирах А и О₃ прикладываем реакции R₁₂ и R ₀₃, раскладывая их на нормальные и касательные составляющие. Нормальные составляющие и направляем параллельно соответственно звеньям 3 и 2, касательные и  перпендикулярно звеньям.

Рис. 12.1

Составляем уравнение моментов сил относительно точки В для второго звена (на рис. 12.1, б отмечаем плечи сил):

 М²_В(Р_i) = 0;

Полученное отрицательное значение силы говорит о том, что направление силы следует изменить на противоположное, перечеркнув крестом на схеме исходный вектор.

Значения плеч взятых с чертежа, в уравнение моментов, можно подставлять в миллиметрах, т.К. Уравнение не содержит моментов сил в чистом виде (Мi).

Составляем уравнение моментов сил относительно точки В для третьего звена

 М³_В (Р_i) = 0;

Составляем векторное уравнение сил, действующих на группу Ассура, где неизвестные записываем в конце (нормальные составляющие реакций и ):

Р_i = 0;

 .

Производим графическое сложение векторов в масштабе _Р (рис. 12.1, в). Последний вектор откладываем из полюса плана сил.

На плане получаем направления и значения сил в масштабе и . Векторно складывая касательные и нормальные составляющие, получаем абсолютные значения реакций (на рис. 12.1, в представлены пунктиром):

• соединяя точки 1 и 2 получаем  , , Н;

• соединяя точки 3 и 2 получаем  , , Н.

Для определения реакции в шарнире В следует векторно сложить все силы, действующие на звено 2 или 3, например, для звена 2

На рис. 12.1, в соединив точки 4 и 2, получаем направление действия реакции R₃₂ коромысла 3 на шатун 2.

После рассмотрения условий равновесия группы Асура переходим к определению сил, действующих на начальный механизм.

Силовой анализ начального механизма

Строим кинематическую схему начального механизма в масштабе (рис. 12.1, г), в соответствующие точки прикладываем силы: инерции кривошипа 1 Р_и1; веса кривошипа 1 G₁; реакции в шарнирах (опорах) R₂₁ - шатуна 2 на кривошип 1; R₀₁ - стойки 0 на кривошип 1; уравновешивающую силу Р_у.

Реакция шатуна 2 на коромысло 1, R₂₁ определена при рассмотрении силового анализа группы Ассура (но там определена реакция кривошипа 1 на шатун 2, поэтому при приложении её необходимо изменить направление на противоположное);

Уравновешивающая сила Р_у. (реакция двигателя на механизм), неизвестная величина, прикладывается в шарнире А перпендикулярно О₁А.

Указываем плечи действия сил относительно шарнира О₁ и составляем уравнение моментов всех сил относительно О₁:

 М_О1(Р_i)= 0;

.

Момент уравновешивающей силы (здесь r_кр – радиус кривошипа, м).

Реакцию в шарнире О₁, R₀₁, определяем из векторного уравнения равновесия всех сил, действующих на звено 1:

.

Строим план сил (рис. 12.1, д) в масштабе сил _р, Н/мм, где замыкающий вектор определяет направление и величину опорной реакции R₀₁, её значение .

Определение уравновешивающей силы методом Н.Е. Жуковского

При определении мощности двигателя и установлении его типа, расчете махового колеса, составлении характеристики регуляторов и в ряде других случаев необходимо знать только уравновешивающий момент или уравновешивающую силу, реакции в кинематических парах исследуемого механизма при этом могут остаться неизвестными. В этом случае удобнее использовать теорему Жуковского: если какой-либо механизм под действием системы сил, находится в состоянии равновесия, то повёрнутый на 90 в какую-либо сторону план скоростей, рассматриваемый как твёрдое тело, вращающееся вокруг полюса плана и нагруженное теми же силами, приложенными в соответствующие точки плана, также находится в равновесии.

Теорему Жуковского можно применить и к системе, не находящейся в равновесии. Для этого достаточно, кроме действующих сил приложить и силы инерции.

Для доказательства теоремы воспользуемся принципом возможных перемещений: если система находится в равновесии, то сумма элементарных работ на возможных перемещениях равна нулю (возможные перемещения – это перемещения допускаемые связями):

,

или разделив на dt,

,

Получаем:

,

где Р_i – задаваемые силы; _i – скорости точек приложения Р_i; _j – скорости вращения звеньев к которым приложены моменты сил М_j; N_i, N_j – мощности соответственно сил Р_i и моментов сил М_j.

Предположим, что в какой то точке звена приложена сила Р_i перенесённая параллельно самой себе в соответствующую точку повёрнутого на 90 плана скоростей. Мощность этой силы можно выразить следующим образом:

,

где h_i – перпендикуляр, опущенный из полюса плана скоростей на линию действия силы Р_i.

Так как полученное выше уравнение, определяющее величину N_i, имеет место для всех сил Р_i, действующих на другие звенья механизма, то получаем:

.

Поскольку , то:

,

что и является доказательством теоремы.

Применим метод Жуковского к нахождению приведенной, или уравновешивающей силы Р_у. Рассмотрим шарнирный четырёхзвенный механизм (рис. 12.2, а) находящийся в состоянии равновесия под действием сил: веса кривошипа 1 G₁, шатуна 2 G₂ и коромысла 3 G₃; инерции: кривошипа 1 Р_и1; шатуна 2 Р_и2, М_и2; коромысла 3 Р_и3, М_и3. Суммарное действие на звено силы и момента силы инерции заменяем одной результирующей силой инерции, создающей момент, действующий в обратном направлении угловому ускорению, и приложенной в центре качания (для шатуна 2 – K₂, коромысла 3 – K₃).

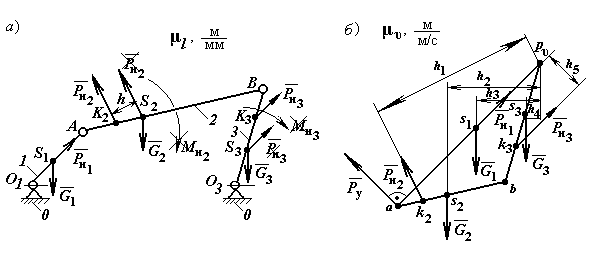
Рис. 12.2

Для приведения механизма в равновесное состояние необходимо, в какой либо точке механизма приложить уравновешивающую силу Р_у. За точку приложения уравновешивающей силы чаще всего принимают точку А начального звена, направляя её перпендикулярно к О₁А. Строим в произвольном масштабе повернутый на 90 план скоростей механизма (рис. 12.2, б) и переносим в соответствующие точки вектора внешних сил, а также уравновешивающую силу параллельно их действию. Принимая план скоростей за рычаг, нагруженный силами G₁, G₂, G₃, Р_и1, Р_и2, Р_и3 и Р_у, составляем уравнение моментов этих сил относительно полюса плана скоростей р_:

.

Из этого уравнения определяют величину уравновешивающей силы, если она получилась положительной, то направление её действия выбрано правильно. При отрицательном значении Р_у необходимо изменить её направление на противоположное.

Уравновешивающая сила является условной, и её используют лишь для вопросов, связанных с определением мощности или работы машины.