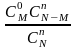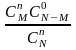Гипергеометрическое распределение

Отбор изделий для проверки, связанной, например, с их разрушением, обычно производят по схеме случайной бесповторной выборки, т.е. изделия из партии отбирают случайно, обеспечивая для каждого изделия равную с остальными возможность быть отобранным, но отобранные изделия не возвращают в партию (в генеральную совокупность).

Пусть в генеральной совокупности имеется N элементов, из них M (M<N) элементов определенного типа (отмеченных). Из этой совокупности по схеме случайной бесповторной выборки отбирают n (n<N) элементов (выборка). Обозначим через x число отмеченных элементов, попавших в выборку. Тогда x будет случайной величиной с возможными значениями 0,1,2,...,L, где L - наименьшее из чисел n и M. Число всех возможных случаев отбора n элементов из N равно , а число благоприятствующих случаев отбора m элементов из M отмеченных равно произведению 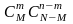. Вероятность Р(Х=m) того, что СВ Х принадлежит m, равна:

.

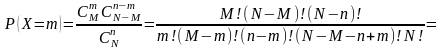
Эта формула является гипергеометрическим распределением вероятностей.

Таблица 3.4.

X	0	1	…	m	…	n
P(X=m)			…		…

Если объем выборки n очень мал по сравнению с объемом генеральной совокупности N, так что n/N<<0,1; n/M<<0,1; n/(N-M)<<0,1, то вероятности в гипергеометрическом распределении будут близки к соответствующим вероятностям в биноминальном распределении с p = M/N, т.е. расчет вероятностей для бесповторной выборки будет мало отличаться от расчета вероятностей для повторной выборки.

Математическое ожидание и дисперсия рассчитывается по формулам:

, .

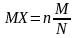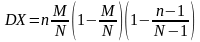Гипергеометрическое распределение используется для расчета количества испытываемых образцов в партии при разрушающих методах контроля, например, подшипников качения.

9. Показатели безотказности: вероятность безотказной работы, вероятность отказа, средняя наработка на отказ, средняя наработка до отказа, гамма–процентная наработка до отказа; остаточная наработка до отказа, интенсивность отказов, параметр потока отказов, осредненный параметр потока отказов.

Безотказность - свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки. Показатели безотказности различны для невосстанавливаемых и восстанавливаемых объектов. Основными показателями безотказности невосстанавливаемых объектов являются вероятность безотказной работы P(t), средняя наработка до отказа t_ср, интенсивность отказов λ(t) и гамма-процентная наработка до отказа t_γ.

Вероятность безотказной работы - вероятность того, что в пределах заданной наработки отказ объекта не возникнет.

Пусть t - время работы изучаемого объекта и Т - случайное время безотказной работы, т.е. время, прошедшее с начала работы до первого отказа. Тогда событие Т > t означает, что в течение времени t не произойдет ни одного отказа объекта. Для каждого значения t существует определенная вероятность того, что Т примет значение, большее t, т.е.

P(t) = P(T>t).

Функцию P(t) называют вероятностью безотказной работы. Функция P(t) является непрерывной функцией времени, обладающей следующими очевидными свойствами:

1. Р(0) = 1, т.е. в момент начала работы объекты исправны;

2. P(t) является монотонно убывающей функцией времени;

3. при t → ∞, P(t) → 0.

Вероятность отказа - вероятность того, что в заданном интервале времени или в пределах заданной наработки возникнет отказ объекта:

Из этого выражения видно, что вероятность отказа является функцией распределения случайного времени Т безотказной работы.

Вероятность безотказной работы и вероятность отказа связаны зависимостью

P(t) + Q(t) = l.

Средняя наработка до отказа - математическое ожидание наработки объекта до первого отказа

Для определения меры рассеивания наработок группы объектов до отказа необходимо применять показатель среднего квадратического отклонения наработки до отказа, статистическую оценку которого рассчитывают по формуле

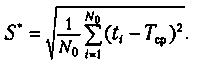(4.4)

Интенсивность отказов - условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Иными словами, интенсивность отказов - условная плотность вероятности отказа объекта для момента времени t

Гамма-процентная наработка до отказа (t_y) - наработка, в течение которой отказ объекта не возникнет с вероятностью γ, выраженной в процентах. По своему физическому смыслу гамма-процентная наработка до отказа - односторонняя нижняя доверительная граница показателя наработки, указывающая какой γ-процент объектов должен превышать установленную предельную наработку. Так, если гамма-процентная наработка до отказа 0,90, то это означает, что из большого числа объектов данной марки у 90 % отказы не возникнут в течение установленной наработки.

Гамма-процентную наработку до отказа определяют из уравнения

Р(t_y) = γ/100.

Х арактерным для эксплуатации восстанавливаемых объектов является то, что каждый из них начинает работать в некоторый момент времени, принятый за начальный, и, наработав случайную величину t₁, отказывает. После отказа объект восстанавливают, и он вновь работает до отказа, наработав случайную величину t₂ и т.д. Основные показатели безотказности восстанавливаемых объектов - параметр потока отказов ω(t) и средняя наработка на отказ t_cp.

Параметр потока отказов - отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую его наработку к значению этой наработки.