
- •Значение проблемы надёжности. Цель и задачи науки «надежность». Экономический аспект повышения надежности машин и оборудования (мо).
- •Экономический аспект надежности
- •Свойства надежности: безотказность, долговечность, ремонтопригодность, сохраняемость. Отказ и повреждение. Наработка. Критерий предельного состояния.
- •Причины и алгоритм возникновения отказов. Классификация отказов мо.
- •Классификация отказов горных машин и оборудования
- •Практическое применение дискретных распределений. Понятие потока событий (отказов). Условия простейшего (пуассоновского) потока событий: стационарность, отсутствие последействия, ординарность.
- •Биноминальное распределение (распределение Бернулли)
- •Распределение Пуассона
- •Гипергеометрическое распределение
- •Показатели долговечности: средний ресурс (срок службы), гамма–процентный ресурс (срок службы), остаточный ресурс (срок службы), назначенный ресурс (срок службы).
- •Показатели сохраняемости: вероятность сохраняемости, средний срок сохраняемости, гамма–процентный срок сохраняемости, назначенный срок хранения, остаточный срок хранения.
- •Комплексные показатели: коэффициент готовности, коэффициент неисправности, коэффициент оперативной готовности, коэффициент технического использования, коэффициент сохранения эффективности.
- •Понятие дефекта. Дефекты отливок. Дефекты обработки давлением. Дефекты сварки плавлением. Дефекты термообработки. Дефекты механической обработки. Устранимый и неустранимый дефекты.
- •Классификация процессов повреждений.
- •I. Объемные процессы повреждений
- •1. Пластическая деформация:
- •3. Изменение свойств материала:
- •II. Поверхностные процессы повреждений
- •1. Механические:
- •2. Разъедание:
- •4. Изменение свойств поверхностного слоя:
- •Параметры технического состояния объекта. Определяющие параметры технического состояния объекта. Методика прогнозирования технического состояния мо.
- •Основные мероприятия по обеспечению надежности мо при их эксплуатации. Методы снижения затрат времени на ликвидацию отказов. Определение периода замены элементов мо при параметрических отказах.
- •Определение периода замены элементов гмо при параметрических отказах
Классификация отказов горных машин и оборудования
При работе ГМО отказы возникают случайно и приводят к различным последствиям. Рассмотрим основные виды отказов элементов ГМО, которые классифицированы по ряду признаков (табл.2.1).
К опасным относят отказы, которые при возникновении, или в процессе их ликвидации, или в последующем, создают опасную для рабочих ситуацию. К ним можно отнести разрывы тяговых цепей комбайнов и стругов или нижних ветвей скребковых конвейеров, поломки перекрытий секций крепи и ряд других отказов.
Для потенциально опасных объектов кроме понятия «безопасность» важным понятием является «живучесть». Под живучестью понимают свойство объекта противостоять развитию критических отказов из–за дефектов и повреждений при установленной системе технического обслуживания и ремонта. К живучести объекта также относят его способность сохранять ограниченную работоспособность при: воздействиях, не предусмотренных условиями эксплуатации; наличии дефектов или повреждений определенного вида; отказе некоторых компонентов. Например, сохранение несущей способности элементами конструкции при возникновении в них усталостных трещин, размеры которых не превышают заданных значений.
Элемент может потерять работоспособность как в результате прекращения функционирования (разрушения элемента, заклинивания, обрыва электроцепи и т.д.) – функциональный отказ, так и вследствие выхода какого-либо параметра за пределы допускаемой величины (например, диаметральный зазор подшипника из-за износа превысил допускаемую величину) - параметрический отказ.
Внезапный – отказ, характеризующийся скачкообразным изменением значений одного или нескольких параметров объекта.
Постепенный – отказ, возникающий в результате постепенного изменения значений одного или нескольких параметров объекта.
Зависимый (независимый) – отказ, обусловленный (не обусловленный) другими отказами.
Явный – отказ, обнаруживаемый визуально или штатными методами и средствами контроля и диагностирования при подготовке объекта к применению или в процессе его применения по назначению.
Скрытый – отказ, не обнаруживаемый визуально или штатными методами диагностирования, но выявляемый при проведении технического обслуживания или специальными методами диагностики.
Сбой – самоустраняющийся отказ или однократный отказ, устраняемый незначительным вмешательством оператора.
Перемежающийся – многократно возникающий самоустраняющийся отказ одного и того же характера.
Срочный (несрочный) – отказ, устранение которого нельзя (можно) отложить до окончания рабочего цикла.
Частичный – отказ, при котором элемент еще можно использовать.
Неполомочный – отказ, не связанный с поломкой элемента (перекос секций крепи, сход комбайна с направляющих и т.д.).
Конструктивный – отказ, возникший по причине, связанной с несовершенством или нарушением установленных правил и (или) норм проектирования и конструирования.
Производственный – отказ, возникший по причине, связанной с несовершенством или нарушением установленного процесса изготовления или ремонта, выполняемого на ремонтном предприятии.
Эксплуатационный – отказ, возникший по причине, связанной с нарушением установленных правил и (или) условий эксплуатации.
Ресурсный – отказ, в результате которого объект достигает предельного состояния.
Деградационный – отказ, обусловленный естественным процессом старения, изнашивания, коррозии и усталости при соблюдении всех установленных правил и норм проектирования, изготовления и эксплуатации.
Вследствие того, что процесс возникновения отказов имеет многопричинный, случайный характер, поэтому при количественной оценке надежности ГМО используются методы теории вероятностей, теории случайных процессов и математической статистики. Прогнозирование отказов позволяет обоснованно подходить к разработке мероприятий по повышению надежности ГМО.
Понятия: событие, опыт или испытание, относительная частота, вероятность. События: достоверные, невозможные, случайные; совместные и несовместные; зависимые и независимые, противоположные. Условная вероятность события.
Понятием, наиболее употребляемым в теории вероятностей, является событие, т.е. всякий факт, который в результате опыта может произойти или не произойти. Опытом или испытанием называется физический процесс, в ходе которого осуществляются события.
Предположим, что мы проводим испытания, регистрируя каждый раз, произошло ли интересующее нас случайное событие А или нет. Относительной частотой (или просто частотой) случайного события А называется отношение числа m появления этого события к общему числу n проведенных испытаний. Относительная частота m/n обычно обладает статистической устойчивостью в том смысле, что при многократном повторении серии испытаний ее значения мало меняются, как бы группируясь относительно некоторого случайного числа. Устойчивость частоты отражает объективное свойство случайного события, заключающееся в определении степени его возможности.
Мера объективной возможности случайного события А называется его вероятностью и обозначается P(A). Именно около числа P(A) группируются относительные частоты события А. Таким образом, вероятность связана только с самим случайным событием, но относительная частота зависит ещё и от произведенных испытаний.
В классической постановке вероятность любого события А (статистическая вероятность) равна отношению числа m случаев, благоприятствующих этому событию, к общему числу n всех случаев:

Событие, которое в определенных условиях происходит обязательно, называется достоверным, не может произойти – невозможным, может произойти, но может и не произойти – случайным. Вероятность достоверного события равна единице, вероятность невозможного события равна нулю.
Если в данном опыте появление события А исключает появление события В, то такие события называются несовместными. Если в данном опыте при осуществлении события А возможно появление события В, то такие события называются совместными.
Событие
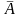 ,
состоящее в том, что событие А
в опыте не осуществляется, называются
противоположными.
Например, отказ и безотказная работа.
,
состоящее в том, что событие А
в опыте не осуществляется, называются
противоположными.
Например, отказ и безотказная работа.
Если вероятность появления события А не зависит от появления события В, то такие события называются независимыми. В противном случае события называются зависимыми.
Условной вероятностью события А, P(A/B), называется вероятность осуществления события А при условии, что произошло событие В.
Случайные события образуют полную группу, если при каждом повторении испытаний должно произойти хотя бы одно из них.
Понятие случайной или стохастической величины. Дискретные и непрерывные случайные величины. Интегральный и дифференциальный законы распределения вероятностей случайной величины. Эмпирическое распределение. Формула Стерджесса.
Важным в теории надежности является понятие случайной или стохастической величины (СВ), т.е. величины, которая в результате опыта может принять или не принять то или иное неизвестное заранее значение.
Любое правило, устанавливающее связь между возможными значениями СВ X и соответствующими ей вероятностями, называется законом распределения вероятностей СВ X.
СВ могут быть дискретными и непрерывными. Величина X называется дискретной СВ, если множество ее возможных значений представляет собой конечную или бесконечную последовательность чисел x1, x2, x3,...,xi,... и если каждое событие X=xi имеет определенную вероятность pi=Р(Х=xi).
Простой формой задания закона распределения дискретных СВ является таблица, в которой против каждого из возможных значений xi СВ Х указываются соответствующие вероятности pi.
Возможные значения Х |
x1 |
x2 |
x3 |
… |
xi |
… |
Вероятность |
p1 |
p2 |
p3 |
… |
pi |
… |
Величина Х называется непрерывной СВ, если ее возможные значения сплошь заполняют некоторый интервал. Для непрерывной СВ Х нельзя перечислить все ее возможные значения, поэтому пользуются вероятностью события р=Р(X<x).
Универсальной характеристикой дискретных и непрерывных СВ является функция распределения, называемая также интегральной функцией распределения или интегральным законом распределения.
Для дискретных СВ функция распределения имеет вид (рис.3.2):
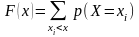 ,
,
где неравенство xi<x под знаком суммы указывает на то, что суммирование распространяется на все те значения xi, которые меньше x.
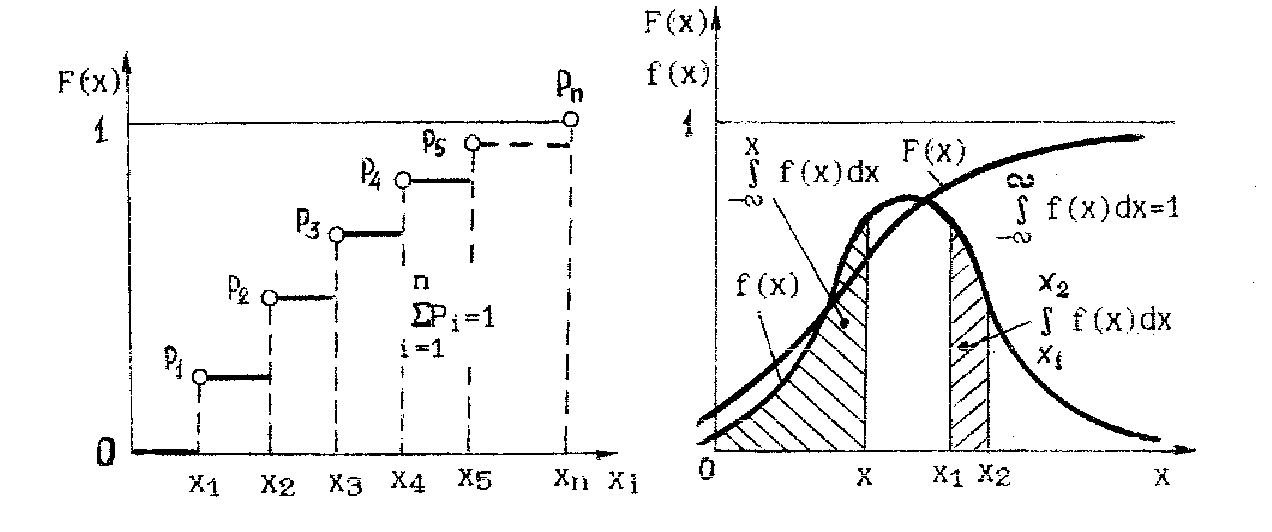
Рис.3.2. График функции распределения дискретной СВ Х
(накопленные вероятности)
Рис.3.3. Графики интегральной F(x) и дифференциальной f(x) функций распределения СВ Х
Для
непрерывной СВ функция распределения
записывается так:  .
.
Наряду с функцией распределения для вероятностного описания СВ Х используется также плотность распределения (плотность вероятности) f(x), называемая дифференциальным законом распределения СВ Х и представляющая собой производную от функции распределения f(x) = F'(x).
График плотности распределения f(x) называется кривой распределения вероятностей (рис.3.3).
Функция распределения может быть выражена через плотность распределения:
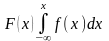 .
.
Геометрически F(x) – это площадь под кривой распределения вероятностей, лежащая левее точки х (рис.3.3). Вероятность попадания СВ Х в любой интервал (x1, x2) можно найти через плотность вероятности:
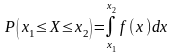
Следует подчеркнуть, что для непрерывной СВ X реальный смысл имеет только такое событие, как попадание в интервал, а не в отдельную точку.
На практике о распределении вероятностей СВ часто приходится судить только по результатам испытаний. При этом пользуются тем обстоятельством, что относительные частоты случайных событий близки к их вероятностям. Если применяется модель с непрерывной СВ X, то частоты, как и вероятности, надо относить не к отдельным значениям, а к интервалам. Это значит, что весь диапазон возможных значений СВ Х надо разбить на интервалы равной длины, примерные значения которых можно найти по формуле Стерджесса (рис. 3.4)
 (3.14)
(3.14)
где xmax и xmin - максимальное и минимальное значения СВ Х.
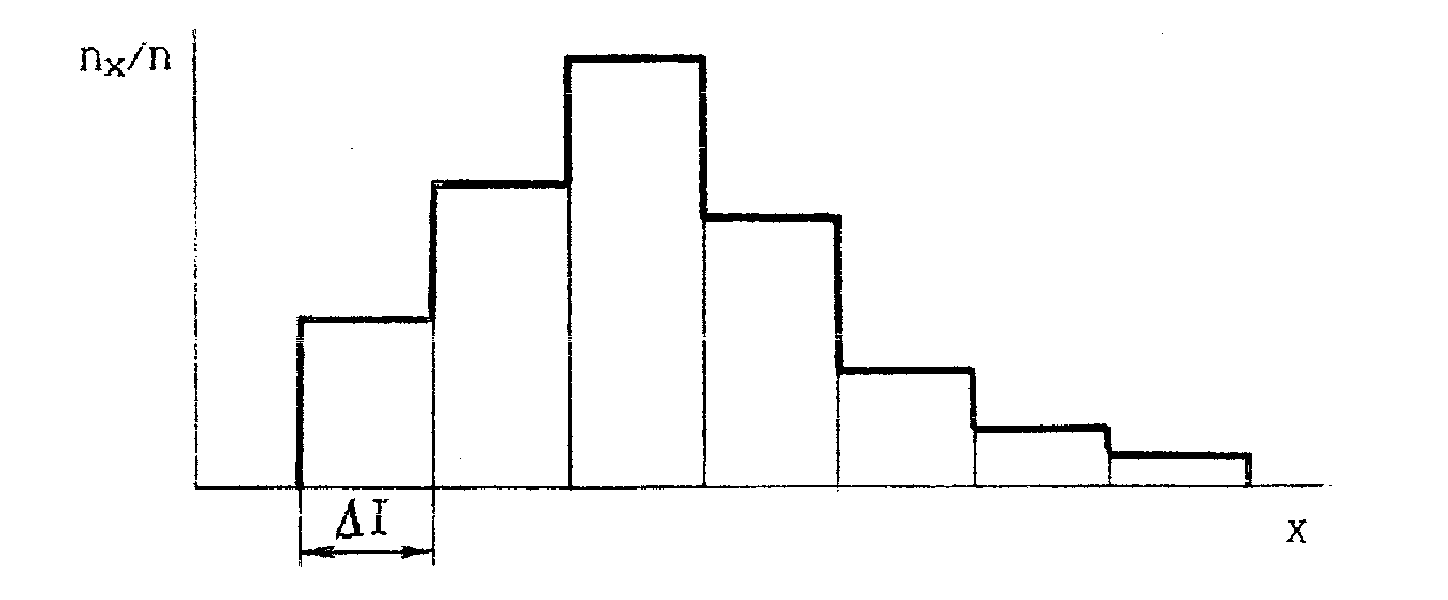
Рис. 3.4. Эмпирическое распределение, гистограмма
Произведя серию n испытаний, дающих эмпирические значения величины Х, отмечают числа nx/n попаданий результатов испытаний в каждый интервал. Затем находят отношения этих чисел к общему числу n произведенных испытаний (частоты попадания в интервалы). Зависимость частот nx/n от интервалов определяет эмпирическое распределение СВ Х.
Для удобства графической иллюстрации эмпирического распределения СВ разбивают весь диапазон ее возможных значений на интервалы равной длины и строят гистограмму (рис.3.4), откладывая по оси ординат частоты nx/n. Таким путем получают приближенное представление кривой распределения вероятностей в виде некоторой ступенчатой линии.
Основные числовые характеристики дискретных и непрерывных распределений вероятностей: математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации, мода, медиана, асимметрия, эксцесс.
Наименование |
Дискретные СВ Х |
Непрерывные СВ Х |
Математическое ожидание |
MX= |
MX= |
Дисперсия |
DX= |
DX= |
Среднее квадратическое отклонение |
X= |
|
Коэффициент вариации |
|
|
Мода М |
спектральное значение xm, при котором предшествующие и следующие за ним спектральные значения имеют вероятности меньше, чем P(xm) |
значение СВ Х, при котором плотность вероятности максимальна xM=max f(x) |
Медиана Me |
квантиль xMe уровня вероятности Р=0,5, т.е. при котором P(X<xMe)=F(xMe)=0,5. Медиана делит площадь под кривой распределения на две равные части |
|
Начальные моменты k-го порядка |
ak= |
ak= |
Центральные моменты k-го порядка |
k= |
k= |
Асимметрия (характеризует скошенность распределения) |
Sk
= если мода предшествует медиане, то Sk>0; если мода следует за медианой, то Sk<0 |
|
Эксцесс (характеризует крутость распределения) |
для плосковершинных εx <0. |
|



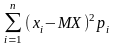

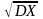 -
характеристика рассеивания СВ Х,
т.е. разброса ее значений около
математического ожидания
-
характеристика рассеивания СВ Х,
т.е. разброса ее значений около
математического ожидания -
безразмерная характеристика рассеивания
СВ Х
-
безразмерная характеристика рассеивания
СВ Х

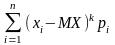

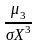 для симметричных распределений Sk=0;
для симметричных распределений Sk=0;
 ;
для островершинных кривых εx>0;
;
для островершинных кривых εx>0;