3. Геометрическое и статистическое определения вероятности

Если опыт сводится к бесконечному числу равновозможных случаев, то применяется геометрическое определение вероятности

,

где равно длине отрезка, если точки множества расположены на прямой; равно площади фигуры, если точки множества расположены на плоскости; равно объему тела, если точки множества расположены в пространстве.

ПРИМЕР 3.1. Территория нефтебазы имеет форму прямоугольника со сторонами . На территории имеется емкость диаметром 10 м. (рис. 1). Какова вероятность поражения емкости бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку равновероятное?

Р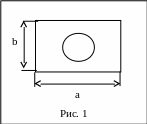 ешение: Событие А - поражение емкости бомбой, попавшей на территорию нефтебазы , где площадь заштрихованного круга; площадь прямоугольника

.

ПРИМЕР 3.2. Дети бросают мяч диаметром 0,2м в щит с круглым отверстием диаметром 1м. Какова вероятность попадания в это отверстие?

Решение: Ход решения ясен из рисунка 2, на котором “благоприятная” зона заштрихована и имеет диаметр , где R=0,5м, r=0,1м.

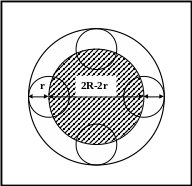
Рис.2

Тогда искомая вероятность есть .

ПРИМЕР 3.3. Внутри круга с центром в точке (0,0) и радиусом R наудачу выбирается точка N(x,y). Найти вероятность события “ ”.

Решение: В плоскости XOY построим круг и прямые , которые разделят его на четыре области. На рисунке 3 “благоприятная” область показана штриховкой.

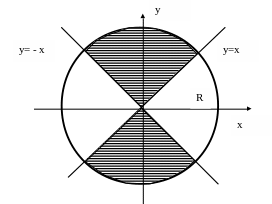
Рис.3

Непосредственно из рисунка ясно, что

.

ПРИМЕР 3.4. Внутри квадрата с вершинами (0,0),(0,1),(1,0),(1,1) наудачу выбирается точка А(x,y). Найти вероятность события “ ”.

Решение: В плоскости XOY построим заданный квадрат и прямые , которые разделят его на четыре области. На рисунке 4 “благоприятные” области показаны штриховкой.

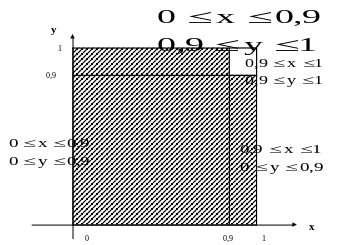
Рис.4

Непосредственно из рисунка ясно, что

.

П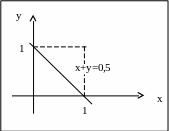 РИМЕР 3.5. Найти вероятность того, что сумма двух наудачу взятых положительных правильных дробей не больше 0,5.

Решение: Обозначим через и данные дроби. По условию задачи . Рассмотрим событие сумма дробей не больше 0,5, то есть .

Будем рассматривать как декартовы координаты точки на плоскости. Пусть площадь заштрихованного треугольника, площадь квадрата

.

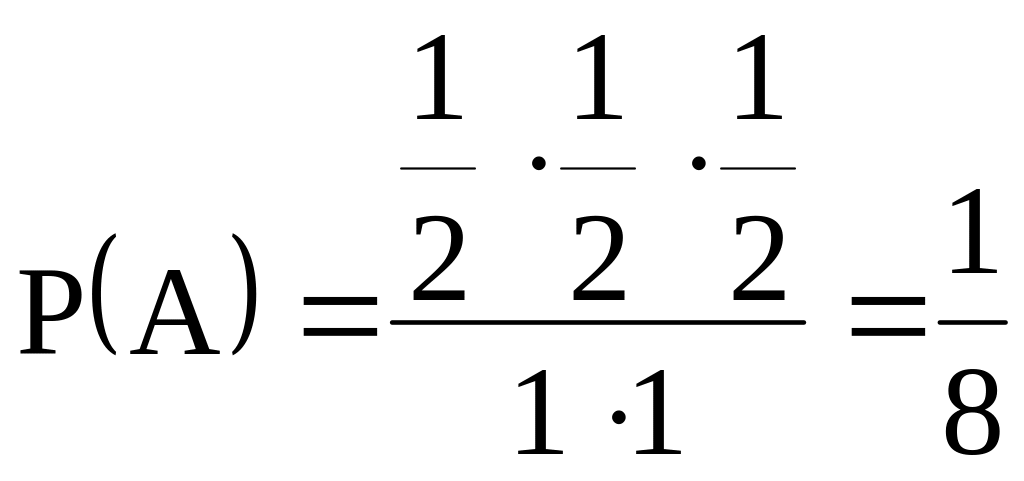П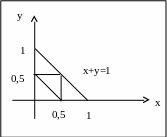 РИМЕР 3.6. Стержень единичной длины произвольным образом разламывается на три части и . Найти вероятность того, что из этих частей можно составить треугольник.

Р ешение: Элементарное событие характеризуется двумя параметрами и , ибо . На них наложены ограничения .

Пусть площадь полученного треугольника. Тогда .

Чтобы можно было составить треугольник, необходимо, чтобы сумма двух любых сторон была больше третьей ;

Этим условиям соответствует заштрихованная область

; .

Пример 3.7. Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).

Решение: Пусть и моменты прихода соответственно первого и второго студентов. Будем изображать это событие точкой с координатами на плоскости . Выберем за начало отсчета 12 часов, а за единицу измерения – 1 час. Построим на плоскости пространство элементарных событий . Это есть квадрат со стороной 1.

Р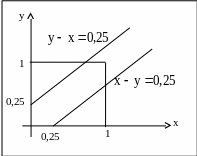 ассмотрим событие студенты встретятся. Это событие произойдет, если разность между и по абсолютной величине не превзойдет 0,25 часа (15 минут), то есть . Область, «благоприятная» этому событию, заштрихована. Ее площадь равна площади всего квадрата без суммы площадей двух угловых треугольников.

.

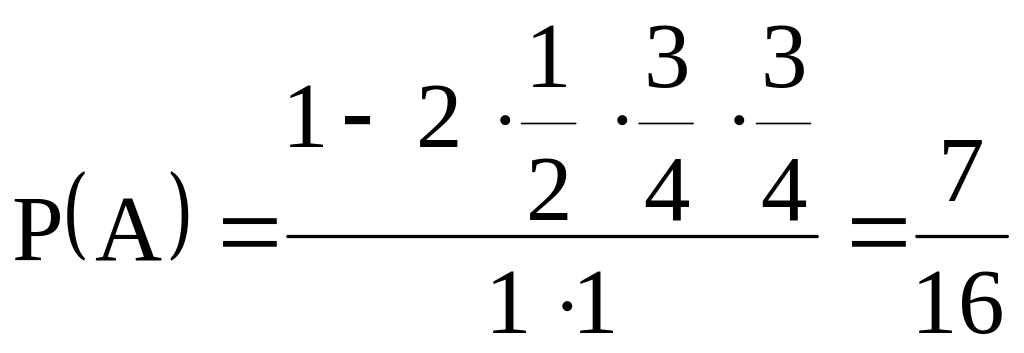Если элементарные исходы испытания неравновозможны, то нельзя применять классическое определение вероятности. Вводится статистическое определение вероятности (относительная частота события).

,

где общее число произведенных испытаний,

число испытаний, в которых событие наступило.