Задачи для самостоятельного решения

Задача 7.1. В урне 5 белых и 25 черных шаров. Вынули наугад 1 шар. Случайная величина число вынутых белых шаров. Требуется:

а) построить ряд распределения СВ ;

б) построить функцию распределения СВ ;

в) найти M(X) и D(X).

Задача 7.2. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины числа стандартных деталей среди отобранных. Найти M(X), D(X).

Задача 7.3. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: . Найти M(X), D(X) и среднее квадратическое отклонение СВ числа отказавших приборов.

Задача 7.4. Случайная величина может принимать два возможных значения: с вероятностью 0,3 и с вероятностью 0,7; причем . Найти и , зная, что и .

Задача 7.5. Дан перечень возможных значений дискретной случайной величины : , а также известно, что . Найти вероятности, соответствующие возможным значениям .

Задача 7.6. Даны независимые случайные величины и .

Х	- 1	0	1			Y	2	4
р	0,2	0,5	0,3			р	0,3	0,7

Найти математическое ожидание и дисперсию следующих случайных величин: а) ; б) ; в) .

Задача 7.7. Брошены игральных костей. Случайная величина сумма числа очков, которые выпадут на всех гранях. Найти: а) M(X); б) D(X).

Задача 7.8. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равно 0,9. Найти M(X) дискретной случайной величины числа партий, в каждой из которых окажется ровно четыре стандартных изделия, если проверке подлежит 50 партий.

Задача 7.9. Вероятность того, что в обувном магазине есть обувь, подходящей для покупателя модели, равна 0,6, а вероятность наличия обуви подходящего размера равна 0,8. Построить функцию распределения случайной величины X – числа обувных магазинов, которые посетит покупатель, если в городе три магазина.

Задача 7.10. Имеется 6 ключей, из которых только один подходит к замку. Найти закон распределения случайной величины Х - числа попыток при открывании замка, если испробованный ключ в последующих попытках не участвует. Найти M(X) и (X).

Задача 7.11. Два баскетболиста независимо друг от друга делают по одному броску в одну корзину. Вероятность попадания при одном броске равна 0,6 и 0,9 соответственно. Найти закон распределения случайной величины Х – числа попаданий в корзину. Найти M(X) и D(X).

Задача 7.12. Вероятность того, что на АЗС есть в наличии бензин марки Аи-95, необходимый автомобилисту, равна 0,9. Построить функцию распределения случайной величины X – числа АЗС, которые посетит автомобилист, если в городе пять АЗС. Найти M(X), D(X).

Задача 7.13. Случайная величина задана функцией распределения

Найти: а) параметры и D; б) плотность распределения ; в) ; г) ; д) ; е) ; ж) .

Задача 7.14. Случайная величина задана функцией распределения

Найти вероятность того, что в результате четырех независимых испытаний величина ровно три раза примет значение, принадлежащее интервалу (1/4; 3/4). Задача 7.15. Плотность распределения непрерывной случайной величины задана на всей оси функцией

.

Найти постоянный параметр .

Задача 7.16. Случайная величина задана плотностью распределения

.

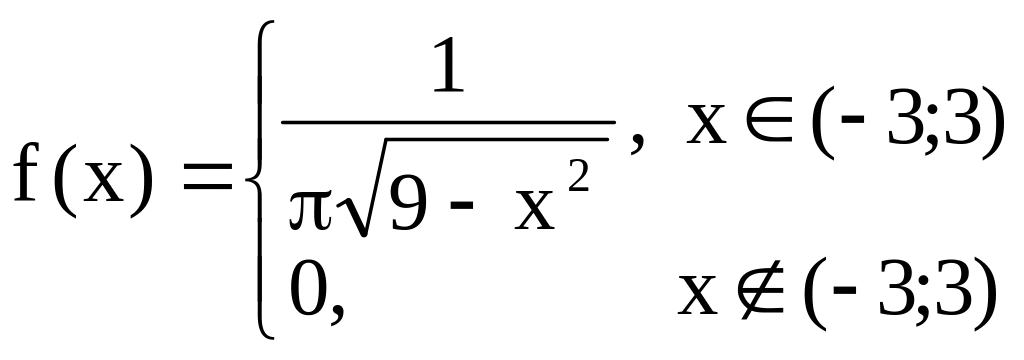Найти: а) математическое ожидание и дисперсию СВ ; б) установить, что вероятнее: в результате испытания окажется или .

Задача 7.17. Функция распределения случайной величины задана формулой . Найти: а) постоянные и ; б) плотность распределения; в) вероятность того, что СВ попадет на отрезок ; г)математическое ожидание и дисперсию СВ .

Задача 7.18. Случайная величина имеет плотность распределения

а) Построить функцию распределения .

б) Найти вероятность того, что в результате испытания .

Задача 7.19. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин.