П.1.1. Задача линейного программирования

Пример 1.

В обувном цехе для изготовления трех видов обуви используется четыре вида материалов. Исходные данные по запасам материалов, расходу их на изготовление одной пары обуви и прибыли, получаемой от реализации пары обуви, приведены в таблице 1.1. Составить математическую модель задачи.

Таблица 1.1.

Si	bi	aij
		P1	P2	P3
S1	50	0,2	0,3	0,32
S2	70	0,5	0,2	0,45
S3	80	0,4	0,1	0,21
S4	40	0,1	0,25	0,28
Cj		60	70	90

Решение. Обозначим через x₁ количество единиц продукции P₁, через x₂ – количество единиц продукции P₂, а x₃ – количество единиц продукции P₃. Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:

Конечную цель решаемой задачи – получение максимальной прибыли от реализации продукции – выразим как функцию трех переменных x₁, x₂, x₃. Реализация x₁ единиц продукции вида P₁, x₂ единиц продукции P₂, x₃ единиц продукции P₃ дает соответственно 60x₁, 70x₂, 90x₃ у.е. прибыли, суммарная прибыль:

.

Построенная линейная функция называется функцией цели и совместно с системой ограничений образует математическую модель рассматриваемой экономической задачи.

Пример 2

При откорме каждое животное ежедневно должно получать не менее 19 единиц питательного вещества S₁, не менее 18 единиц вещества S₂ и не менее 22 единиц вещества S₃. Для составления рациона используют три вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведено в таблице 1.2.

Таблица 1.2.

Питательные вещества	Количество единиц питательных веществ в 1 кг корма
	Корм I	Корм II	Корм III
S1	4	1	3
S2	2	2	6
S3	1	5	2
Стоимость 1 кг корма, руб.	16	17	24

Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.

При составлении математической модели обозначим x₁, x₂, x₃ соответственно количество кг корма I, II, III в дневном рационе.

Тогда получим систему ограничений:

Цель данной задачи – добиться минимальных затрат на дневной рацион, поэтому общая стоимость:

Пример 3

Привести к каноническому виду задачу линейного программирования.

Решение. Перейдем к задаче на отыскание максимума целевой функции. Для этого изменим знаки коэффициентов целевой функции. В целях превращения в уравнения второго и третьего неравенств системы ограничений введем неотрицательные дополнительные переменные X₄, X₅ (на математической модели эта операция отмечена буквой D). Переменная X₄ вводится в левую часть второго неравенства со знаком «+», так как неравенство имеет вид « ». Переменная X₅ вводится в левую часть третьего неравенства со знаком «-», так как неравенство имеет вид « ». В целевую функцию переменные X₄ и X₅ вводятся с коэффициентом, равным нулю. Переменную x₁, на которую не наложено условие неотрицательности, заменяем разностью Записываем задачу в каноническом виде:

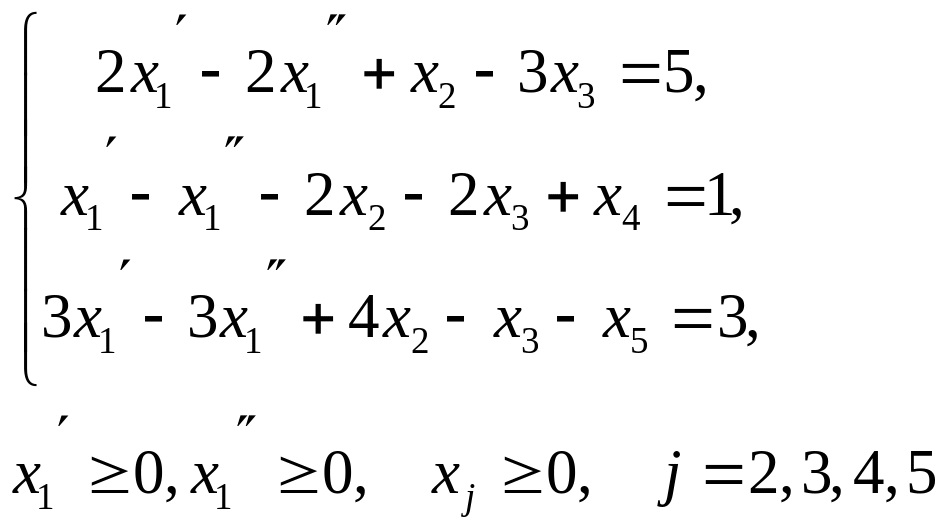
Задача 1.1.1. Малое предприятие (МП) выпускает два вида прохладительных напитков (“Радуга” и “Сияние”), предназначенных для детей и взрослых соответственно. В производстве напитков используется 4 вида сырья: газированная вода, фруктовый сироп, лед и тонизирующая добавка. Нормы расхода сырья на производство одной партии напитков и прибыль от ее реализации даны в таблице 1.1.1.

Таблица 1.1.1

Сырье	Норма расхода сырья		Суточный запас сырья
	“Радуга”	“Сияние”
Газ. вода	6 л	5 л	1200 л
Фруктовый сироп	1 л	0,5 л	150 л
Лед	0,6 кг	1,2 кг	150 кг
Тонизирующая добавка	0,1 кг	0,5 кг	30 кг
Прибыль от партии напитка	30 руб.	40 руб.

Выполните следующие задания:

1. Введите переменные.

2. Определите целевую функцию.

3. Составьте систему ограничений.

4. Определите вид математической модели задачи.

5. Преобразуйте её к другим видам задачи ЛП.

Задача 1.1.2. Автомобильный завод выпускает три вида автомобилей “Волга”: серийный вариант, повышенной комфортности и представительского класса. Время сборки на конвейере одного автомобиля составляет для этих типов автомобилей 1 мин., 2 мин. и 3 мин., а расход бензина на 100 км равен 10 л, 12 л и 15 л соответственно. Экологическое законодательство требует, чтобы средний расход бензина не превышал 13 л. Прибыль от реализации одного автомобиля составляет 6, 10 и 25 тысяч рублей соответственно.

Выполните следующие задания:

1. Введите переменные.

2. Определите целевую функцию.

3. Составьте систему ограничений.

4. Определите вид математической модели задачи.

5. Преобразуйте её к другим видам задачи ЛП.

Задача 1.1.3. Диетолог разрабатывает новую диету, состоящую из сливочного масла, натуральных бифштексов (мяса), хлеба и яблочного сока. Содержание калорий, белков, жиров, углеводов и холестерина (в 100 г продукта), а также максимальные и минимальные нормы их потребления (в день) приведены в таблице 1.1.3. Здесь же указана цена в рублях 100 г соответствующего продукта.

Таблица 1.1.3

Элемент питания	Содержание в 100 г продукта				Норма потребления
	масло	мясо	хлеб	сок	мin	мах
Калории	800	280	245	80	2400	2800
Белок	0,6 г	15 г	8 г	0 г	60 г	60 г
Жир	20 г	5 г	0 г	0 г	0 г	30 г
Углеводы	0 г	0 г	5 г	10 г	10 г	40 г
Холестерин	0,15 г	0,08г	0 г	0 г	0 г	0,5 г
Цена	3	4	0,5	1

Выполните следующие задания:

1. Введите переменные.

2. Определите целевую функцию.

3. Составьте систему ограничений.

4. Определите вид математической модели задачи.

5. Преобразуйте её к другим видам задачи ЛП.

Задача 1.1.4. Из двух видов сырья завод получает сплав меди, олова и цинка. Процентное содержание компонентов в сырье обоих видов дано в таблице 1.1.4.

Таблица 1.1.4

Компонен-ты	Содержание компонент в сырье
	сырье №1	сырье №2
Медь	10%	25%
Олово	30%	20%
Цинк	15%	10%

Цена 1 т сырья составляет 2000 руб. и 3000 руб., а имеющиеся запасы не превышают 5 и 12 т для 1-го и 2-го видов сырья соответственно. Полученный сплав должен содержать не более 1 т цинка, не менее 2 т олова, а содержание в нем меди должно составлять не менее 15%.

Выполните следующие задания:

1. Введите переменные.

2. Определите целевую функцию.

3. Составьте систему ограничений.

4. Определите вид математической модели задачи.

5. Преобразуйте её к другим видам задачи ЛП.

Задача 1.1.5. Сельскохозяйственное предприятие обязалось поставить в два магазина 25 и 35 т картофеля соответственно. Предприятие располагает тремя складами с запасами картофеля 15, 20 и 30 т соответственно. Расходы на поставку 1 т картофеля с каждого из складов в оба магазина даны в таблице 1.1.5.

Т аблица 1.1.5

Магазины Склады	№1	№2
№1	20 руб.	45 руб.
№2	30 руб.	20 руб.
№3	40 руб.	35 руб.

Выполните следующие задания:

1. Введите переменные.

2. Определите целевую функцию.

3. Составьте систему ограничений.

4. Определите вид математической модели задачи.

5. Преобразуйте её к другим видам задачи ЛП.

Задача 1.1.6. Предприниматель-заготовитель, располагающий суммой 10000 рублей и фургоном грузоподъемностью 5 тонн, решил закупить у фермера лук и картофель. Закупочная цена лука - 1,5 руб/кг, картофеля - 1 руб/кг, в то время как цена реализации предполагается 2,5 руб/кг и 1,5 руб/кг соответственно. Запасы картофеля у фермера составляют 4 тонны, а лука - 3 тонны.

Выполните следующие задания:

1. Введите переменные.

2. Определите целевую функцию.

3. Составьте систему ограничений.

4. Определите вид математической модели задачи.

5. Преобразуйте её к другим видам задачи ЛП.