Доказательство.

По индукции легко показать, что

Следовательно,

Отсюда

В силу лемм 1 и 2 имеем

Кроме того, из (5) и (6) следует, что

Применим правило останова (4). Тогда и из (11) и (15) получим . (17)

Для , поэтому . Итак, для

Из (13) и (18) получаем при или

(т.к. из (13) ). Если при этом при , то используя (10), получим так как из (12) Если же для некоторых последовательность окажется ограниченной, то и в этом случае

Действительно, из (17) имеем Следовательно, и по Лемме 3 получаем, что Отсюда ч.т.д.

Имеет место Теорема 2. Пусть выполнены условия теоремы 1 и пусть тогда справедливы оценки

Доказательство. Имеем Воспользовавшись (18), получим , откуда . При помощи неравенства моментов оценим

(см. (17)). Тогда, поскольку соотношение (5) справедливо для любых n, то ч.т.д.

Замечание 1. Порядок оценки (19) есть и он оптимален в классе задач с истокопредставимыми ре­шениями

Замечание 2. Хотя формулировка теоремы 2 даётся с указаниями степени представимости s и истокопредставимого элемента z, на практике их значение не потребуется, так как они не содержатся в правиле останова (4). И тем не менее в теореме 2 утверждается, что будет автоматически выбрано количество итераций т, обеспе­чивающее оптимальный порядок погрешности. Но даже если истокопредставимость точного решения отсутствует, останов по невязке (4), как показывает теорема 1, обеспечивает сходимость метода, т.е. его регуляризующие свойства.

56. Понятие корректно поставленной и некорректно поставленной задачи. Пример. Неявный метод простой итерации решения некорректных задач с априорным выбором числа итераций.

Пусть в гильбертовом пространстве Н требуется решить , где А – ограниченный, положительный и самосопряжённый оператор. Нуль не является собственным значением оператора, поэтому уравнение (1) имеет единственное решение. Предполагаем, что , поэтому задача (1) неустойчива и зн. некорректна.

Опр. Задача определения решения из пространства Х по известной правой части наз. устойчивой на пространствах Х и У, если Опр. Следуя Ж.Адамару, задачу отыскания из ур-я (1) наз. корректной (корректно поставленной), если при любой фиксированной правой части из У её решение: 1) существует в пространстве Х; 2) единственно в Х; 3) устойчиво в Х. Если хотя бы одно условие не выполняется, то задачу наз. некорректной (некорректно поставленной).

Пример некорректной задачи: Х=У=L₂(0,1). Интегральное уравнение Фредгольма 1-ого рода .

Опр. назовём задачу (1) корректной по Тихонову на множестве , а само множество М - её множеством корректности, если: 1) точное решение задачи существует в классе М; 2) принадлежащее множеству М решение задачи единственно для любой правой части у из множества ; 3) принадлежащее множеству М решение задачи устойчиво относительно любой правой части у из N. В случае нарушения любого из этих условий задачу (1) наз. некорректной.

Будем решать ур-е (1) с помощью неявного итерационного метода:

(2)

Предполагая существование единственного точного решения x уравнения (1) при точной правой части у, ищем его приближение при приближённой правой части , . В этом случае метод примет вид

(3)

Под сходимостью метода (3) понимается утверждение о том, что приближение подходит к точному решению х ур-я (1) при подходящем выборе n и достаточно малых , т.е. .

Справедлива

Теорема 1. Итерационный процесс (2) при условии (4) сходится в исходной норме гильбертова пространства .

Док-во:

По индукции нетрудно показать, что . Используя интегральное представление самосопряжённого оператора спектральная ф-я, . Так как уравнение (1) имеет по предположению единственное точное решение, то и, следовательно,

.

Разобьём полученный интеграл на 2 интеграла

При условии (4) величина , тогда

.

Следовательно, , т.е. итеративный процесс (2) сходится, ч.т.д.

Покажем, что при тех же условиях процесс (3) можно сделать сходящимся, если нужным образом выбрать число итераций n в зависимости от уровня погрешности . Имеет место

Теорема 2. При условии итерационный процесс (3) можно сделать сходящимся, если нужным образом выбрать число итераций n так, чтобы .

Доказательство:

Будем считать и рассмотрим разность . Как показано ранее, . Воспользовавшись интегральным представлением самосопряженного оператора , получим

По индукции нетрудно показать, что .

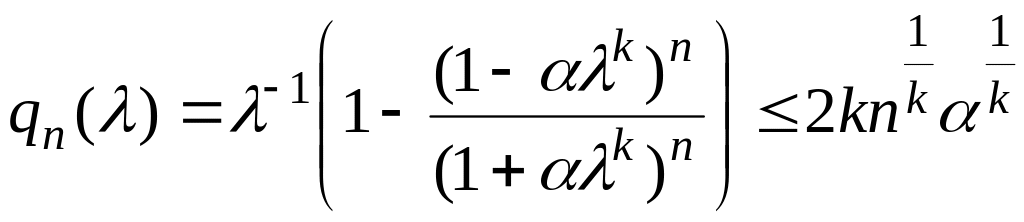Тогда . Поскольку и, как показано ранее, , то для сходимости метода (3) достаточно, чтобы , ч.т.д.

Теорема 3. Если точное решение ур-я (1) истокопредставимо, т.е. , то при условии оценка погрешности для метода (3) . .

58.Метод обобщенного суммирования рядов для решения некорректных задач.

При приближенном решении математических задач сущ. является вопрос корректно поставленной задачи.

Задача наз. устойчивой - если бесконечно-малой вариации правой части уравнения, соответствует бесконечно-малые вариации левой части.

Задача наз. корректной по Адамару, если при любой фиксированной правой части правой части y=y₀, точное решение: существует в x, единственно, устойчиво.

Задача наз. корректной по Тихонову на мн-ве X, если: точное реш. сущ в M, ед при любом у из N, устойчиво.

Метод обобщенного суммирования рядов предназначен для решения некорректных задач. Рассмотрим его на примере уравнения: в пр-ве L₂(0,1) c полным симметр. квадратично суммируемым ядром A(t,s). λ=0-принадлеж S(p), но не явл. его собственным значением. λi – собств. значения ядра, располож. в порядке убывания.

zi(t) – соотв. полная, ортонормированная система собственных функций уравнения: где, . В этом случае решение запишется:

Возьмем вместо точного y(t) – приближенное y_δ(t) такое, что , или, что то же самое, вместо точных коэф. Фурье – приближенные , . Требуется по этим точным приближениям коэф. Фурье построить аппроксимацию для точного решения. В этом случае решение запишется: - т.к. задача не корректна, то этим рядом пользоваться нельзя. Не будем доводить суммирование этого ряда до конца, а воспользуемся некоторым конечным отрезком: . Покажем, что это действительно можно сделать.

Рассмотрим: . Первый член справа , . Следов.: если n выбрать так, чтобы , то , при n=n(δ) →∞, для δ →0.

Оценить невозможно без дополнит. предположения, т.к. неизв., и может быть сколь угодно малой скорость убывания нормы. Потребуем чтобы x было истокопредставимо: . Из этого предположения следует, что сходится ряд x(t)=Az отсюда и что . Оценим , получим .

Найдем, при каком n эта оценка – оптимальна (принимает мин. значение).

, отсюда , з.н. t*- min.

Получим оптимальную оценку: при .

Если имеет место s-кратная истокопредставимость, то