5.1.4. Примеры расчета и конструирования элементов стропильной фермы

Для примера на рис. 5.1 представлена геометрическая схема фермы с шарнирным примыканием к колонне сбоку, приведены расчетные усилия в элементах фермы. При жестком сопряжении стропильной фермы с колонной учитываются усилия, вызванные опорными моментами.

Материал конструкций – сталь класса С245; R_y = 24 кН/см².

При расчете фермы принят коэффициент надежности по ответственности _n = 1.

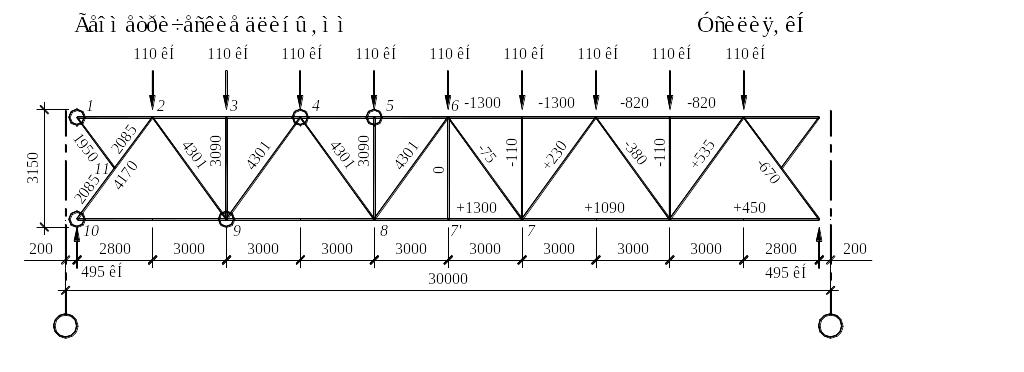
Рис. 5.1. Расчетная и геометрическая схема фермы

Пример 5.1. Подобрать сечение верхнего сжатого пояса фермы из двух уголков по расчетному усилию N = –1300 кН. Расчетные длины стержня: в плоскости фермы l_x = 300 см, из плоскости l_y = 300 см (при шаге прогонов кровли d = 3 м).

Толщина узловых фасонок назначается в зависимости от максимального усилия, действующего в стержнях решетки (как правило, в опорном раскосе). Принимаем толщину фасонки t_ф = 14 мм согласно табл. 5.5 при максимальном усилии в опорном раскосе N_p,max = –670 кН (рис. 5.1).

Поскольку l_y = l_x, принимаем сечение сжатого пояса из двух равнополочных уголков (рис. 5.2).

Таблица 5.5

Рекомендуемые толщины фасонок

Максимальное усилие в стержнях решетки, кН	До 150	160–250	260–400	410–600	610–1000	1010–1400	1410–1800	Более 1800
Толщина фасонки, мм	6	8	10	12	14	16	18	20

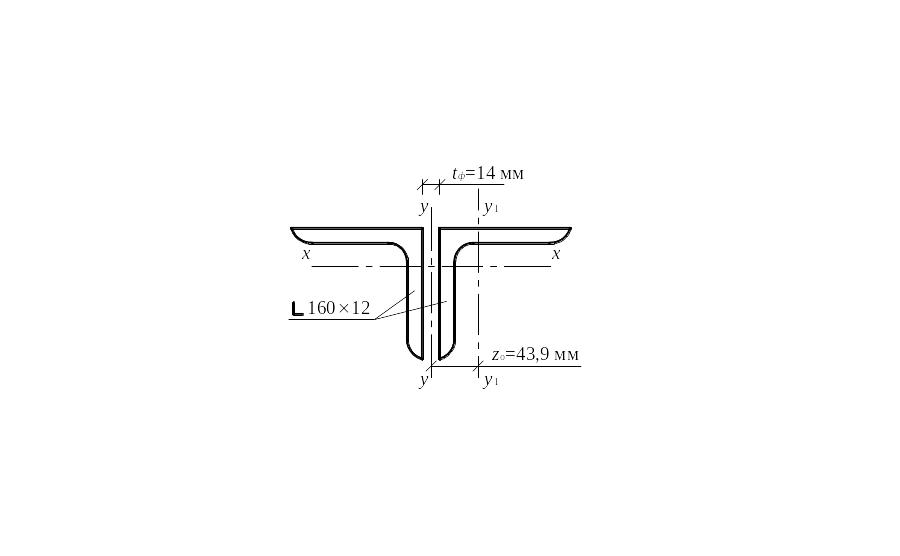
Рис. 5.2. Сечение пояса (к примеру 5.1)

При подборе сечений поясов стропильных ферм гибкость предварительно принимается λ = 60–90 (бóльшие значения гибкости – при меньших усилиях в элементе), но не более λ_и = 120 при полном использовании несущей способности колонны (см. табл. 5.1).

Задаемся λ = 70.

Условная гибкость

Рассматриваемому тавровому сечению соответствует тип кривой устойчивости «с» (см. табл. 4.5). При условной гибкости = 2,39 коэффициент устойчивости при центральном сжатии  = 0,674 (см. табл. 4.6).

Из условия устойчивости сжатого стержня определяем требуемую площадь сечения пояса:

А_тр = N_n/(φR_yγ_с) = 1300 ∙ 1 / (0,674 24 ∙ 1) = 80,36 см².

Требуемый радиус инерции

i_тр = l_x/λ = 300 / 70 = 4,29 см.

По требуемым значениям площади и радиуса инерции из сортамента (см. приложение В, табл. В.4) принимаем сечение из двух равнополочных уголков ∟160×12/ГОСТ 8509-93. Площадь сечения А = 37,39 ∙ 2 = 74,78 см²; радиус инерции сечения уголка i_х = i_y1 = 4,94 см; расстояние от центра тяжести уголка до наружной грани полки z_о = 4,39 см.

Определяем радиус инерции составного сечения из двух уголков при зазоре между уголками а = t_ф = 14 мм:

см.

Подсчитываем гибкости в главных плоскостях:

λ_х = l_x/i_х = 300 / 4,94 = 60,7;

λ_у = l_у/i_у = 300 / 7,1 = 42,25.

Наибольшая условная гибкость

По наибольшей гибкости согласно табл. 4.6 находим минимальный коэффициент устойчивости при центральном сжатии φ_min = 0,732.

Производим проверку устойчивости верхнего пояса:

Резерв несущей способности

В процессе монтажа (раскрепляющие верхний сжатый пояс прогоны или плиты покрытия отсутствуют) необходимо закрепление верхнего сжатого пояса фермы в его узлах инвентарными съемными связями располагаемыми на расстоянии

l_у ≤ i_уλ_и = 7,1 ∙220 = 1562 см ≈ 15 м.

Пример 5.2. Подобрать сечение верхнего сжато-изгибаемого пояса фермы при действии на него осевого усилия N = –1300 кН и внеузловой нагрузки F = 55 кН, приложенной в середине панели d. Расчетные длины пояса l_х = l_у = d = 300 см.

Для сжатых поясов ферм, воспринимающих поперечную внеузловую нагрузку, значение изгибающего момента M принимается равным наибольшему моменту в пределах средней трети длины панели пояса, определяемому из расчета пояса как упругой неразрезной балки (рис. 5.3).

Определяем изгибающий момент в середине панели пояса:

M = 0,9Fd/4 = 0,9 ∙ 55 ∙ 300 / 4 = 3712, 5 кН∙см.

Эксцентриситет приложения силы

е = M/N = 3712,15 / 1300 = 2,86 см.

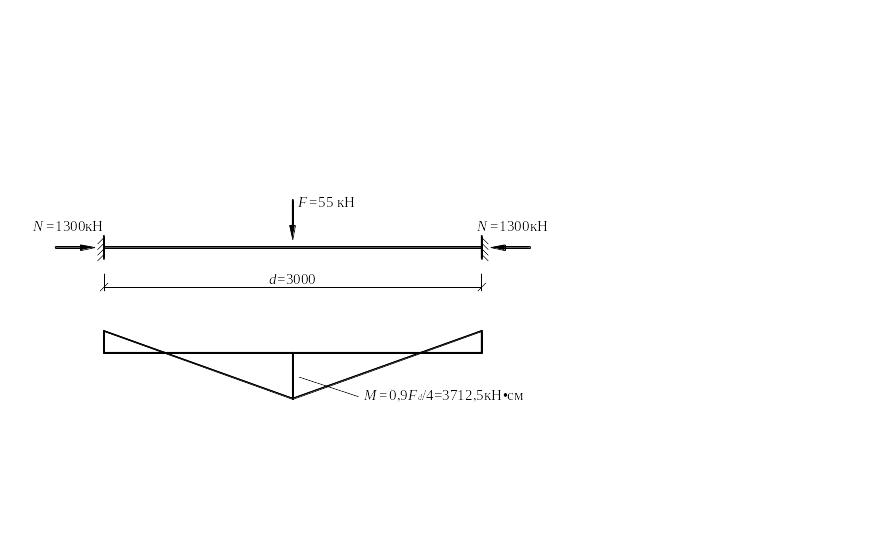
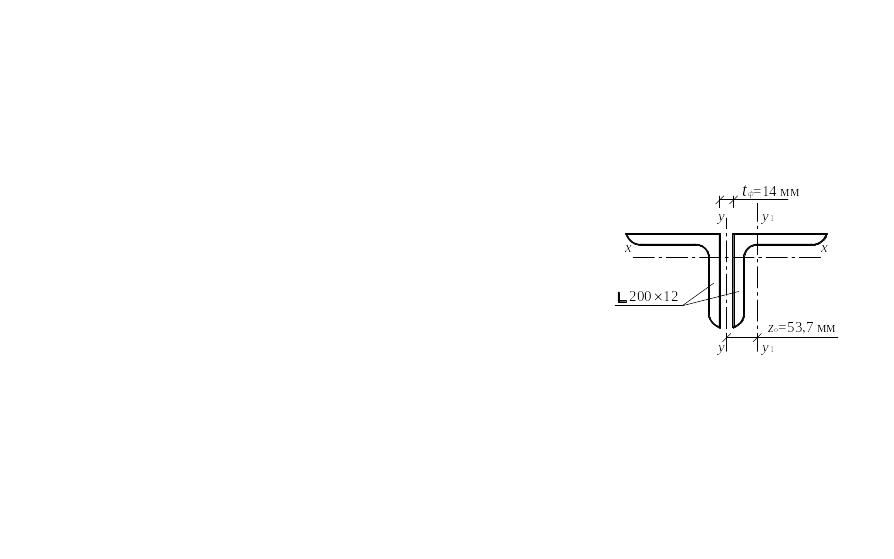
Рис.5.3. Расчетная схема и сечение пояса

Расчет на устойчивость сжато-изгибаемых элементов выполняется как в плоскости действия момента (плоская форма потери устойчивости), так и из плоскости действия момента (изгибно-крутильная форма потери устойчивости).

Расчет таких элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии, выполняется по формуле

N/(φ_еА) ≤ R_yγ_с.

При предварительном подборе сечения для поясов принимается гибкость λ = 60–90. Задаемся гибкостью λ_х = l_x/i_х = 60.

Определяем отвечающие этой гибкости и расчетной длине стержня l_x:

радиус инерции

i_x,тр = l_x/λ_x = 300 / 60 = 5 см;

требуемую высоту сечения

h = i_x/α₁ = 5 / 0,3 ≈ 17 см (принимаем h = 18 см),

где α₁ ≈ 0,3 для таврового сечения из двух равнополочных уголков (см. табл. 5.4);

ядровое расстояние

_x = W_c/A = (I_x/A)/z_о = i²_x/z_о = (0,3h)²/0,3h = 0,3h = 0,3 ∙ 18 = 5,4 см,

где z_о ≈ 0,3h – расстояние от центра тяжести до наиболее сжатого волокна для таврового сечения;

приведенный эксцентриситет

m_ef = ηe/ρ_x = 1,8 ∙ 2,86 / 5,4 = 0,95,

где η – коэффициент влияния формы сечения, определяемый по табл. 4.4 (для таврового сечения предварительно принимается η = 1,8);

условную гибкость

По условной гибкости и приведенному эксцентриситету m_ef из табл. 4.3 находим φ_е = 0,543.

Требуемая площадь сечения пояса

A_тр = N_n/(φ_еR_yγ_c) = 1300 ∙ 1 / (0,543 ∙ 24 ∙ 1) = 99,8 см²_.

По A_тр и i_х,тр из сортамента принимаем сечение из двух равнополочных уголков ∟200×12/ГОСТ 8510-86, имеющее характеристики:

А = 2 ∙ 47,1 = 94,2 см²; I_x = 2 ∙ 1822,78 = 3645,36 см⁴; i_х = 6,22 см; z_о = 5,37 см.

Определяем:

момент сопротивления сечения для наиболее сжатого волокна

W_c = I_x/z_о = 3645,56 / 5,37 = 678,88 см³;

ядровое расстояние

ρ_x = W_c/А = 678,88 / 94,2 = 7,2 см;

относительный эксцентриситет

m = e/ρ_x = 2,86 / 7,2 = 0,4;

гибкость

λ_х = l_x/i_х = 300 / 6,22 = 48,2;

условную гибкость

по табл. 4.4 при A_f /A_w = 1 и = 1,64 вычисляем

η = 1,8 + 0,12m = 1,8 + 0,12 ∙ 0,4 = 1,85;

приведенный эксцентриситет

m_ef = ηm = 1,85 ∙ 0,4 = 0,74.

По = 1,64 и m_ef = 0,74 определяем φ_е = 0,640.

Производим проверку устойчивости верхнего пояса в плоскости действия момента:

Резерв несущей способности 10,2%.

Несмотря на большое недонапряжение сечение принимается, так как изменение сечения в меньшую сторону (ближайший ∟180×12), приводит к перенапряжению стержня.

Проверяем устойчивость пояса фермы из плоскости действия момента, для чего определяем:

радиус инерции таврового сечения i_у = 8,7 (см. приложение В, табл. В.4);

момент инерции

I_y = i_y²A = 8,7² ∙ 94,2 = 7130 см⁴;

гибкость

λ_у = l_у/i_у = 300 / 8,7 = 34,5.

Так как гибкость стержня λ_у = 34,5 < λ_х = 48,2 (жесткость ЕI_y > EI_x), проверки устойчивости пояса из плоскости действия момента не требуется.

При ЕI_y < ЕI_x проверка устойчивости сжато-изогнутого пояса из плоскости действия момента производится по формуле

N/(cφ_yA) ≤ R_yγ_c,

где φ_y – коэффициент устойчивости при центральном сжатии относительно оси y-y, принимается по гибкости центрально-сжатого стержня λ_у;

с – коэффициент, учитывающий изгибно-крутильную форму потери устойчивости и зависящий от относительного эксцентриситета и формы сечения, принимается по [4, п. 9.2.4].

Пример 5.3. Подобрать сечение стержней растянутого нижнего пояса фермы по максимальному расчетному усилию в середине пролета N_max = 1300 кН и минимальному расчетному усилению в крайней панели N_min = 450 кН. Расчетная длина стержня в плоскости фермы l_x = 600 см.

Расчет на прочность элементов из стали с нормативным сопротивлением R_yn ≤ 44 кН/см² при центральном растяжении силой N выполняется по формуле

где A_п – площадь сечения элемента нетто с учетом возможных ослаблений отверстиями под болты или заклепки; для сварных конструкций A_п = А_вr.

Определяем требуемую площадь сечения нижнего пояса по максимальному усилию:

A_тр = N_max_n/(R_yγ_c) = 1300 ∙ 1 / (24 ∙ 1) = 54,17 см².

Принимаем сечение из двух неравнополочных уголков (ближайший номер проката)160×100×12, составленных узкими полками, (см. приложение В, табл. В.5). Площадь сечения А = 30,04 ∙ 2 = 60,08 см² > A_тр; радиус инерции стержня в плоскости фермы i_x = 2,82 см; i_y = 7,82; z_о = 2,36 см.

Проверяем прочность элемента:

Резерв несущей способности 9,8.

Проверяем гибкость (см. табл. 5.2):

в вертикальной плоскости

λ_х = l_x/i_х = 600 / 2,82 = 213 < λ_и = 400;

из плоскости фермы

λ_y = l_y/i_y = 1800 / 7,82 = 230 < λ_и = 400;

Определяем площадь сечения крайней панели нижнего пояса по минимальному усилию:

A_тр = N_min_n/(R_yγ_c) = 450 ∙ 1 / (24 ∙ 1) = 18,75 см².

Принимаем сечение их двух неравнополочных уголков 100×63×6, составленных узкими полками, с площадью сечения А = 9,59 ∙ 2 = 19,18 см²; радиус инерции i_x = 1,79 см; z_о = 1,42 см.

Проверяем прочность элемента:

Резерв несущей способности 2,2.

Проверяем гибкость в вертикальной плоскости:

λ_х = l_x/i_х = 600 / 1,79 = 335 < λ_и = 400.

Сечения удовлетворяют условиям прочности и жесткости.

Пример 5.4. Подобрать сечение сжатого среднего раскоса фермы по расчетному усилию N = –75 кН. Расчетные длины раскоса: из плоскости фермы l_y = l = 430 см; в плоскости фермы l_x = 0,8l = 0,8 ∙ 430 = 344 см (см. табл. 5.3).

Сечение средних малонагруженных элементов решетки фермы, как правило, подбирается по предельной гибкости λ_и.

Согласно табл. 5.1 для сжатого раскоса фермы λ_и = 210 – 60.

Принимаем минимальный коэффициент  = 0,5, тогда

λ_и = 210 – 60 ∙ 0,5 = 180.

Требуемые радиусы инерции:

при расчете в плоскости фермы

i_x,тр = l_x/λ_и = 344 / 180 = 1,91 см;

при расчете из плоскости фермы

i_у,тр = l_у/λ_и = 430 / 180 = 2,39 см.

По сортаменту принимаем сечение раскоса из двух равнополочных уголков ∟63×5, для которых i_x = 1,94 см > i_x,тр; i_y = 3,12 см > i_у,тр; площадь сечения А = 2 ∙ 6,13 = 12,26 см².

Гибкости стержня:

λ_x = l_x/i_x = 344 / 1,94 = 177 < λ_и = 180;

λ_у = l_у/i_у = 430 / 3,12 = 138 < λ_и.

Наибольшая условная гибкость раскоса

Коэффициент устойчивости при центральном сжатии согласно табл. 4.6  = 0,208.

Проверяем устойчивость центрально-сжатого раскоса:

где γ_c = 0,8 при λ > 60 (см. табл. 4.2).

Сечение стержня их двух уголков ∟63×5 не удовлетворяет условию устойчивости.

Принимаем сечение из 2∟75×5, для которых:

А = 2 ∙ 7,39 = 14,78 см²; i_x = 2,31 см; i_y = 3,57 см; z_о = 2,02 см;

Подсчитываем гибкости:

λ_х = l_x/i_x = 344 / 2,31 = 149;

λ_у = l_у/i_у = 430 / 3,57 = 120.

По наибольшей гибкости λ_max = λ_x = 149 определяем условную гибкость:

Коэффициент φ = 0,278.

Производим проверку раскоса:

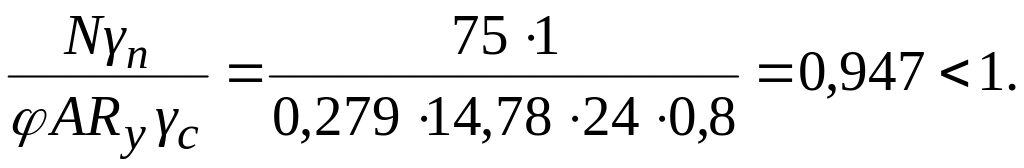
Степень загруженности элемента α = 0,947.