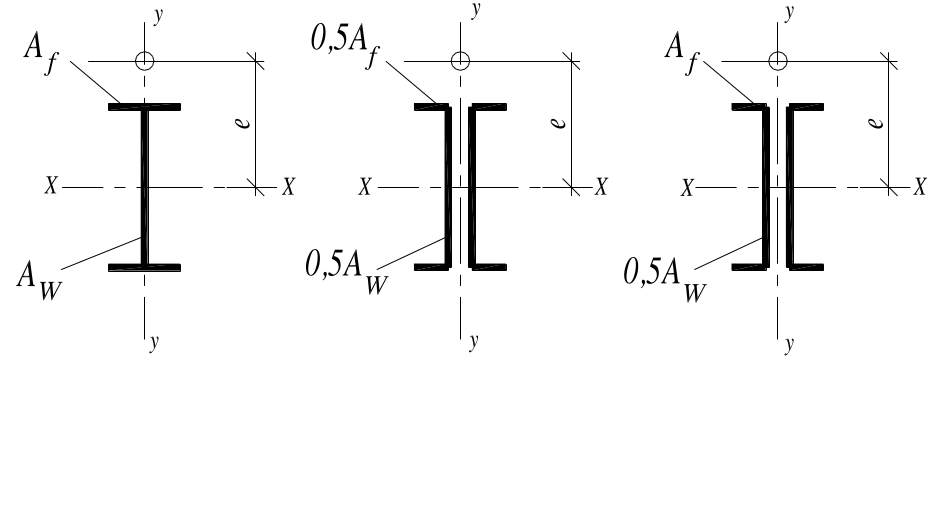- •Предисловие
- •1. Общие указания по содержанию и оформлению курсового проекта
- •2. Рекомендации по выбору конструктивной и расчетной схем каркаса
- •2.1. Разбивка сетки колонн
- •Схемы здания:
- •2.2. Компоновка однопролетной рамы производственного здания
- •Мостовые опорные краны нормального режима работы**
- •Основные размеры элементов подкрановых балок
- •2.3. Компоновка связей каркаса
- •Р ис. 2.4. Схема связей по колоннам
- •2.3.1. Связи между колоннами
- •2.3.2. Связи покрытия
- •3. Расчет поперечной рамы
- •3.1. Расчетная схема рамы
- •3.2. Нагрузки, действующие на поперечную раму
- •Назначение стали в конструкциях и сооружениях
- •3.2.1. Постоянные нагрузки
- •Нагрузки на прогон от веса ограждающих конструкций покрытия
- •Расчетное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли
- •Подкрановых балок нагрузками от колес мостовых кранов
- •3.2.2. Воздействия от мостовых кранов
- •3.2.3. Снеговая нагрузка
- •3.2.4. Ветровая нагрузка
- •Нормативные значения ветрового давления wo
- •Значение коэффициента kэ
- •3.3. Назначение жесткостей элементов рамы
- •3.3.1 Определение жесткости сквозного ригеля
- •3.3.2. Определение жесткостей ступенчатой колонны
- •3.4. Статический расчет поперечной рамы
- •3.4.1. Определение расчетных усилий в колонне
- •3.4.2. Определение расчетных сочетаний усилий
- •3.4.3. Выбор расчетных комбинаций усилий для подбора сечений верхней и нижней частей колонны
- •3.4.4. Определение расчетных усилий для расчета базы колонны, анкерных болтов и крепления фермы к колонне
- •3.5. Статический расчет стропильной фермы
- •3.5.1. Определение нагрузок на ферму
- •3.5.2. Определение усилий в стержнях фермы
- •Единичной узловой силы (б)
- •От единичного момента (б)
- •4. Расчет одноступенчатой внецентренно-сжатой колонны
- •4.1. Общие требования при проектировании конструкций
- •4.2. Исходные данные для расчета колонны
- •Коэффициент расчетной длины 1 для одноступенчатой колонны с верхним концом, свободным от закреплений
- •Коэффициенты условий работы с
- •4.3. Компоновка сечения и расчет надкрановой части колонны
- •Коэффициенты φe для проверки устойчивости внецентренно-сжатых сплошностенчатых стержней в плоскости действия момента
- •Коэффициент влияния формы сечения η
- •Коэффициенты для расчета на устойчивость центрально- и внецентренно-сжатых элементов
- •Значения коэффициентов α и β
- •4.3.1. Подбор сечения надкрановой части колонны
- •4.3.2. Проверка устойчивости надкрановой части колонны
- •4.3.3. Проверка местной устойчивости элементов сплошной колонны
- •Предельные условные гибкости
- •Минимальные катеты cварных швов k,min
- •4.4. Компоновка сечения и расчет подкрановой части колонны
- •Коэффициенты φe для проверки устойчивости внецентренно-сжатых
- •4.4.1. Подбор сечения ветвей колонны
- •4.4.2. Проверка устойчивости ветвей и стержня колонны в целом
- •4.4.3. Расчет крепления раскосов решетки к ветви колонны
- •Материалы для сварки, соответствующие стали
- •Нормативные и расчетные сопротивления металла швов сварных соединений с угловыми швами
- •Значения коэффициентов f и z
- •4.5. Расчет и конструирование базы внецентренно-сжатой сквозной колонны
- •4.5.1. Общие требования к базам колонн
- •4.5.2. Определение размеров опорной плиты в плане
- •Расчетные сопротивления бетона Rb
- •4.5.3. Определение толщины опорной плиты
- •Коэффициент 1 для расчета на изгиб плиты, опертой
- •4.5.4. Расчет траверсы
- •4.5.5. Расчет анкерных болтов и пластин
- •Расчетные сопротивления растяжению фундаментных болтов Rba
- •4.6. Расчет соединения надкрановой и подкрановой частей колонны
- •Расчетные сопротивления проката смятию торцевой поверхности
- •Расчетные длины стержней ферм lef
- •5.1.2. Выбор типов сечений стержней фермы
- •Приближенные значения радиусов инерции сечений
- •5.1.3. Подбор сечений элементов фермы
- •5.1.4. Примеры расчета и конструирования элементов стропильной фермы
- •Предельная гибкость
- •5.1.5. Расчет и конструирование узлов фермы
- •Подбор сечений элементов строительной фермы. Материал – сталь с245,
- •Расстояния между соединительными прокладками
- •5.1.6. Примеры расчета и конструирования узлов фермы
- •Значения коэффициента α
- •Максимальные катеты швов kf,max у скруглений
- •5.1.7. Сопряжение фермы с колонной
- •Расчетные сопротивления одноболтовых соединений срезу и растяжению болтов
- •Исходные данные для выполнения курсового проекта
- •Приложение б Исходные данные и результаты статического расчета поперечной рамы
- •Исходные данные для статического расчета рамы
- •Результаты статического расчета поперечной рамы (жесткое сопряжение ригеля с колоннами)
- •Обозначения: Мл, Nл, Qл – усилия в левой колонне; Мп, Nп, Qп – усилия в правой колонне.
- •Исходные данные для статического расчета рамы по программе
- •Результаты статического расчета поперечной рамы
- •(Вариант – шарнирное сопряжение ригеля с колоннами)
- •Правой колонне.
- •Сортаменты
- •Сталь широкополосная универсальная по гост 82-70*
- •Уголки стальные горячекатаные равнополочные по гост 8509-93 (выборка)
- •Продолжение таблицы в.4
- •Окончание таблицы в.4
- •Уголки стальные горячекатаные неравнополочные по гост 8510-86 (выборка)
- •Окончание таблицы в.5
- •Окончание таблицы в.6
- •Сталь горячекатаная, балки двутавровые по гост 8239-89
- •Продолжение таблицы в.8
- •Окончание таблицы в.8
- •Приложение г
- •Оглавление
- •Стальной каркас одноэтажного производственного здания
- •664074, Иркутск, ул. Лермонтова, 83
Значения коэффициентов α и β
Типы сечений |
Значения коэффициентов |
|||
a при |
b при |
|||
mx £ 1 |
1 < mx £ 5 |
|
> |
|
Открытые
|
0,7 |
0,65 + 0,05mx |
1 |
|
Обозначение,
принятое в табл. 4.7:
с
–
значение y
при
=
= 3,14![]() .
.
При
гибкости
![]() =
3,14 коэффициент
с
не должен превышать значений cmax,
определяемых согласно [4, прилож.
Д].
=
3,14 коэффициент
с
не должен превышать значений cmax,
определяемых согласно [4, прилож.
Д].
При определении относительного эксцентриситета mх за расчетный момент Mx для стержней с концами, закрепленными от смещения перпендикулярно плоскости действия момента, принимается максимальный момент в пределах средней трети длины, но не менее половины наибольшего момента по длине стержня.
4.3.1. Подбор сечения надкрановой части колонны
Для симметричного двутавра предварительно определяем значения характеристик:
радиуса инерции
ix = 0,42hв = 0,42 × 70 = 29,4 см;
радиуса ядра сечения
ρ = 0,35hв = 0,35 × 70 = 24,5 см;
гибкости стержня
![]()
условной гибкости
![]()
Эксцентриситет продольной силы
е = M2,max/N2 = 104700 / 760 = 138 см.
Относительный эксцентриситет
mх = е/ = 138 / 24,5 = 5,63.
Приведенный относительный эксцентриситет
mef = mx = 1,4 5,63 = 7,88,
где = 1,4 – коэффициент влияния формы сечения (для двутавра принимается в пределах от 1,2 до 1,7).
Требуемая площадь сечения:
Атр = N2n /(еRyc) = 760 × 0,95 / (0,152 × 24 × 1,05) = 188 см2,
где е = 0,152 – коэффициент устойчивости при внецентренном сжатии, определенный по табл. 4.3 при х = 2,19 и mef = 7,88.
Компоновка сечения. Распределяем площадь Атр между стенкой и полками.
Толщина стенки tw принимается в пределах:
(1/60–1/120)hw = 1,2–0,6 см,
где hw = hв – 2tf = 70 – 2 2 = 66 см (толщиной поясов предварительно задаются tf = 12–30 мм), задаемся tf = 20 мм.
Назначаем tw = 12 мм.
Требуемая площадь полки
Аf = bf tf = (Атр – hwtw)/2 = (188 – 66 1,2) / 2 = 54,4 см2.
Ширина полки
bf = Af /tf = 54,4 / 2 = 27,2 см.
Принимаем bf = 280 мм. Из условия жесткости bf обычно назначается в пределах bf = (1/20–1/30)l2 = (1/20–1/30) 6300 = 315–210 мм.
Окончательно проектируем стенку из листа 660×12 мм и полку из листа 280×20 мм. Рекомендуется размеры увязывать со стандартными размерами листов, выпускаемых отечественными заводами (см. приложение В, табл. В.3).
4.3.2. Проверка устойчивости надкрановой части колонны
Проверка устойчивости в плоскости действия момента (относительно оси х-х). Геометрические характеристики принятого сечения:
площадь стенки
Aw = hwtw = 66 1,2 = 79,2 см2;
площадь полки
Аf = bf tf = 28 2 = 56 см2;
площадь всего сечения
А = Aw + 2Af = 79,2 + 2 56 = 191,2 см2;
момент инерции
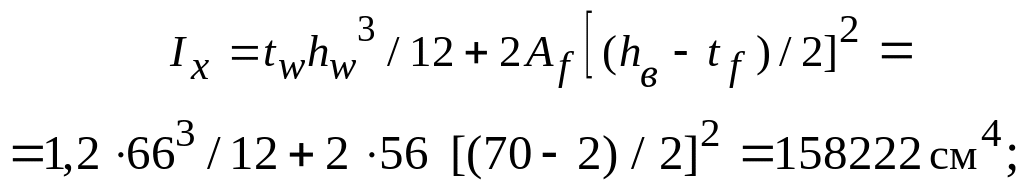
момент сопротивления для наиболее сжатого волокна
![]()
радиус инерции
![]()
гибкость стержня
![]()
условная гибкость
![]()
радиус ядра сечения
![]()
отношение Af /Aw = 56 / 79,2 = 0,7.
Относительный эксцентриситет
mх = е/ = 138 / 23,65 = 5,84.
При mх > 5 и Af /Aw = 0,5 коэффициент = 1,25;
при Af /Aw = 1 коэффициент = 1,4 – 0,02х = 1,4 – 0,02 2,24 = 1,36;
при Af /Aw = 0,7 по интерполяции = 1,29.
Приведенный относительный эксцентриситет
mef = mx = 1,29 5,84 = 7,53.
Производим проверку, сравнивая отношение расчетного усилия к несущей способности стержня колонны:
![]()
где е = 0,156 – коэффициент, определенный по табл. 4.3 при х = 2,24 и mef = 7,53.
Резерв несущей способности
![]()
что допустимо для составных сечений.
Проверка устойчивости из плоскости действия момента (относительно оси у-у). Во внецентренно-сжатых элементах, у которых жесткости в обоих главных направлениях различны (EIy < EIx) и момент действует в плоскости наибольшей жесткости, возможна потеря устойчивости в плоскости, перпендикулярной действующему моменту.
Геометрические характеристики сечения при работе стержня относительно оси у-у:
момент инерции сечения
![]()
радиус инерции
![]()
гибкость стержня
![]()
условная гибкость
![]()
При определении относительного эксцентриситета mх = (Mx/N2)/ за расчетный момент Mx принимается максимальный момент в пределах средней трети расчетной длины надкрановой части колонны (рис. 4.2):
М1/3 = M1 + 2(M2,max – M1)/3 =
= –417 + 2 [–1047 – (–417)] / 3 = –837 кН×м,
но не менее половины наибольшего по длине стержня момента:
Мх –M2,max/2 = –1079/2 = –539,5 кН×м.
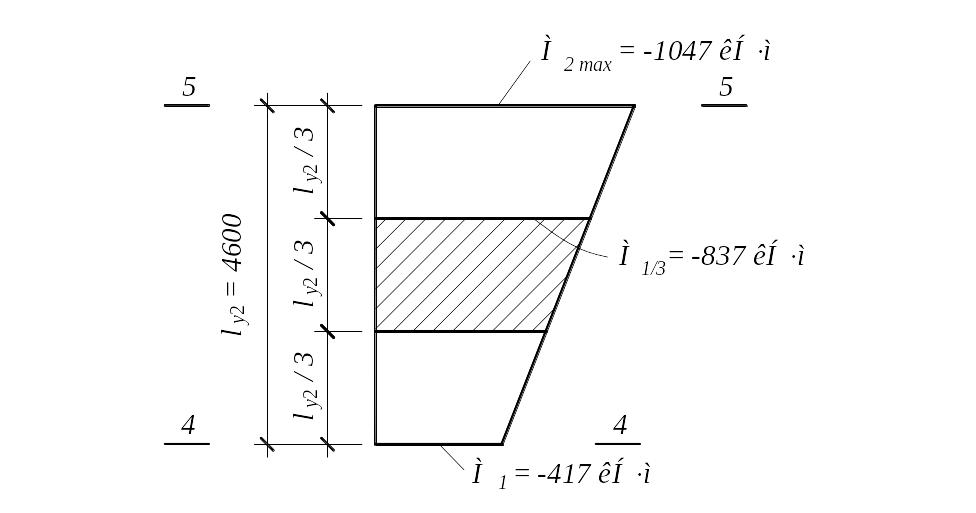
Рис. 4.2. Определение расчетного момента Мх
Здесь M1 определяется в сечении 4-4 при том же сочетании нагрузок, что и M2,max (1, 2, 4, 6, 8):
M1 = –220 – 142 + 41 –41 –55 = –417 кН.
Принимаем к расчету Мх = –837 кН×м.
Относительный эксцентриситет
mх = (М1/3/N2)/ = (83700/1047) / 23,65 = 3,38.
По табл. 4.5 определяем тип кривой устойчивости для двутаврового сечения – тип «в». По табл. 4.6 при условной гибкости y = 2,27 определяем коэффициент устойчивости при центральном сжатии y = 0,782.
Коэффициент, учитывающий влияние момента Mx при изгибно-крутильной форме потери устойчивости, при значениях относительного эксцентриситета mх < 5 определяем по формуле
с = /(1 + mх) = 1 / (1 + 0,82 3,38) = 0,27,
где = 1 при условии
y
= 66,5 <![]()
= 0,65 + 0,05mх = 0,65 + 0,05 3,38 = 0,82 при 1 < mx £ 5.
Проверку выполняем по формуле
![]()