1.2.2Использование методов оптимизации при планировании и анализе функционирования систем

Вторая важная область применения оптимизационных методов в инженерной практике связана с совершенствованием существующих систем и разработкой производственных планов для многопродуктовых технико-экономических процессов. Задачи анализа функционирования систем обычно возникают в тех случаях, когда требуется адаптировать существующую производственную систему к новым условиям функционирования, отличным от тех условий, которые были предусмотрены проектом этой системы. Причины, порождающие требования такого рода, как правило, связаны с не­обходимостью

1) увеличения общего объема выпуска продукции;

2) использования других видов сырья и расширения ассорти­мента изделий;

3) совершенствования технологических операций, отличающихся низким уровнем проектных решений.

В связи с решением указанных задач требуется выбрать новый температурный режим, давление или характеристики потока; установить дополнительное оборудование; разработать новые технологические операции. Методы оптимизации в производственном планировании ориентированы главным образом на составление программ производства нескольких видов продукции на отдельном предприятии, а также на координирование производственных планов предприятий, которые связаны хозяйственными отношениями. Поскольку в таких приложениях предполагается, что основное оборудование установлено и функционирует, предметом исследования являются только функции переменных затрат.

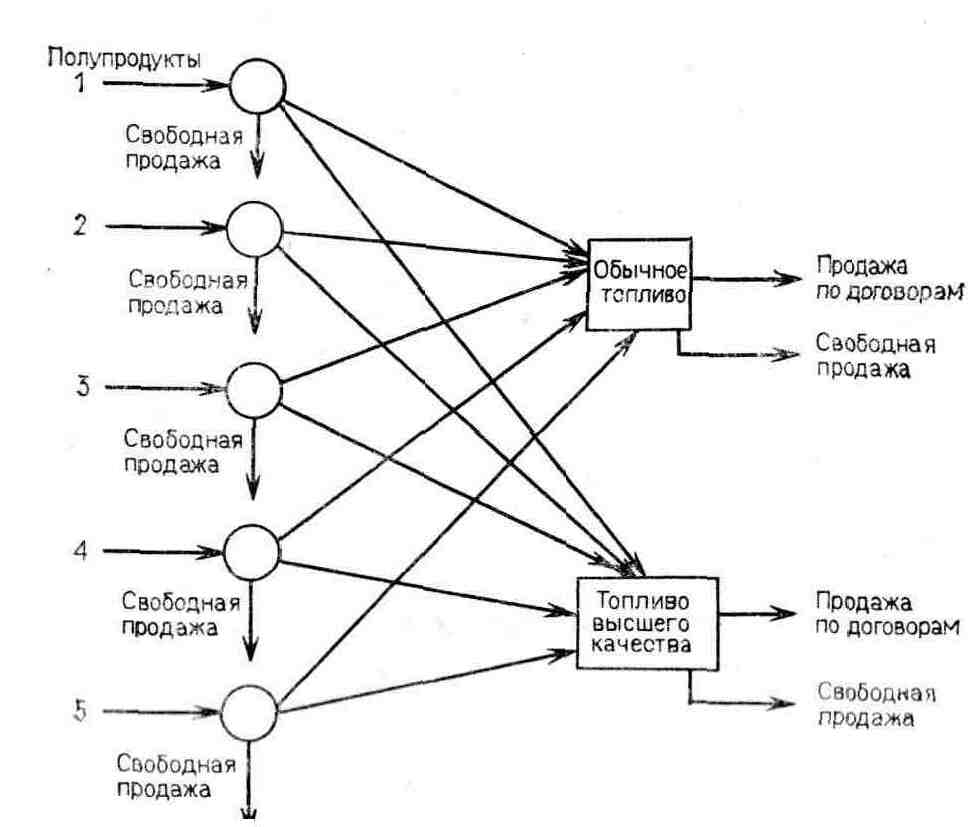
Рис. 1.5. Схема к задаче планирования нефтеперерабатывающего производства, пример 1.3.

Возникающие при этом задачи чаще всего можно сформулировать с помощью линейных и квазилинейных моделей. В качестве иллюстрации этого класса приложений оптимизационных методов рассмотрим задачу планирования производства нефтепродуктов.

Пример 1.3. Планирование производства нефтепродуктов

Описание задачи. В процессе переработки сырой нефти производится определенное количество бензиновых полупродуктов, которые затем последовательно смешиваются с целью получения двух видов топлива для двигателей внутреннего сгорания — обычного топлива и топлива высшего качества. Для каждого полупродукта известны значение показателя его эффективности, максимальный выход и фиксированная цена единицы объема полупродукта. Для каждого вида топлива установлены минимальное значение показателя эффективности и продажная цена, а также известны удельные затраты на смешивание топлива. Минимальный уровень производства обоих видов топлива определяется договорными обязательствами. Остальное произведенное топливо и неиспользованные полупродукты могут быть реализованы посредством свободной продажи по известным ценам. Требуется составить оптимальный план производства топлива в течение заданного периода времени.

Постановка задачи. На схеме, изображенной на рис.1.5, показано что исследуемая система включает ряд бензиновых полупродуктов, технологическую операцию смешивания и два вида жидкого моторного топлива. Процессы переработки нефти и производства полупродуктов исключены из рассмотрения наряду с подсистемами управления запасами и распределения сырой нефти, полупродуктов и конечной продукции. Поскольку оборудование, необходимое для выполнения операции смешивания, к началу планового периода установлено и функционирует, следует рассмотреть только стоимостные характеристики производственного процесса.

Характеристическим показателем качества функционирования системы в данном случае является чистая прибыль, реализуемая в течение планового периода. Чистая прибыль состоит из дохода от продажи топлива и полупродуктов за вычетом затрат на смешивание и производство полупродуктов. Независимые переменные выражают величины потоков по ориентированным дугам, изображенным на рис. 1.5. Таким образом, с каждым из полупродуктов ассоциированы три переменные. Одна из переменных выражает количество полупродукта, направляемого на производство обычного топлива, вторая — количество полупродукта, направляемого на производство топлива высшего качества, и третья — количество полупродукта, поступающею в свободную продажу.

Итак, для каждого полупродукта с номером i

х_i,— количество полупродукта, используемого для производства обычного топлива,

y_i— количество полупродукта, используемого для производства топлива высшего качества,

z_i— количество полупродукта, направляемого в свободную продажу.

С каждым видом производимого топлива в свою очередь ассоциированы две переменные, одна из которых представляет количество топлива, продаваемого по договорам, а другая — количество топлива, поступающего в свободную продажу.

Таким образом, для каждого вида топлива с номером j

и_j — количество топлива, продаваемого по договорам,

v_j — количество топлива, поступающего в свободную продажу.

В модель следует включить балансовые соотношения для каждого полупродукта и каждого вида топлива, ограничения, связанные с технологической операцией смешивания и позволяющие учесть заданные уровни эффективности двух видов топлива, а также ограничения, вытекающие из наличия договорных обязательств.

1. Балансовое соотношение для полупродукта с номером i записывается в виде неравенства

где — выход полупродукта i за плановый период.

2. Балансовые соотношения для конечной продукции имеют следующий вид:

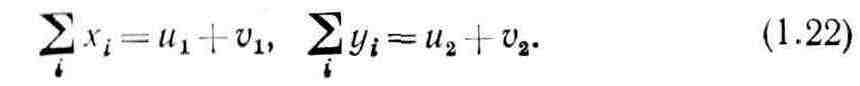
3. Технологические ограничения, связанные с операцией сме­шивания, записываются в виде

где ,— значение показателя эффективности полу продукта i, а — минимальное значение показателя эффективности топлива вида j.

4. Ограничение, обусловленное договорными обязательствами, для топлива вида j задается неравенством

где - минимальный объем производства топлива вида, предусмотренный договорами.

Характеристический показатель качества функционирование системы (чистая прибыль) определяется выражением

где продажная цена единицы конечной продукции вида j в соответствии с договорами; — рыночная цена единицы конечной продукции вида j; — рыночная цена единицы полупродукта i, — затраты на производство единицы полупродукта i. — технологические затраты на смешивание в расчете на единицу полупродукта i.

С учетом данных, приведенных в табл. 1.1, задача планирования принимает следующий вид:

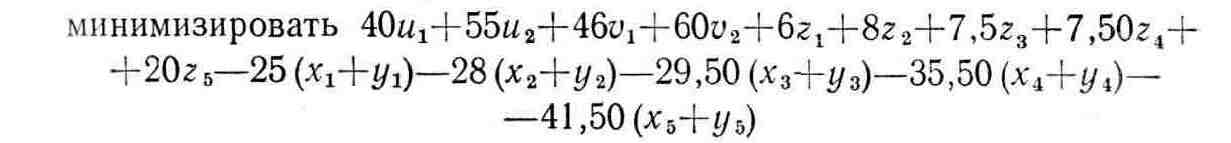
при следующих ограничениях:

ограничения типа (1.21):

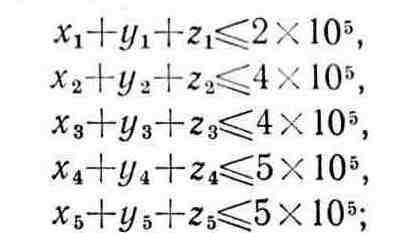
ограничения типа (1.22):

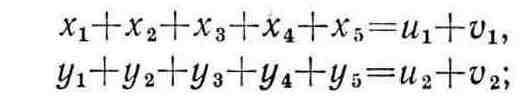
ограничения типа (1.23):

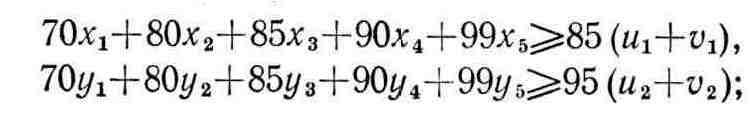
ограничения типа (1.24):

Кроме того, все переменные должны принимать неотрицательные значения; в противном случае решение задачи может и не иметь «физической» интерпретации. В целом задача оптимизации включает 19 переменных и 11 ограничений, а также условия неотрицательности переменных. Заметим, что все фигурирующие в модели функции являются линейными относительно независимых переменных.

Вообще говоря, в процессе нефтепереработки производится значительно большее количество различных полупродуктов и видов конечной продукции, чем это предполагалось в рассмотренном примере. Кроме того, в ряде практических ситуаций целесообразно ввести дополнительные переменные, отражающие динамику управления запасами, а также расширить модельные построения на несколько последовательных плановых периодов. В последнем случае каждая переменная должна быть снабжена вторым индексом, например:

— количество полупродукта i, используемое для производства обычного топлива в плановом периоде k.

При этом размерность результирующей модели производственного планирования существенно возрастает. На практике решение задач такого типа с числом переменных, превышающим тысячу, осуществляется на основе специальных алгоритмов.