2.5.3Метод секущих (хорд)

Метод секущих, являющийся комбинацией метода Ньютона и общей схемы исключения интервалов, ориентирован на нахождение корня уравнения в интервале (а, b), если, разумеется, такой корень существует.

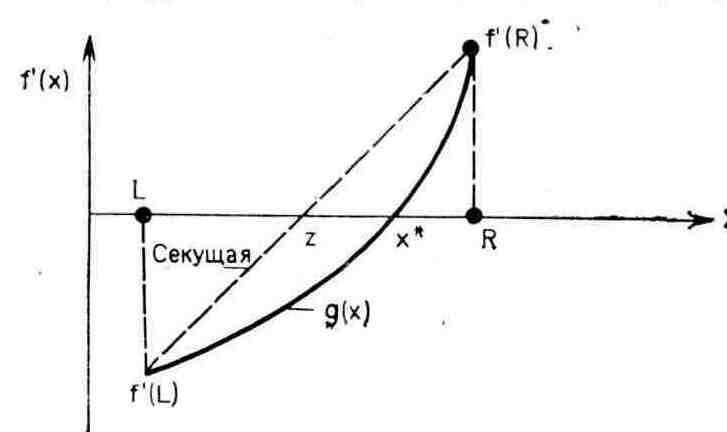
Рис. 2.20. Метод секущих

Предположим, что в процессе поиска стационарной точки функции f(x) в интервале (а, b) обнаружены две точки L и R, в которых знаки производной различны. В этом случае алгоритм метода секущих позволяет аппроксимировать функцию f'(x) «секущей прямой» (прямой линией, соединяющей две точки) и найти точку, в которой секущая графика f'(x) пересекает ось абсцисс (Рис. 2 .20). Таким образом, следующее приближение к стационарной точке определяется по формуле

Если , поиск следует закончить. В противном случае необходимо выбрать одну из точек L или R таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма. Например, в ситуации, изображенной на Рис. 2 .20, в качестве двух следующих точек должны быть выбраны точки z и R. Легко видеть, что в отличие от метода средней точки метод секущих основан на исследовании не только знака, но и значений производной в пробных точках и поэтому в ряде случаев позволяет исключить более половины интервала поиска (см. Рис. 2 .20).

Пример 2.11

Минимизировать функцию в интервале , используя Метод секущих

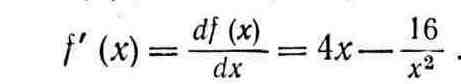
Итерация 1.

Шаг 1. .

Шаг 2

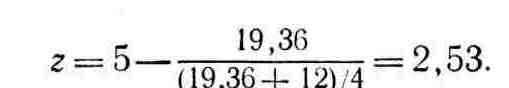
Шаг 3. ; положить R=2.53.

Итерация 2.

Шаг 2

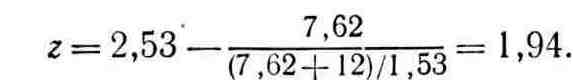
Шаг 3. ; положить R=1.94.

Итерации продолжаются до тех пор, пока не будет выполняться неравенство .

2.5.4Метод поиска с использованием кубичной аппроксимации

В соответствии с рассматриваемым методом подлежащая минимизации функция f аппроксимируется полиномом третьего порядка. Логическая схема метода аналогична схеме методов с использованием квадратичной аппроксимации. Однако в данном случае построение аппроксимирующего полинома проводится на основе меньшего числа точек, поскольку в каждой точке можно вычислять значения как функции, так и ее производной.

Работа алгоритма начинается в произвольно выбранной точке : находится другая точка , такая, что производные и имеют различные знаки. Другими словами, необходимо заключить стационарную точку , в которой , в интервал между и Аппроксимирующая кубичная функция записывается в следующем виде:

Параметры уравнения (2.8) подбираются таким образом, чтобы значения и ее производной в точках и совпадали со значениями f(x) и f'(x) в этих точках. Первая производная функции равна

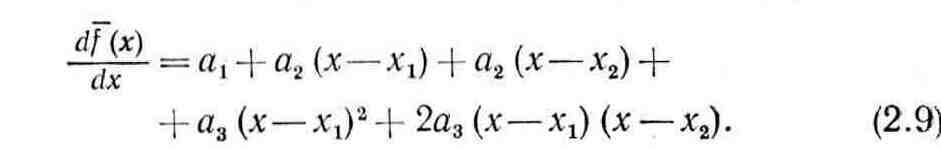
Коэффициенты из уравнения (2.8) определяются по известным значениям путем решения следующей системы линейных уравнений:

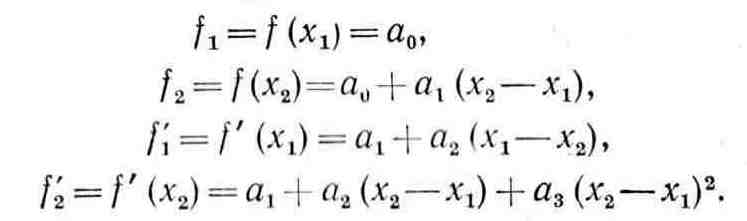
Заметим, что данная система легко решается рекурсивным ме­тодом. После того как коэффициенты найдены, действуя по анало­гии со случаем квадратичной аппроксимации, можно оценить коор­динату стационарной точки функции / с помощью аппроксимирую­щего полинома (2.8). При этом приравнивание к нулю производной (2.9) приводит к квадратному уравнению. Используя формулу для вычисления корней квадратного уравнения, запишем решение, определяющее стационарную точку аппроксимирующего кубичного полинома, в следующем виде:

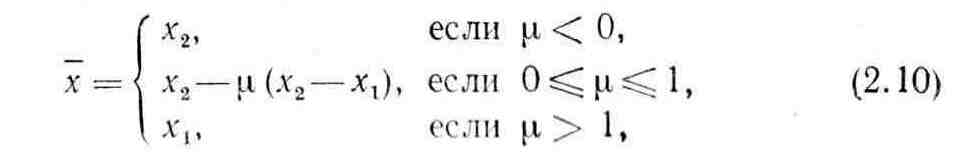
где

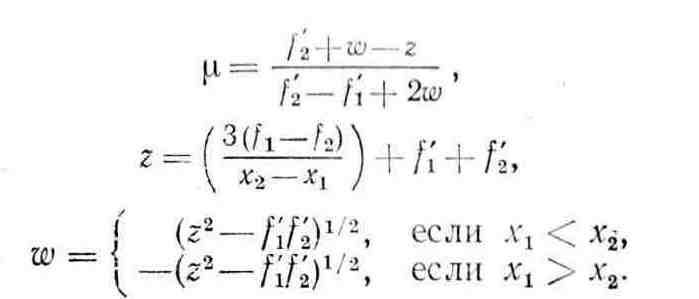
Формула для обеспечивает надлежащий выбор одного из двух корней квадратного уравнения; для значений , заключенных в интервале от 0 до 1, формула (2.10) гарантирует, что получаемая точка расположена между и . Затем снова выбираются две точки для реализации процедуры кубичной аппроксимации — ; и одна из точек или , причем значения производной исследуемой функции в этих точках должны быть противоположны по знаку. Процедура кубичной аппроксимации повторяется.

Приведем формализованное описание алгоритма. Пусть заданы начальная точка , положительная величина шага и параметры сходимости и .

Шаг 1. Вычислить .

Если , вычислить для значений k=0,1,2…

Если , вычислить для значений k=0,1,2…,

Шаг 2. Вычислить значения в точках при k=0,1,2…, вплоть до точки , в которой . Затем положить , . Вычислить значения .

Шаг 3. Найти стационарную точку аппроксимирующего кубичного полинома, пользуясь формулой (2.10).

Шаг 4. Если , перейти к шагу 5. В противном случае вычислять по формуле до тех пор, пока не будет выполняться неравенство .

Шаг 5. Проверка на окончание поиска.

Если и , поиск закончить. В противном случае положить либо

либо

затем перейти к шагу 3.

Заметим, что шаги 1 и 2 реализуют процедуру поиска границ интервала по эвристическому методу, причем изменение знака производной используется в качестве критерия перехода через точку оптимума. На шаге 3 проводятся вычисления координаты точки оптимума аппроксимирующего полинома. Шаг 4 ассоциирован с проверкой того факта, что полученная оценка действительно является улучшенным приближением к точке оптимума. В случае, когда значения производной вычисляются непосредственно, метод поиска с использованием кубичной аппроксимации, безусловно, оказывается более эффективным по сравнению с любым из представленных выше методов поиска. Однако если значения производной вычисляется путем разностного дифференцирования, то предпочтение следует отдать методу Пауэлла, основанному на квадратичной аппроксимации.

Пример 2.12

Минимизировать функцию , используя Метод кубичной аппроксимации и производных (начальная точка , длина шага , ).

Итерация 1.

Шаг 1. . Следовательно, .

Шаг 2. .

Так как , стационарная точка расположена между точками 1 и 2. Положим . Тогда .

Шаг 3.

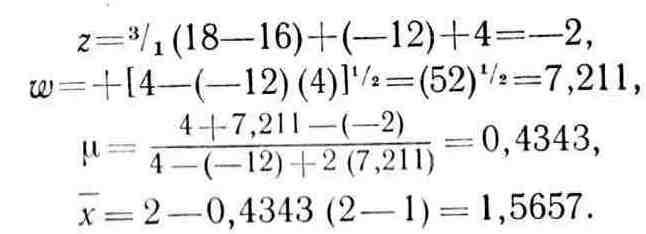
Шаг 4. . Следовательно, продолжаем поиск.

Шаг 5. Проверка на окончание поиска.

. Поиск не закончен, так как , положим

Итерация 2.

Шаг 3

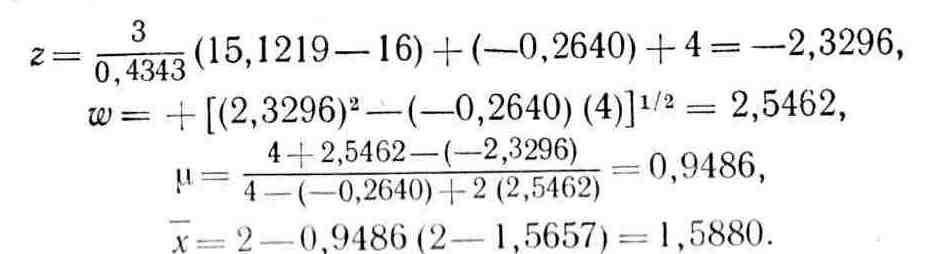
Шаг 4. . Следовательно, продолжаем поиск.

Шаг 5. Проверка на окончание поиска:

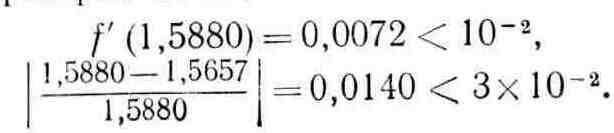
Поиск закончен.

Заметим, что при тех же самых исходных точках метод Пауэлла в примере 2.9 позволил получить оценку , тогда как метод с использованием кубичной аппроксимации привел к оценке . Точная координата точки минимума равна 1.5874, что указывает на преимущество полиномиальной аппроксимации более высокого порядка.