3. Максимизация прибыли фирмы в кратко- и долгосрочном периоде в различных рыночных структурах.

4. Основы теории потребительского поведения: полезность товара, кривые безразличия, бюджетные линии, оптимум потребителя.

Полезность товара, количественная и порядковая, предельная и общая.

Существует несколько способов оценки полезности товара:

1. Количественный, при котором вводят условные единицы полезности – ютили (от англ. utility). Такой подход к измерению полезности назван кардиналистическим.

2. Порядковый (ординалистический подход), основанный на упорядочении наборов товаров по предпочтениям.

При порядковом способе представления полезности используют несколько аксиом о свойствах отношений предпочтения и безразличия:

1. Сравнимость наборов (определены операции "<", ">" и "=").

2. Транзитивность отношений (если А > B, B > C, то и A > C).

3. Ненасыщенность – принцип "больше лучше, чем меньше".

Предельная полезность – полезность, извлекаемая из каждой дополни- тельной единицы блага (обозначение – MU от англ. marginal utility).

Совокупная (общая) полезность – сумма предельных полезностей (обозначение – TU от англ. total utility).

Пример. Рассмотрим, как меняются предельная и совокупная полезности с увеличением количества потребляемого товара (цена Р = 2 у.е.):

Q количество товара	TU совокупная полезность		MU предельная полезность
1	10	5	10	5
2	18	9	8	4
3	24	12	6	3
4	28	24	4	2
5	30	15	2	1

Закон убывающей предельной полезности и его влияние на спрос и цены.

Закон гласит: с увеличением количества приобретаемого товара падает его предельная полезность.

В соответствии с теорией потребительского выбора покупатель ведет себя так, чтобы максимизировать полезность при ограниченном доходе. При этом существуют два условия:

1. Полезность, приносимая последующей единицей товара, меньше полезности, приносимой предыдущей:

2. Потребитель стремится к достижению максимума общей полезности:

Потребитель всегда идет сначала от удовлетворения своих настоятельных потребностей (еда, одежда) к менее настоятельным.

Потребительский оптимум при количественном измерении полезности.

Оптимум потребителя определяется соответствием двум условиям:

1. Достижение максимальной совокупной полезности.

2. Полное использование дохода.

Правило максимизации полезности:

Максимальное удовлетворение потребности наступает при таком распределении дохода, когда последняя денежная единица, затраченная на при- обретение каждого вида продукта, приносила бы одинаковую предельную полезность:

Данная формула называется формулой потребительского оптимума, а со- отношение показывает, какая полезность приходится на одну затрачен- ную при покупке товара денежную единицу.

Задача. Найти потребительский оптимум при покупке двух товаров. Да-ны:

стоимость товара А – 1 у.е./шт,

стоимость товара В – 2 у.е./шт,

доход потребителя I – 10 у.е.

Единицы продукта	продукт A		продукт В
MUA		MUB
1	10	10	24	12
2	8	8	20	10
3	7	7	18	9
4	6	6	16	8
5	5	5	12	6
6	4	4	6	3
7	3	3	4	2

Решение. Потребительский оптимум можно найти двумя способами.

Первый способ. Будем рассматривать последовательность покупок в процессе достижения потребительского равновесия (т.е. до тех пор, пока ос- таток дохода не станет меньше цены самого дешевого товара):

№ шага	Возможности выбора		Принимаемое решение	Остаток дохода
1	первая единица А	10	первая единица В	10–2=8
первая единица В	12
2	первая единица А	10	первая единица А вторая единица В	8–1–2=5
вторая единица В	10
3	вторая единица А	8	третья единица А	5–2=3
третья единица В	9
4	вторая единица А	8	третья единица А четвертая единица В	3–1–2=0
четвертая единица В	8

Таким образом, получаем условие оптимума: I = 2A + 4B.

Второй способ.

1. Ищем равные значения в таблице по графам и отмечаем их.

2. Каждую пару проверяем, подсчитывая для нее значение TU:

первая единица А и вторая единица В: 10+24+20=54;

вторая единица А и четвертая единица В: 10+8+24+20+18+16=96;

четвертая единица А и пятая единица В: 10+8+7+6+24+20+18+16+12=121;

седьмая единица А и шестая единица В: 10+8+7+6+5+4+3+24+20+18+16+12+6=139.

3. Для каждой пары подсчитываем затраты на покупку I:

первая единица А и вторая единица В: 1+4=5;

вторая единица А и четвертая единица В: 2+8=10;

четвертая единица А и пятая единица В: 4+10=14;

седьмая единица А и шестая единица В: 7+12=19.

Отбрасываем пары, расходы по которым больше нашего дохода (10 у.е.) и берем ту пару, затраты по которой максимально близки к доходу (в нашем случае это пара 2А + 4В). Таким образом, снова получаем условие оптимума: I = 2A + 4B.

Полезность и доход. Условия оптимума потребителя при порядковом способе исчисления полезности.

Бюджетная линия – все сочетания товаров Х и Y, при которых общая сумма затрат равна доходу. Для каждой бюджетной кривой можно найти описывающее ее уравнение.

Пример. Вернемся к предыдущему примеру с едой и одеждой. Введем стоимость наших товаров: P_F = 1 у.е., P_C = 2 у.е. Составим таблицу:

Наборы товаров (точки на графике)	F	C	Расходы на покупку
A	0	40	40
B	10	15	40
C	20	10	40
D	30	5	40
E	40	0	40

В нашем случае бюджетная линия (ее уравнение: F + 2C = 40) будет выглядеть так:

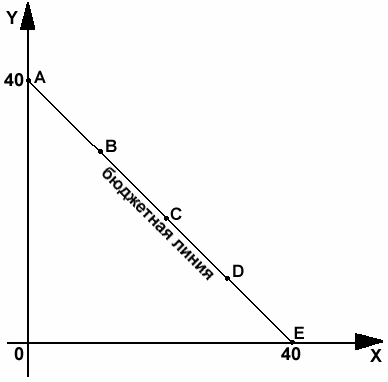
Рис. 14. Бюджетная линия.

В общем же случае уравнение бюджетной линии записывается в виде

Для удобства построения графика выразим отсюда Y:

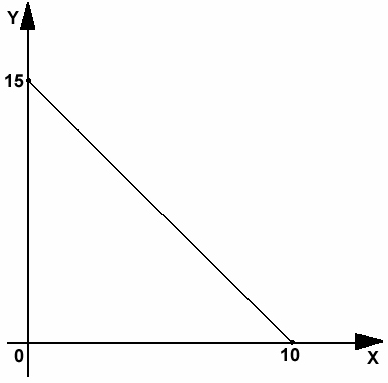
Задача. Имеется два продукта: Х – "Пепси-Кола", Y – лимонад. Цена лимонада P_Y = 12 у.е. Требуется найти: цену "Пепси-Колы" P_Х, доход

потребителя М и уравнение бюджетной линии.

Решение проведем в несколько шагов.

Шаг 1.

Определяем доход:

у.е.

Шаг 2.

Находим цену "Пепси-Колы":

у.е.

Шаг 3.

Найдем уравнение бюджетной линии:

Оптимум потребителя – наиболее эффективное использование денежных средств или покупка товаров, обладающих наибольшей полезностью. На рис. 15 точка касания A кривой безразличия и бюджетной линии и есть точка оп- тимума потребителя.

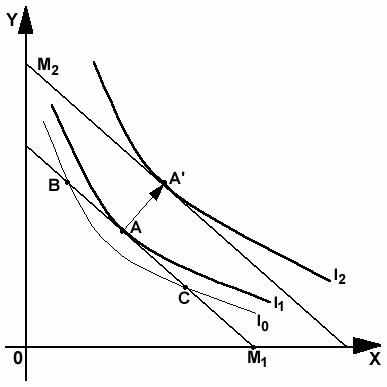
Рис. 15. Точка потребительского оптимума.

В этой точке потребитель расходует весь свой доход, максимально удовлетворяя при этом все свои потребности. У кривых I₀ и I₂ точек оптимума нет, а полезность наборов В и С меньше полезности набора А.

Условие потребительского оптимума при порядковом способе измерения полезности записывается в виде формулы

где отношение показывает угол наклона бюджетной линии.

Положение бюджетной линии может меняться под воздействием ряда факторов:

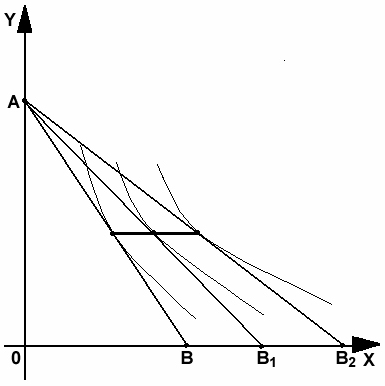1. И зменение дохода. цена – потребление

2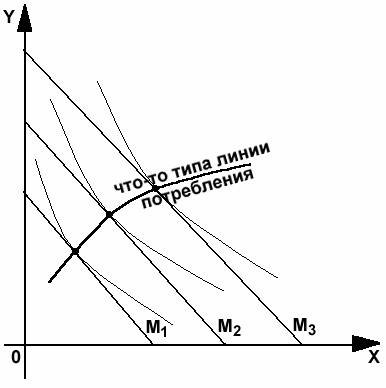 . Изменение цен на товары. доход – потребление