2. Сонячні елементи та батареї.

Сонячний елемент (фотогальванічний елемент, фотоелемент, фотоелектричний перетворювач) є приладом для перетворення світлової енергії у електричну, і таким чином є джерелом фото-е.р.с. Переважна їх більшість – наприклад ті, що використовуються в калькуляторах – є напівпровідниковими (кремнієвими) приладами з p-n переходом, тобто в своїй основі вони є напівпровідниковими діодами. Е.р.с. кремнієвого фотоелемента складає 0.5-0.7 В і мало залежить від його розмірів чи освітленості. Між тим максимальний струм, що може віддати сонячний елемент, прямо пропорційний світловій енергії, а вірніше падаючому потоку квантів світла. В ідеалі, всі падаючі кванти світла поглинаються і генерують рівну кількість фотоелектронів, які і створюють загальний фотострум. Порівняно з таким ідеальним випадком, сьогоднішні сонячні елементи мають ефективність 10-15%, а найкращі з них до 40%. Щоб підвищити вихідну напругу, сонячні елементи з'єднують послідовно, утворюючи сонячну батарею.

Н а малюнку – сонячно-електричне "дерево" в

в Штирії (Австрія).

.

.

Лабораторна робота 2-3

Вимірювання ємності конденсатора за допомогою фарадометра.

Мета роботи: ознайомлення з методом вимірювання ємності конденсатора за допомогою фарадометра, дослідження залежності ємності плоского конденсатора від відстані між його пластинами, визначення діелектричної проникливості діелектрика.

Обладнання: макет плоского конденсатора зі змінною відстанню між пластинами, набір діелектричних пластин різної товщини з різною діелектричною проникливістю, фарадометр - електронний прилад для вимірювання ємності.

Теоретичний вступ.

Якщо надати відокремленому провіднику деякий заряд , то він розподілиться по поверхні провідника так, що потенціал електростатичного поля в кожній точці поверхні буде однаковим (тобто поверхня стане еквіпотенціальною). Потенціал електростатичного поля залежить від: відстані від заряду , величини заряду , геометричної форми та розмірів тіла, діелектричної проникливості середовища, що оточує провідник. При збільшенні величини заряду провідника зростає і потенціал електростатичного поля на його поверхні, але відношення заряду до потенціалу є величиною сталою і називається електричною ємністю провідника, або просто ємністю.

Ємність визначається як коефіцієнт пропорційності між зарядом провідника і потенціалом електростатичного поля на його поверхні:

, (1)

тобто це та кількість електрики, яка може знаходитися на провіднику, якщо потенціал провідника дорівнює одиниці (якщо =1, то ).

Одиницею ємності є фарада (Ф): 1 Ф=1 Кл/В – це ємність такого тіла, потенціал поля якого змінюється на 1 В при наданні йому заряду в 1 Кл. Одна фарада – це дуже велика величина, таку ємність має куля радіусом 10¹⁰ м. На практиці вимірюють ємність в мікрофарадах (1 мкФ=10^-6 Ф), нанофарадах (1 нФ= 10^-9 Ф), пікофарадах (1 пкФ=10^-12 Ф).

Ємність првідника не залежить ні від величини заряду, ні від потенціалу на його поверхні, а залежить тільки від розмірів тіла, його форми та діелектричної проникливості оточуючого середовища (подібно як ємність посуду визначається тільки його розмірами). Крім того, наявність інших заряджених тіл, провідників або електричних полів також впливає на ємність, тому що внаслідок електростатичної індукції змінюється потенціал на поверхні даного провідника. Можна підібрати таку систему провідників, ємність якої є нечутливою до впливу зовнішніх тіл і полів. Така система називається конденсатором. Простим конденсатором є система з двох близько розташованих провідників, заряджених однаковими різнойменними зарядами.

Ємністю конденсатора називається відношення заряду, наданого провідникам, до різниці потенціалів на їх поверхнях

(2)

Плоский конденсатор - це дві близько розміщені однакові плоскі паралельні металеві пластини (обкладки), простір між якими заповнений діелектриком. Ємність плоского конденсатора визначається формулою:

(3)

де =8.85 *10^-12 Ф/м – електрична стала, - діелектрична проникність діелектрика, що знаходиться між пластинами конденсатора, - площа пластин, - відстань між ними.

Формула (3) визначає ємність ідеального конденсатора, який утворений двома нескінченими провідними пластинами, між якими електричне поле однорідне і існує тільки між пластинами. В реальному конденсаторі пластини не нескінчені, але якщо відстань між пластинами набагато менша від площі пластин ( ), то електричне поле в основному зосереджене між пластинами і можна користуватися формулою (3).

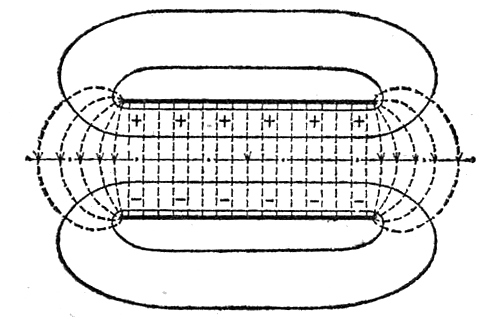
Мал. 1. Електричне поле плоского конденсатора:

еквіпотенціальні поверхні-суцільні лінії, лінії напруженості –штрихові лінії

У лабораторній роботі використовується макет плоского конденсатора, у якому відстань між пластинами достатньо велика і хоча електричне поле в основному локалізоване між пластинами, але поблизу країв поле виходить поза пластини і спричинює так званий ’крайовий’ ефект. Тому виміряне значення ємності буде відрізнятися від розрахованого за формулою (3) на величину . Це так звана ’паразитна’ ємність, вона зумовлена ’крайовим’ ефектом і ємністю з’єднувальних провідників. Отже, в результаті вимірювання отримаємо:

= (4)

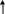
Мал. 2. Залежність виміряної ємності від .

Паразитну ємність можна визначити, побудувавши графік залежності виміряної ємності від оберненої відстані між пластинами. Продовживши цей графік до перетину з віссю , отримаємо як відстань між початком координат та точкою перетину графіка з віссю ординат.