
- •2. Теоретичні відомості
- •3.6 Статичний момент, приведений до валу двигуна
- •3. Програма роботи
- •4.Методичні вказівки по виконанню програми роботи
- •5.2 Мета роботи.
- •6. Додатки
- •Розрахунок спільної механічної характеристики
- •Вхідні дані до розрахунку
- •3. Розрахунок за допомогою системи matlab
- •3.1. Порядок виконуваних дій
- •3.2. Програма роботи
ЛАБОРАТОРНА РОБОТА №1
РОЗРАХУНОК СПІЛЬНОЇ МЕХАНІЧНОЇ ХАРАКТЕРИСТИКИ З ВИКОРИСТАННЯМ УНІВЕРСАЛЬНОЇ МАТЕМАТИЧНОЇ СИСТЕМИ MATLAB
1. Мета роботи
Вивчення методів розрахунку спільної механічної характеристики піднімального механізму і придбання навичок використання системи MATLAB для аналітичних розрахунків силових споживачів електричної енергії.
2. Теоретичні відомості
Метою даної роботи є розрахунок механізму підйому.
Механізм має кінематичну схему, показану на рис.1.
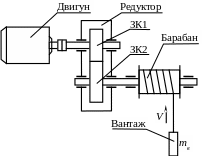 Рис.
1. Кінематична схема вантажного механізму
Рис.
1. Кінематична схема вантажного механізму
Вхідні данні:
1. Максимальна швидкість підйому вантажу — Vmax;
2. Маса вантажу — тв, кг;
3. ККД механізму — η;
4. Тривалість включення механізму — ТВ, %.
Послідовність розрахунку.
1. Ввод даних:
— максимальна швидкість підйому вантажу — Vmax;
— маса вантажу — тв, кг;
ККД механізму — η;
тривалість включення механізму — ТВ, %.
2. Вибір двигуна.
2.1 Статичний момент, приведений до валу двигуна

2.2 Потужність двигуна
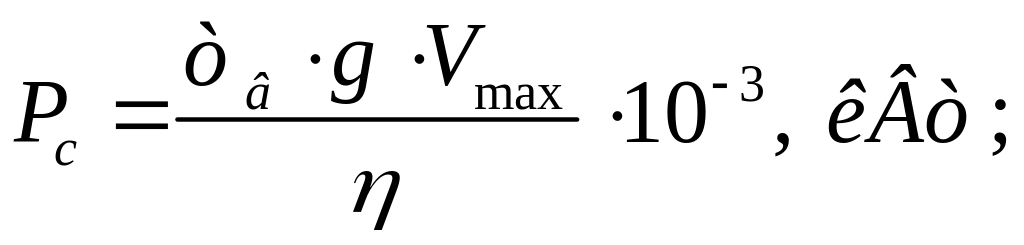
2.3 Потужність двигуна, приведена до стандартного значення ТВст

2.4 Обираємо двигун з
![]()
Паспортні данні двигуна:
— номінальна потужність при роботі в тривалому режимі Рном, кВт;
— номінальна частота обертання пном, об/хв;
— частота обертання магнітного поля статора пс, об/хв;
— максимальний момент двигуна Мmax, Н·м;
— маховий момент двигуна GD2, кг∙м2.
3. Перевірка двигуна на пуск.
3.1 Номінальний момент двигуна:
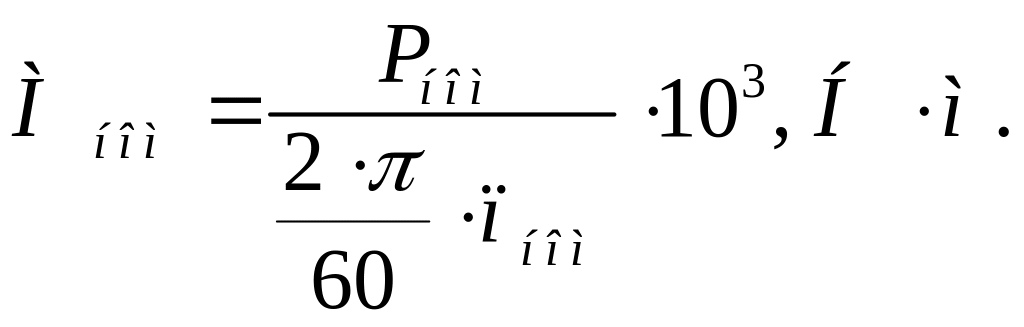
3.2 Перевантажувальна здатність двигуна:

3.3 Номінальне ковзання:

3.4 Критичне ковзання на природній характеристиці:
![]()
3.5 Пусковий момент двигуна

3.6 Статичний момент, приведений до валу двигуна
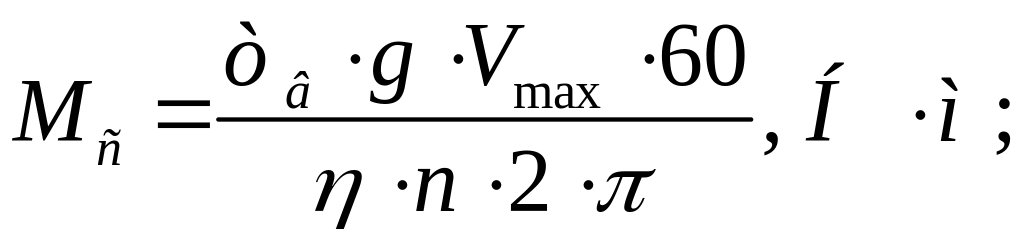
3.7 Перевірка двигуна згідно
умов пуску (![]() )
)
4 Будова спільної механічної характеристики
4.1 Критична частота обраного двигуна
![]()
4.2 Розрахунок спільної характеристики проводимо по формулі
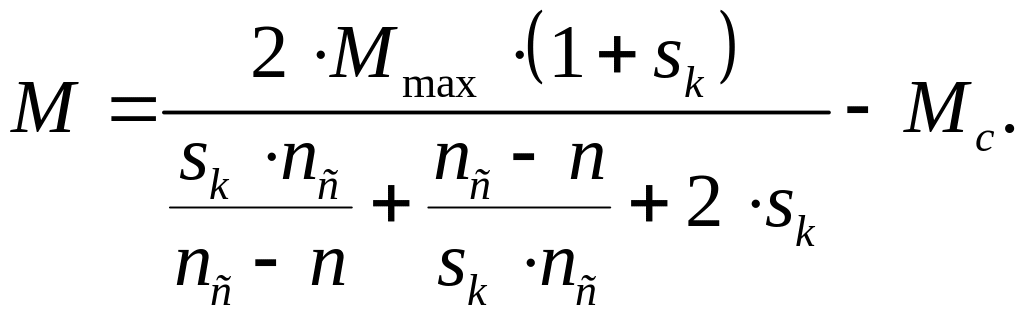
Результати розрахунку заносимо в таблицю 1.
4.3 Розраховуємо час пуску двигуна
час перехідного процесу на кожній ділянці визначаємо по формулі
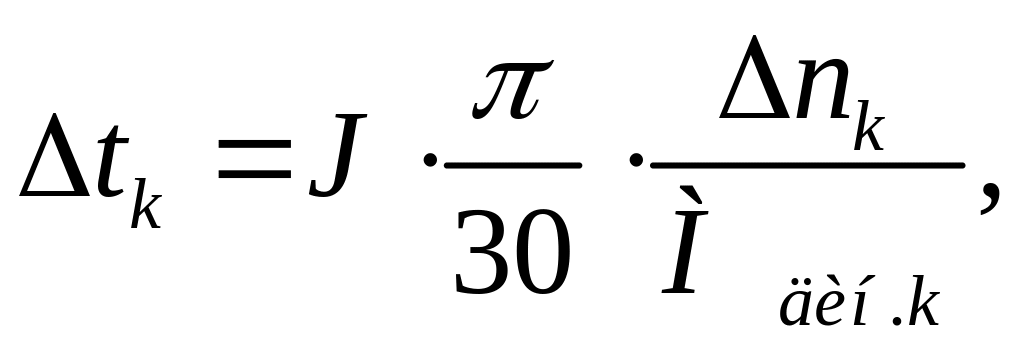
де
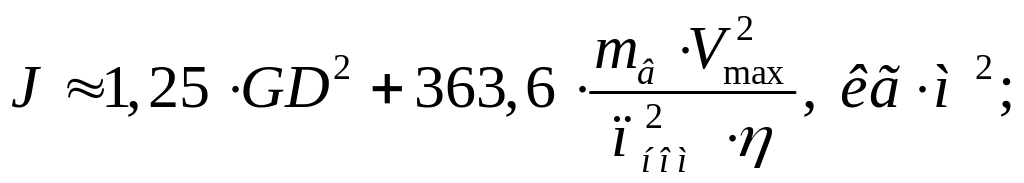
![]()
![]()
Результати розрахунку заносимо в таблицю 1.
Таблиця 1
n, об/хв |
|
|
|
|
|
|
|
|
|
|
|
|
M, Н·м |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
Δпk, об/хв |
|
|
|
|
|
|
|
|
|
|
|
|
Mдин.k, Н·м |
|
|
|
|
|
|
|
|
|
|
|
|
Δtk, c |
|
|
|
|
|
|
|
|
|
|
|
|
tпуск, с |
|
|
|
|
|
|
|
|
|
|
|
|
час пуску двигуна
![]()
Робота з програмою MATLAB
Система MATLAB, розроблена більше десяти років тому компанією MathWorks, є універсальним засобом для виконання математичних обчислень. Її робота заснована на виконанні операцій з матрицями, що й відбито в назві: MATLAB ― це скорочення від MATrix LABoratory (Матрична Лабораторія).
Дана система може використовуватися для розрахунків у багатьох галузях науки й техніки, таких як электро- і радіотехніка, динаміка, акустика, енергетика, економіка й т.п. MATLAB є незамінним помічником при виконанні матричного аналізу, при рішенні задач математичної фізики, статистичних, оптимізаційних і фінансово-економічних задач, при дослідженні й обробці сигналів і зображень, обробці й візуалізації інформації й т.д.
Однак найбільшою мірою система орієнтована на виконання інженерних розрахунків, оскільки її математичний апарат опирається на обчислення з матрицями й комплексними числами. MATLAB містить багато процедур і функцій, необхідних інженерові й науковцеві для виконання складних чисельних розрахунків і моделювання поводження технічних і фізичних систем.
Крім роботи із програмами, обчислення в середовищі MATLAB можна виконувати "у режимі калькулятора", тобто одержувати результат відразу ж після уведення потрібного оператора або команди.
Операції із числами
Як уже згадувалося в попередній главі, обчислення в середовищі MATLAB можна робити або в програмному режимі, викликаючи відповідну програму мовою MATLAB, що забезпечує уведення даних, виконання обчислень і висновок результатів, або "у режимі калькулятора", одержуючи результат відразу ж після уведення потрібного оператора або команди.
Робота "у режимі калькулятора" полягає в наступному. Користувач уводить у командне вікно підлягаючому обчисленню вираження, натискає клавішу <Enter>, після чого програма видає результат.
Програма MATLAB обчислила уведене вираження, а результат привласнила спеціальній змінній ans і вивела його в окремому рядку.
Крім того, під результатом з'являється новий знак запрошення (») з миготливим курсором, що говорить про те, що програма готова до уведення наступної команди.
Результат, збережений у змінній ans, можна використати для подальших обчислень. Так, якщо потрібно обчислити вираз (3 + 5)/2, наберіть у командному рядку вираження ans/2, натисніть клавішу <Enter>.
Найпростішим об'єктом мови MATLAB є число. Числа можуть бути цілими, дробовими, дійсними, комплексними, позитивними, негативними й т.д. Далі в цій главі будуть розглянуті правила уведення й обробки дійсних і комплексних чисел, векторів і матриць, а також найпростіші операції з ними.
Дійсні числа
Дійсні (речовинні) числа в системі MATLAB записуються в наступному виді.
0
1
-58
3.4576
0.00004
7.135е13
3.42е−3
Як прийнято в більшості мов програмування високого рівня, в MATLAB для відділення цілої частини числа від дробової в мантисі використається крапка, а не кома. А для відділення порядку числа від мантиси застосовується символ е ті запис 3.42е−3 відповідає запису 3.42×103, або 0.00342.
При цьому між символами в числах (зокрема між цифрами й символом е не повинно бути пробілів, інакше MATLAB видасть повідомлення про помилку.
Вид результату обчислень залежить від формату висновку, установленого в MATLAB. За замовчуванням використається формат short, при якому після десяткової крапки відображається чотири десяткові цифри.
Так, якщо в командний рядок увести число 8.48765326е−5 і нажати клавішу <Enter>, на екрані відобразиться наступне.
» 8.48765326е−005
ans =
8.4877е−005
Найпростіші арифметичні операції
З дійсними й комплексними числами в MATLAB можна проводити різні арифметичні операції, такі як додавання, вирахування, множення й ділення. Для цього в MATLAB, як й в інших мовах програмування, використаються традиційні арифметичні оператори: +, −, * й /. Є також оператор піднесення в степінь (^).
Порядок виконання арифметичних операцій такий.
1. Піднесення в степінь (^).
2. Множення й ділення (*, /).
3. Додавання й віднімання (+, −).
Іншими словами, серед арифметичних операторів найбільший пріоритет має оператор піднесення в степінь, а найменший - оператори додавання й віднімання. Виконання операцій однакового пріоритету відбувається в порядку ліворуч праворуч. Однак, використовуючи в математичних вираженнях круглі дужки, порядок виконання арифметичних операцій можна змінити.
Допустимо, потрібно знайти значення наступного арифметичного вираження.
(2.54×5.13 + 3.48)5 − (4.21 − 2.03)3
Для цього введіть дане вираження а командний рядок, використовуючи відповідні арифметичні оператори MATLAB, і натисніть клавішу <Enter>. Програма відобразить результат обчислень у вигляді значення системної змінної ans.
» (2.54*5.13+3.48)^5−(4.21−2.03)^3
ans =
1.2268е+006
Якщо потім знадобиться обчислити вираження, подібне представленому вище, наприклад
(2.54×5.13 + 3.48)5 + (4.21−2.03)3
те його зовсім не обов'язково вводити в командний рядок заново. C допомогою клавіш <↑> й <↓> й у рядку уведення можна відобразити раніше уведені із клавіатури команди й вираження. У цьому випадку скористайтеся клавішею <↑> - і в командному рядку відобразиться уведене вами на попередньому етапі вираження. Відредагуйте його потрібним образом і натисніть <Enter>.
» (2.54*5.13−3.48)^5+(4.21−2.03)^3
ans =
7.9687е+004
Щоб уникнути уведення дуже довгих і складних формул, використайте змінні для зберігання проміжних результатів.
Наприклад, розглянуте вище вираження можна обчислити в такий спосіб.
» а=(2.54*5.13−3.48)^5; » b=(4.21+2.03)^3; » с=а+b
с =
7.9687е+004
Зверніть увагу на те, що перші два рядки даного запису завершуються символом крапки з комою, що дозволяє уникнути виводу на екран результатів обчислення проміжних виражень, тобто виражень, привласнених змінним а й b.
