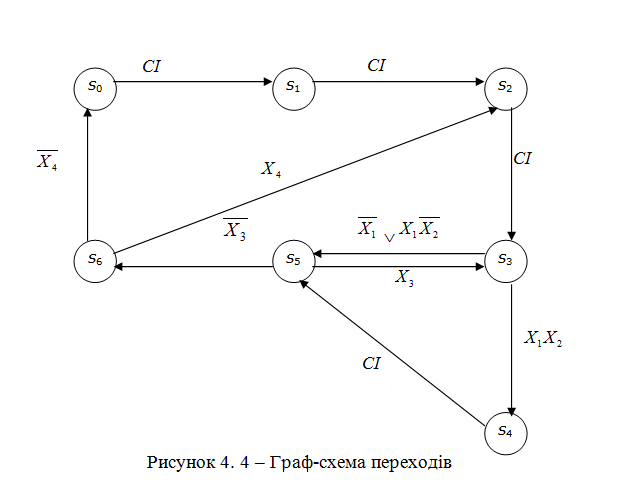
4.7. Побудова граф-схеми переходів

Граф-схема переходів (рис. 4.4) будується на основі закодованої мікрокомандної схеми алгоритму (рис. 4.3) і основної таблиці абстрактного автомата (табл. 4.3). Колами позначаються можливі стани автомата. Стрілки вказують на перехід із стану s_i до стану s_j. Над стрілкою вказується, під дією якого вхідного сигналу або сигналу СІ станеться перехід і який сигнал при цьому з’явиться на виході автомата.

4.8. Побудова системи рівнянь функцій переходів

Складаємо систему рівнянь функцій переходів (4.1). Ця система рівнянь складається на основі граф-схеми переходів (рис.4.4) або основної таблиці абстрактного автомата (табл. 4.3). Сигнал СІ в рівняннях не відображений. Наприклад, для першого рівняння системи правдивим є твердження, що можна перейти до стану s₀ зі стану s₆, якщо на вхід буде поданий сигнал . Шосте рівняння вказує на те, що можна перейти до стану s₅ зі стану s₄ під впливом синхроімпульсу або – зі стану s_3, якщо на вхід буде поданий сигнал або одночасно сигнали X₁ і . Таким чином, маємо (4.1):

(4.1)

Система рівнянь виходів для автомата Мура не будується.

4.9. Кодування внутрішніх станів автомата

Для того щоб закодувати внутрішні стани автомата, визначаємо кількість необхідних для цього тригерів (n). Кількість тригерів розраховується із співвідношення: log₂ S ≤ n, де n – кількість необхідних тригерів; S – кількість міток s_i (в прикладі s₀ – s₆)

S = 7, log₂ 7 ≤ n  n = 3.

Таким чином, необхідно мати 3 тригери. Тому внутрішні стани автомата будемо кодувати 3-розрядним двійковим кодом. Результати кодування наведені в табл. 4.4. У таблиці імена R₁–R₄ та S₁–S₄ – це входи трьох RS-тригерів.

Таблиця 4.4 – Кодування внутрішніх станів автомата

Стани	Входи
	R1	S1	R2	S2	R3	S3
s0	1	0	1	0	1	0
s1	1	0	1	0	0	1
s2	1	0	0	1	1	0
s3	1	0	0	1	0	1
s4	0	1	1	0	1	0
s5	0	1	1	0	0	1
s6	0	1	0	1	1	0

4.10. Побудова схеми операційного автомата

Операційний автомат (рис. 4.5) є керуючим пристроєм, результатом роботи якого є набір мікрооперацій. Мікрооперації mY_i подаються на вхід виконавчого пристрою, де вони виконуються. Виконавчий пристрій (в комп’ютері арифметично-логічний пристрій мікропроцесора) містить набір комбінаційних схем (суматори, регістри, лічильники, компаратори та інше), необхідних для виконання дій, пов’язаних з розв’язанням конкретної задачі. З виконавчого пристрою на вхід операційного автомата подаються сигнали з виходів компараторів X_і. Ці сигнали є вхідними сигналами операційного автомата і формують наступний стан автомата S_і.

Операційний автомат складається з трьох частин (рис. 4.5).

У вхідній частині розташовані три RS-тригери (Т₁-Т₃), які зберігають внутрішній стан автомата. Перед R-входом кожного тригера розташовано логічний елемент АБО. Подача одиничного сигналу на один із входів елементів АБО встановлює тригери в нульовий стан. Це дозволяє встановити автомат у початковий стан s₀. Також на входи R- і S- тригерів подаються сигнали, які є кодами станів автомата в поточний момент часу. Виходи RS-тригерів подаються на входи дешифратора. Дешифратор перетворює двійковий код внутрішнього стану автомата в одиничний сигнал на одному з виходів дешифратора. Виходи дешифратора є станами автомата в попередній момент часу S_t-1. Тип дешифратора вибирається залежно від кількості тригерів, які зберігають внутрішній стан автомата. Для даного прикладу використовується дешифратор на три входи.

Виходи дешифратора S_t-1 разом із виходами компараторів X_і подаються на вхід перехідної частини пристрою. На рис. 4.5 використане зображення двох загальних шин. На одну з цих шин подаються сигнали з виходів дешифратора. Наприклад, сигналу s_0t-1 припишемо нульовий номер. Оскільки маємо всього сім внутрішніх станів, то використаємо сім виходів дешифратора, позначених номерами від 0 до 6. На другу шину подаються виходи компараторів. Кожний компаратор відповідає одній умовній вершині. Оскільки в даному випадку є чотири компаратори з прямими та інверсними виходами, то на другу шину подаються вісім сигналів. Номеру 1 відповідає сигнал X₁, номеру 2 відповідає сигнал і т.д.

Перехідна частина будується на основі системи рівнянь для функцій переходів. Наприклад, для реалізації рівняння

потрібний логічний елемент І, на вхід якого необхідно подати шостий сигнал з першої шини, а саме s_6t-1, та восьмий сигнал з другої шини, а саме . Використавши такі рівняння, отримаємо перехідну частину автомата. Вихід перехідної частини подається на загальну шину St з сигналами, що є станами автомата в теперішній час.

У схемі автомата використані дві програмовані логічні матриці (ПЛМ) (рис. 3.8).

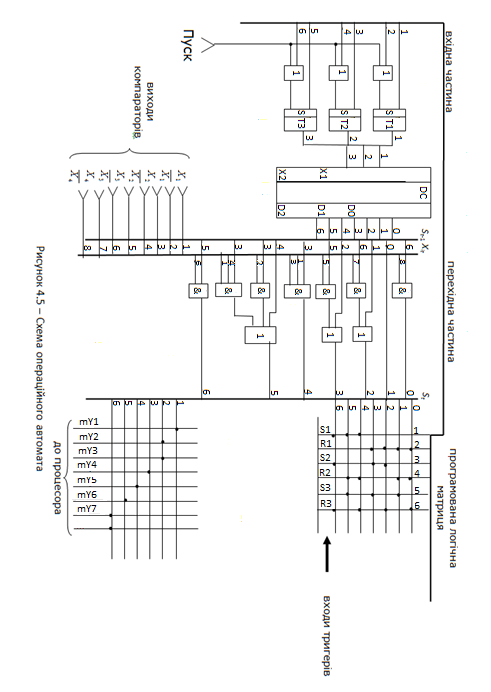
На рис. 4.5 верхня ПЛМ використовується для отримання вхідних сигналів для трьох RS-тригерів, а нижня – для отримання сигналів, що відповідають мікроопераціям, які має здійснювати виконавчий пристрій.

Сигнали, які відповідають станам St, подаються на входи верхньої ПЛМ. Виходами цієї ПЛМ є сигнали, які завдяки зворотному зв’язку подаються на входи RS-тригерів. Матриця програмується у відповідності до табл. 4.8. Так, якщо маємо одиничне значення стану s_0t, необхідно подати одиничний сигнал на R- входи всіх тригерів. Тому перетин горизонтальної лінії, позначеної номером 0, та вертикальних ліній, позначених номерами 2, 4 і 6 (ці лінії відповідають R- входам тригерів), позначаємо на схемі крапками. Таким чином, при одиничному сигналі для стану s_0t одиничний сигнал надійде на 2, 4 і 6 входи вхідної частини схеми автомата і встановить тригери в нульовий стан. Сигнал s_0t-1, пройшовши через перехідну частину пристрою, сформує стан s_1t, і цей сигнал надійде на перший вхід ПЛМ. Далі з 2, 4 і 5 виходів ПЛМ надійде на 2, 4 і 5 входи вхідної частини. Формування інших станів буде проходити аналогічно.

Вихідні стани автомата є станами автомата S_t в теперішній час. Вони подаються також на другу ПЛМ. Вона програмується у відповідності до табл. 4.6. Горизонтальні лінії цієї матриці асоціюються з мікрокомандами, а вертикальні – з мікроопераціями. Так, мікрокоманда Y_2t містить дві мікрооперації – mY₂ і mY₃. Тому перетин горизонтальної лінії, позначеної номером 2, та вертикальних ліній, позначених як mY2 і mY3, позначаємо крапками. Таким чином, при формуванні одиничного сигналу для вихідного стану Y2t сигнал надійде на необхідні входи процесора.