
- •Министерство науки образования
- •Теория автоматического управления
- •Техническое задание
- •Исходные данные
- •2. Выбор силовых элементов следящей системы
- •2.1 Выбор электродвигателя
- •2.2 Выбор преобразователя
- •2.3 Выбор трансформатора
- •2.4 Выбор дросселя
- •2.5 Вычисление коэффициентов передач и постоянных времени двигателя
- •2.6 Расчет коэффициента передачи тиристорного преобразователя
- •2. Синтез регуляторов следящей системы
- •2.1 Построение структурной схемы сс
- •2.1.1 Выбор и расчет элементов системы управления в контуре тока
- •2.1.2 Выбор и расчет элементов системы управления в контуре скорости
- •2.1.3 Определение структуры и параметров регулятора контура положения
- •2.1.4 Принципиальная схема регулятора
- •3. Оценка качества спроектированной системы
- •1. Техническое задание
2.1.2 Выбор и расчет элементов системы управления в контуре скорости
При
решении задачи синтеза регулятора
контура скорости, как правило, членом,
содержащим
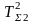 пренебрегают,
ввиду его малости. Тогда передаточная
функция контура будет:
пренебрегают,
ввиду его малости. Тогда передаточная
функция контура будет:

 .
.
Статическая ошибка по скорости на качественные показатели контура положения практически не влияет, поэтому в промышленных следящих системах, построенных по такому принципу, используют П – регулятор, что позволяет получить максимальное быстродействие контура. По той же причине фильтр в обратной связи по скорости исключают, тогда постоянная датчика скорости Тдс=0. Структурная схема контура скорости с учетом вышесказанного примет вид, приведенный на рис. 3.
Настройка контура тока, исходя из максимального быстродействия, выбирается таким образом, чтобы первая сопрягающая частота после частоты среза (ωс) была бы равна 2ωс, то есть:ωс=1/2Ткт или Краз=1/2Ткт («Оптимум по модулю»).
 .
.
Рис. 3 Структурная схема контура скорости
Схема контура скорости, соответствующая структурной схеме приведена на рис. 4.

Рис. 4 Схема контура скорости
Определим параметры схемы контура скорости (рис. 4 ). Сопротивления Rос, Rзс определяются из условия Rос/ Rзс=β1, при этом следует принять:
если <1, то Rос=1 ком, Rзс= 1/ β1 ком, ,
при β1>1 Rос= β1 ком, Rзс= 1ком, ,
где
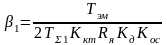
Поскольку
коэффициент передачи контура скорости
равен
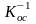 ,
то при максимальном напряжении на входе
системы (в аналоговых системах Uрс
max=10в)
ωн=10*К-1ос,
откуда получим Кос=10
/ ωн=10/157=0,064
,
то при максимальном напряжении на входе
системы (в аналоговых системах Uрс
max=10в)
ωн=10*К-1ос,
откуда получим Кос=10
/ ωн=10/157=0,064
Этот коэффициент образуется следующими элементами обратной связи: напряжением на зажимах тахогенератора Uтг, делителем R, фильтром в обратной связи по скорости Rфс и Сфс сопротивлением на входе регулятора Rс. тогда Кос= Ктг R Кс или , Кс= Кос / (R Ктг)
где Кс – коэффициент приведения обратной связи по скорости к задающему входу. С другой стороны Кс=Rзс / Rс из этого соотношения и определим величину сопротивления Rc.
Коэффициент передачи тахогенератора определить из соотношения

где Uтг- крутизна изменения выходного напряжения. Тахогенератор выбрать по максимальной скорости двигателя из таблицы 5.
Нам подойдет тахогенератор типа ТД-101
Напряжение возбуждения, 110±1,1 В
Ток возбуждения задается напряжением
Номинальная частота вращения 1500±15 об/мин
Активное сопротивление нагрузки 140±4 Ом
крутизна изменения выходного напряжения
19,98 ÷26,65 об/мин
Ктгmin=
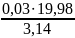 =0,19
=0,19
Ктгmax=
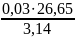 = 0,254
= 0,254
Свернем
контур скорости, тогда передаточная
функция контура скорости примет вид:


В
результате получим следующую структурную
схему контура положения:
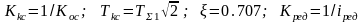
Кос=10 / ωн. = 10/157 = 0,06369
Ккс= 1/0,06369 = 15,87
Ткс = 0,0113 с
Кред = 1/146 = 0,0068
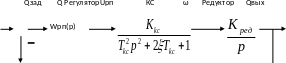
Рис. 5 Структурная схема следящей системы
Эта структурная схема является исходной для синтеза регулятора следящей системы.
2.1.3 Определение структуры и параметров регулятора контура положения
При решении задачи методом ЛЧХ последовательность решения задачи следующая:
Строим ЛАХ (
 )
разомкнутой нескорректированной
системы, предварительно приведя ее
к одноконтурной;
)
разомкнутой нескорректированной
системы, предварительно приведя ее
к одноконтурной;Строим желаемую ЛАХ (
 )
исходя из требований предъявляемых к
системе;
)
исходя из требований предъявляемых к
системе;ЛАХ регулятора получаем путем вычитания ЛАХ нескорректированной из ЛАХ желаемой
 .
.По
 получаем структуру и параметры
регулятора.
получаем структуру и параметры
регулятора.
Низкочастотная
часть ЛАХ
строится таким образом, чтобы обеспечить
точность отработки входного воздействия
при его известных предельных параметрах:
максимальной скорости
 ,
максимальном ускорении
,
максимальном ускорении
 и допустимой ошибке слежения
и допустимой ошибке слежения
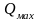 .
.
Закон изменения входного сигнала удобно представить в виде некоторого эквивалентного гармонического воздействия с заданными предельными характеристиками:

Тогда
 ,где
,где
 (7.1)
(7.1)
 ,
где
,
где
 (7.2)
(7.2)
Из
(7.1) и (7.2) можно получить
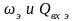 :
:

ωэ=
 =
0,58 Qвхэ
=
=
0,58 Qвхэ
=
 =
1,48
=
1,48
При оценке точности проектируемой системы на входе ее следует сформировать именно это воздействие.
Полученные параметры эквивалентного воздействия используются для построения так называемой «запретной зоны». Доказано, что ошибка слежения не будет превышена если ЛАХ системы пройдет выше запретной зоны (см рис.6).
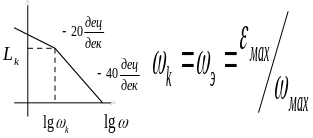 Qmax
= 0,0301 максимальная ошибка слежения дано
по условию
Qmax
= 0,0301 максимальная ошибка слежения дано
по условию
Lк
= 20lg ( )
=20lg 9,88 = 40
)
=20lg 9,88 = 40
ωэ = = 0,581 lg0,581 = -0,24
Рис. 6 Запретная зона
При
построении желаемой ЛАХ в среднечастотной
области необходимо руководствоваться
следующими соображениями: 1) она должна
пересекать ось 0 дец с наклоном -20 дец/дек
(на частоте среза
 );
2) протяженность среднечастотной области
по возможности должна быть как можно
продолжительной, обеспечение этого
условия позволяет минимально возможную
колебательность в системе. Высокочастотная
часть ЛАХ практически не оказывает
влияния на динамику системы при условии,
что
);
2) протяженность среднечастотной области
по возможности должна быть как можно
продолжительной, обеспечение этого
условия позволяет минимально возможную
колебательность в системе. Высокочастотная
часть ЛАХ практически не оказывает
влияния на динамику системы при условии,
что
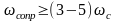 ,
где
,
где
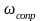 -
сопрягающая частота ближайшая справа
к частоте среза
-
сопрягающая частота ближайшая справа
к частоте среза
Найти структуру и параметры регулятора при следующих исходных данных:
Кkc=15,7;
Т=0.009;
 Кред=0,0055
Кред=0,0055
Qmax= 0.0301 -максимальная ошибка слежения
Ωmax 0.86 - максимальная скорость
εmax= 0.5 - максимальное ускорение
Предположим, что не заданы жесткие требований к виду процесса и быстродействию следящей системы. В этом случае можно построить желаемую ЛАХ следующим образом.
Построим запретную область
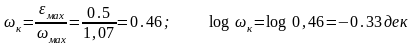

Вычисли
добротность системы по скорости ( ):
):

Определим
коэффициент усиления регулятора ( )
из следующего выражения:
)
из следующего выражения:
 ,
тогда
,
тогда

Сопрягающая частота для колебательного звена:
ω3=1/Tкс=1/0.0113=88,5,

Порядок построения желаемой ЛАХ
Строим запретную зону, используя следующие данные

Строим ЛАХ нескорректированной системы L(0)=20logKКред
и сопрягающая частота ω=ω3
3.
Сопрягающую частоту
 выбираем
таким образом, чтобы среднечастотный
участок желаемой ЛАХ был симметричным
относительно частоты среза, а
сопрягающую частоту справа от частоты
среза принимаем равной ω3.
выбираем
таким образом, чтобы среднечастотный
участок желаемой ЛАХ был симметричным
относительно частоты среза, а
сопрягающую частоту справа от частоты
среза принимаем равной ω3.
Все вышесказанное иллюстрируется на рис. 11
Низкочастотные
части нескорректированной (
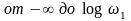 )
и желаемой (
)
и желаемой (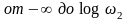 )
ЛАХ сливаются с границей запретной
зоны
)
ЛАХ сливаются с границей запретной
зоны
По
ЛАХ регулятора получим структуру и
параметры регулятора. Регулятор имеет
2 сопрягающие частоты
 .
При этих сопрягающих частотах ЛАХ
меняет наклон на 20 дец/дек (это говорит
о том, что регулятор содержит 2 звена
первого порядка: одно в знаменателе
(на частоте
.
При этих сопрягающих частотах ЛАХ
меняет наклон на 20 дец/дек (это говорит
о том, что регулятор содержит 2 звена
первого порядка: одно в знаменателе
(на частоте
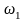 наклон меняется на – 20дец/дек) и одно в
знаменателе (на частоте
наклон меняется на – 20дец/дек) и одно в
знаменателе (на частоте
 наклон меняется на +20дец/дек). Таким
образом передаточная функция регулятора
будет иметь вид:
наклон меняется на +20дец/дек). Таким
образом передаточная функция регулятора
будет иметь вид:
 ,
где
,
где


Рис. 20 Иллюстрация синтеза регулятора методом ЛАХ
Полученные параметры регулятора могут уточняться, например, на основе моделирования системы.
