3 Пример расчета термодинамических свойств
Пример. Определить тепловой эффект, изменение изобарно изотермического потенциала, константу равновесия и равновесную степень превращения для реакции:
С5Н12 С2Н4+С3Н8
в интервале температур от 298 до 1200 К и давлениях Р1 = 0,1; Р2 = 2 МПа,
Р2 = 4 МПа
Необходимые данные для расчета берутся из таблицы 1 и 2 приложения.
Приведем подробный пример расчета при температуре 800 К и давлениях 0,1, 2 МПа.
Тепловой эффект при стандартных условиях составит:
=
52,30-103,85+146,44 = 94,89 кДж/моль=94890 Дж/моль.
Аналогично
рассчитываются ∆СР,
∆СР= 43,56+73,51-120,21= -3,14 Дж/(моль∙К);
=
219,45+269,91-348,95 = 140,41 Дж/моль;
∆а = 11,32+1,72-6,9 = 6,14;
∆b = (122,01+270,75-425,93)∙10-3 = -33,17∙10-3;
∆с = (-37,90-94,48+154,39)∙10-6 = 22,01∙10-6.
Тепловой эффект по грубому уравнению Кирхгофа при 800 К рассчитывается по уравнению (5).
=
94890+6,14∙(800-298) = 93314,2 Дж/моль.
Тепловой эффект по точному уравнению Кирхгофа при 800 К рассчитывается по уравнению (13).
= 94890+6,14∙(800-298)-33,17·10-3∙(8002- 2982)/2+22,01∙10-6∙(8003- -2983)/3 = 92393,2 Дж/моль.
Энергию Гиббса по грубому уравнению рассчитывают по уравнению (21).
=
94890-800∙140,41 = -17438,0 Дж/моль.
Энергию Гиббса по приближенному уравнению рассчитывают по уравнению (25).
=
94890-800∙140,41+3,14∙800∙0,3597 = -16534,4 Дж/моль.
Энергию Гиббса по точному уравнению рассчитывают по уравнению (26).
=94890-140,41∙800-800∙(6,14∙0,3597-33,17∙10-3∙0,1574∙103+22,01∙10-6 0,0733∙106) = -16318,7 Дж/моль.
Константу равновесия при 800 К и 0,1 МПа рассчитывают по уравнению (32).
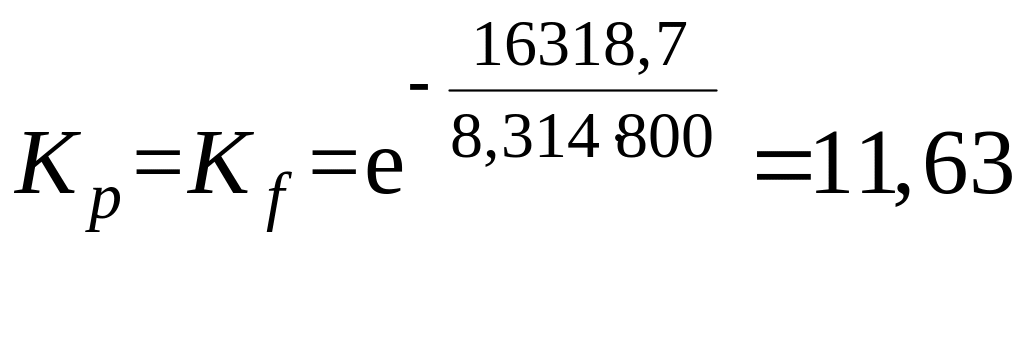
Константу равновесия при 800 К и 2,0 МПа рассчитывают по уравнению (36). Для этого вычисляют приведенную температуру и давление для каждого реагента.
Для
С2Н4
=
800/282,4 = 2,83;
=
2/5,04 = 0,40;
С3Н8 = 800/370 = 2,16; = 2/4,26 = 0,47;
C5H12 = 800/469,8 = 1,70; = 2/3,37= 0,59.
Коэффициент активности определяют по графику (см. рисунок приложения).
= 1,0;
= 1,0;
= 1,0.
Рассчитывают Ку по уравнению:
.
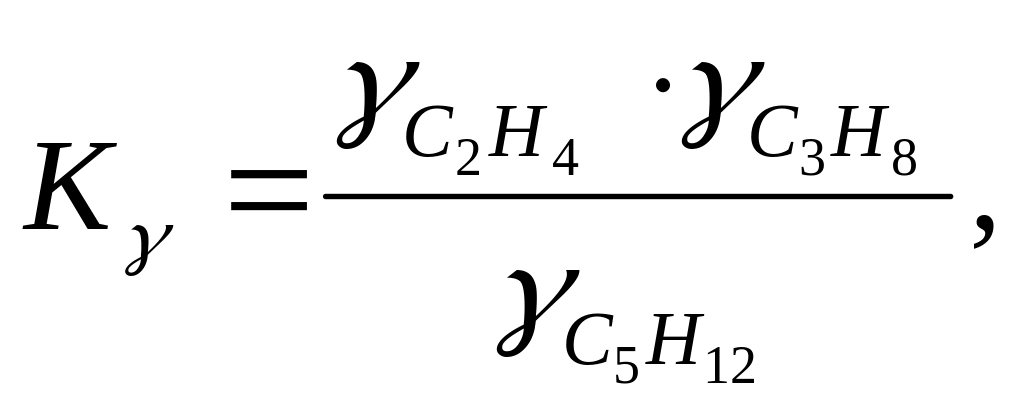
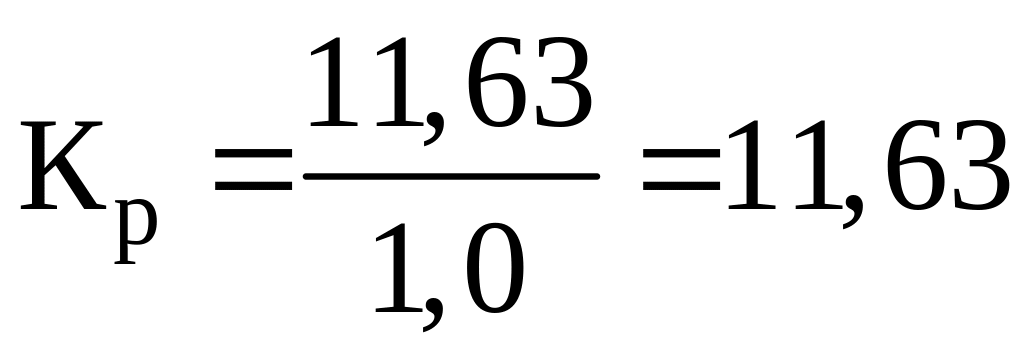Равновесную степень превращения исходных веществ рассчитывают по уравнению (45).
При 0,1 МПа
При 2 МПа
Для остальных давлений и температур расчет ведется аналогично, результаты расчета сведем в таблицу 1. По результатам расчета построим вышеуказанные графические зависимости (рисунки 1, 2, 3).
Таблица 1 – Сводная таблица термодинамических величин
Т,К |
∆Нгр, Дж/моль |
∆Нточ, Дж/моль |
∆Gгр, Дж/моль |
∆Gпр, Дж/моль |
∆Gточ, Дж/моль |
Кp |
Кγ |
КP |
Х |
||||
2 МПа |
4 МПа |
2 МПа |
4 МПа |
0,1 МПа |
2 МПа |
4 МПа |
|||||||
298 |
94890,0 |
94889,6 |
53047,5 |
53047,8 |
53019,7 |
5,2∙10-10 |
1,15 |
0,40 |
4,5∙10-10 |
1,3∙10-9 |
0,0000 |
0,0000 |
0,0000 |
400 |
94570,3 |
94610,9 |
38726,0 |
38775,2 |
38763,7 |
8,7∙10-6 |
1,20 |
0,58 |
7,2∙10-6 |
1,5∙10-5 |
0,0029 |
0,0006 |
0,0006 |
500 |
94256,3 |
94179,8 |
24685,0 |
24862,8 |
24848,9 |
2,5∙10-3 |
1,18 |
0,66 |
2,2∙10-3 |
3,8∙10-3 |
0,0503 |
0,0104 |
0,0098 |
600 |
93942,3 |
93637,1 |
10644,0 |
11013,6 |
11032,2 |
1,1∙10-1 |
1,09 |
0,83 |
1,1∙10-1 |
1,3∙10-1 |
0,3142 |
0,0708 |
0,0572 |
700 |
93628,3 |
93026,8 |
-3397,0 |
-2783,1 |
-2687,7 |
1,6 |
1,05 |
0,95 |
1,2∙101 |
1,5 |
0,7832 |
0,2648 |
0,2002 |
800 |
93314,3 |
92392,9 |
-17438,0 |
-16534,7 |
-16318,0 |
1,2∙101 |
1,00 |
1,00 |
1,2∙101 |
1,2∙101 |
0,9596 |
0,6063 |
0,4746 |
900 |
93000,3 |
91779,5 |
-31479,0 |
-30247,0 |
-29869,7 |
5,4∙101 |
1,00 |
1,00 |
5,4∙101 |
5,4∙101 |
0,9909 |
0,8546 |
0,7584 |
1000 |
92686,3 |
91230,6 |
-45520,0 |
-43924,3 |
-43356,1 |
1,8∙102 |
1,00 |
1,00 |
1,8∙102 |
1,8∙102 |
0,9973 |
0,9497 |
0,9063 |
1100 |
92372,3 |
90790,2 |
-59561,0 |
-57570,1 |
-56792,4 |
5.0∙102 |
1,00 |
1,00 |
5.0∙102 |
5.0∙102 |
0,9990 |
0,9805 |
0,9621 |
1200 |
92058,3 |
90502,3 |
-73602,0 |
-71187,4 |
-70195,0 |
1,1∙103 |
1,00 |
1,00 |
1,1∙103 |
1,1∙103 |
0,9996 |
0,9913 |
0,9829 |
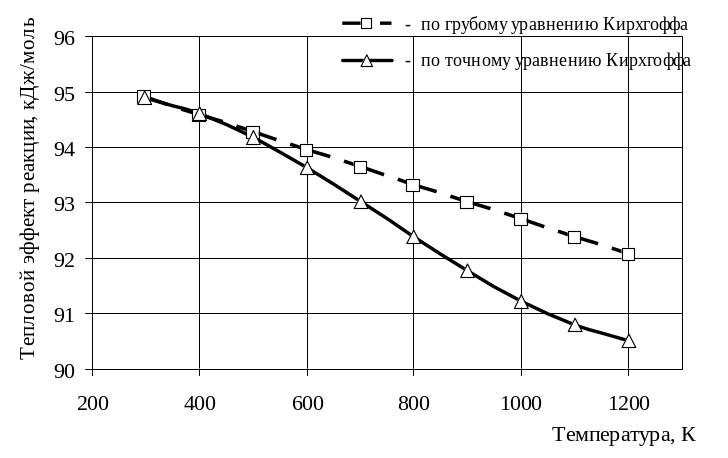
Рисунок 1 – Графическая зависимость теплового эффекта химической реакции от температуры, вычисленного по грубому (5) и точному (13) уравнениям Кирхгоффа
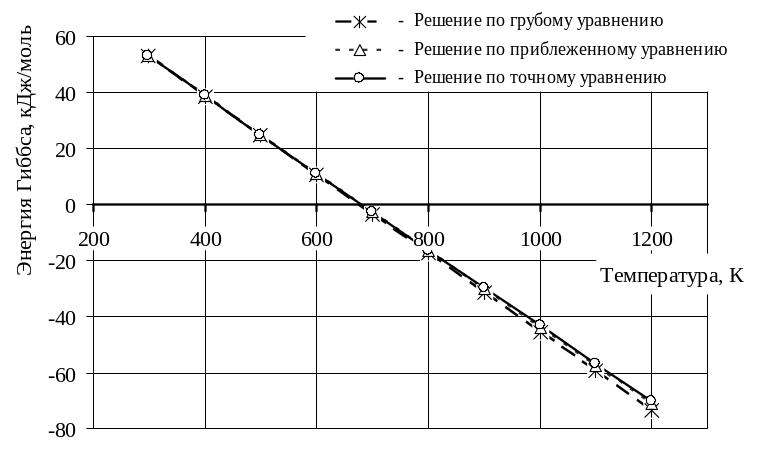
Рисунок -2 – Графическая зависимость изобарно-изотермического потенциала от температуры, вычисленного по уравнениям грубому (21), приближенному (25) и точному (26)
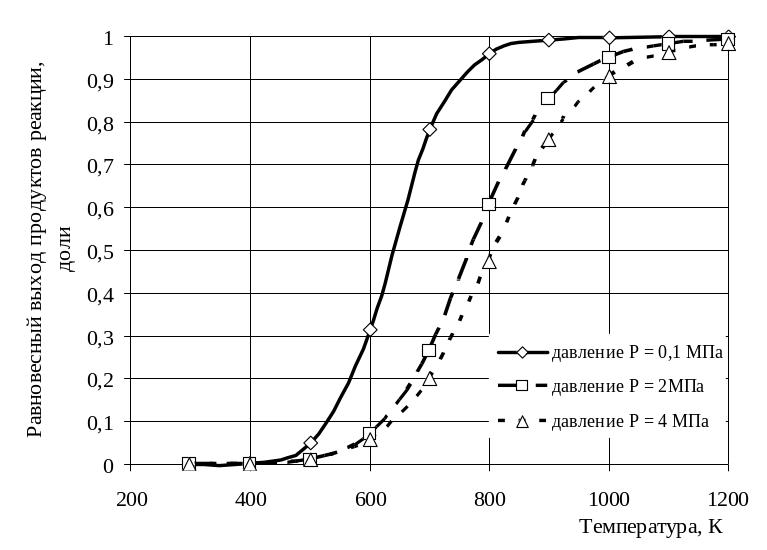
Рисунок 3 – Графическая зависимость равновесного выхода продуктов реакции от температуры и давления
Вывод
1 Рассматриваемая реакция протекает с поглощением тепла и является эндотермической, т.к. Н > 0.
2 Реакция термодинамически возможна в области температур начиная с 700 К до 1200К, т.к. в этой области температур энергия Гиббса G < 0.
3 Начиная с температуры выше 700 К равновесный выход продуктов реакции достигает достаточной для практических целей значений.
4 С увеличением давления в ходе реакции понижается равновесный выход продуктов реакции.