Билет № 8

1. Численной интегрирование.

Вычислить определенный интеграл методом трапеции с шагом h=2. Найти оценки погрешности.

2. Сетевые графики. Критический путь. Оптимизация графика по времени в зависимости от вложенных средств.

Задача

Дан сетевой график с указанием вероятностного времени выполнения работ, ­­ – минимальное время выполнения работы , ­ – коэффициент пропорциональности зависимости времени работ от вложенных средств в работу .

Оптимизировать сетевой график по времени (уменьшение времени выполнения проекта) за счет вложенных средств, если они не превышают 12 ден. единиц, построить модель для расчета оптимального плана.

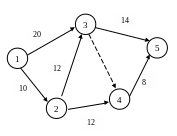
(1, 2) (2, 3) (1, 3) (2, 4) (3, 4) (3, 5) (4, 5)	6 8 12 7 0 10 6	0,01 0,05 0,02 0,03 0 0,04 0,02

Билет № 9

1. Численное интегрирование.

Вычислить интеграл методом Симпсона с шагом h=1. Найти оценки погрешности.

2. Сетевые графики. Вероятностные сети. Оценка времени выполнения работ.

Задача

Задан сетевой график с оценками времени выполнения работ.

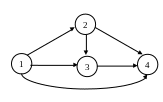
	Оптимистическая оценка	Пессимистическая оценка	Вероятностная оценка
(1, 2) (1, 3) (1, 4) (2, 4) (3, 4)	18 12 20 10 9	30 22 36 22 15

Определить дисперсию критического пути и вероятность выполнения проекта за 45 дней.

Билет № 10

1. Численное интегрирование.

Вычислить определенный интеграл методом трапеции с шагом h=2. Найти оценки погрешности.

2. Динамическое программирование. Распределение ресурса между предприятиями головной фирмой.

Задача

Фирме подчинены 3 предприятия. Головная фирма распределяет денежный ресурс в 100 тыс. ед. Прирост прибыли от получения ресурса на предприятиях задан таблично, дискретность распределения 20 тыс. ден. единиц. Составить план распределения из условия глобальной прибыли.

Средства	Прирост прибыли по предприятиям
	1	2	3
20 40 60 80 100	10 32 41 62 70	12 26 36 54 73	11 36 45 60 77

Билет № 11

1. Площадь поверхности тела вращения.

Задача

Найти площадь поверхности тела, образованного вращением вокруг оси дуги кривой , заключенной между точками , .

2. Задачи раскроя материалов и составления смеси. Области применений.

Задача

Строителям требуется комплекты досок, каждый комплект состоит из 3-х досок длиной 1,5 м и 8 досок длиной 0,6 м.

Как следует раскроить 680 четырехметровых досок, чтобы получить наибольшее количество комплектов? Составить модель и получить решение задачи симплекс-методом.

Варианты раскроя приведены в таблице.

Заготовки	Варианты раскроя
	1	2	3
	2 1	0 6	1 5