1)Преломление и отражение на сферической поверхности. Нулевой инвариант Аббе.

Предположим, что две среды с показателями преломления n1 и n2 разделяются сферической поверхностью Σ (рис. 3.2.). На ли­нии LL‘, проходящей через центр нашей сферы О, поместим точечный источник света L. Рассмотрим узкий гомо­центрический конус лучей, падающий из L на поверх­ность раздела двух сред.

Мы предполагаем пучок настолько узким, т.е. угол настолько малым, что практи­чески можно считать отрезок LS равным LA, L‘S равным L‘A и т.д. Такой узкий пучок будем называть параксиальным. Итак, условие параксиальности пучка есть

LS » LA и L‘S » L‘A.

Возьмем какой-либо луч из этого пучка, например LA, падающий на Σ под углом i, построим сопряженный ему преломленный луч AL‘ (угол преломления r) и найдем положение точки, в которой преломленный луч пересечет ось системы.

Из треугольника ALO имеем

из треугольника OAL’

Отсюда

В дальнейшем все отрезки вдоль оси будем отсчитывать от точки S, считая положительными отрезки, откладываемые от S вправо (в направлении распространяющегося света), и отрицательными — отрезки, откладываемые влево.Таким образом, AL » SL= — а1 , AL‘» SL‘= а2, AO = SO = R (радиус нашей сферы). В таком случае LO = -а1 + R, OL‘ = а2 — R. Используя закон преломления при переходе из первой среды во вторую, получим

• * =

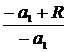т.е.

Последняя формула показывает, что произведение при преломлении сохраняет свою величину Q. Его называют нулевым инвариантом Аббе. Для многих целей этой формуле удобно придать вид

• =

2)Тонкая сферическая линза. Главная оптическая ось, главный фокус, оптический центр линзы, фокальная плоскость.

Виды линз.
		Линза может быть ограничена двумя выпуклыми сферическими поверхностями (двояковыпуклая линза - рис. а), выпуклой сферической поверхностью и плоскостью (плоско-выпуклая линза - рис. б), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза - рис. в). Эти линзы посередине толще, чем у краев, и все они называются выпуклыми: Линзы, которые посередине тоньше, чем у краев, называются вогнутыми. На рисунке изображены три вида вогнутых линз: двояковогнутая -а, плосковогнутая -б, выпукло-вогнутая -в:

Мы будем рассматривать наиболее простой случай, когда толщина линзы l=|AB| пренебрежимо мала по сравнению с радиусами R1 и R2 поверхностей линзы и расстоянием предмета от линзы.

Такую линзу называют тонкой линзой. В дальнейшем, говоря о линзе, будет подразумеваться именно тонкая линза. Точки А и B в тонкой линзе расположены столь близко друг к другу, что их можно принять за одну точку, которую называют оптическим центром линзы и обозначают точкой О. Луч света, проходящий через оптический центр линзы, практически не преломляется. Прямую О1О2, проходящую через центры сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью. Главная оптическая ось тонкой линзы проходит черезоптический центр. Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью.

Точка, в которой пересекаются после преломлений в собирающей линзе лучи, падающие на линзу параллельно главной оптической оси, называется главным фокусом линзы. Эту точку обозначают буквой F.

Фока́льная пло́скость в параксиальной оптике — плоскость, на которой расположены точки, в которых собираются попавшие в систему плоскопараллельные пучки лучей. В реальной оптике поверхность, обладающая такими свойствами, плоскостью, вообще говоря, не является. Аберрация, связанная с несоответствием данной поверхности с плоскостью, называется кривизной поля изображения.

Для тонких линз фокальной плоскостью является плоскость перпендикулярная главной оптической оси, проходящая через фокус.

3)Вывод формулы тонкой линзы. Оптическая сила линзы и Линейное увеличение

Из подобия треугольников, заштрихованных одинаково, следует

 откуда  

Разделив последнее равенство на произведение dfF,  получим:

, где d — расстояние предмета от линзы; f — расстояние от линзы до изображения, F — фокусное расстояние.

 - формула тонкой линзы

Оптическая сила линзы равна: 

Линейное увеличение

Из подобия заштрихован­ных треугольников следует: 

4)Собирающие и рассеивающие линзы. Ход лучей в собирающих и рассеивающих линзах для различия случаев расположения предмета относительно фокуса.

Линзы бывают собирающими и рассеивающими.

 

Собирающая линза в средней части толще и отклоняет лучи к оптической оси, если показатель преломления линзы больше показателя преломления среды.

 

Рассеивающая линза в средней части тоньше и отклоняет лучи от оптической оси.

 

Объясните такой ход лучей в линзах, применяя закон преломления.

Линза называется тонкой, если ее толщиной можно пренебречь. Схематически тонкая собирающая линза

изображается так:
а рассеивающая так:

Ход лучей в собирающей линзе

Как мы помним, собирающая линза называется так потому, что световой пучок, параллельный

главной оптической оси, после прохождения линзы собирается в её главном фокусе.

Пользуясь обратимостью световых лучей, приходим к следующему выводу: если в главном

фокусе собирающей линзы находится точечный источник света, то на выходе из линзы полу-

чится световой пучок, параллельный главной оптической оси.

Оказывается, что пучок параллельных лучей, падающих на собирающую линзу наклонно,

тоже соберётся в фокусе — но в побочном. Этот побочный фокус P отвечает тому лучу, который

проходит через оптический центр линзы и не преломляется.

Правила хода лучей в собирающей линзе:

1. Луч, идущий через оптический центр линзы, не преломляется.

2. Луч, идущий параллельно главной оптической оси линзы, после преломления пойдёт через главный фокус.

3. 3. Если луч падает на линзу наклонно, то для построения его дальнейшего хода мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Вот через этот побочный фокус и пойдёт преломлённый луч.

Ход лучей в рассеивающей линзе.

Наблюдая этот расходящийся пучок, мы увидим светящуюся точку, расположенную в фо-

кусе F позади линзы.

Если параллельный пучок падает на линзу наклонно, то после преломления он также станет

расходящимся. Продолжения лучей расходящегося пучка соберутся в побочном фокусе P, отве-

чающем тому лучу, который проходит через через оптический центр линзы и не преломляется.

Правила хода лучей в рассеивающей линзе:

1. Луч, идущий через оптический центр линзы, не преломляется.

2. Луч, идущий параллельно главной оптической оси линзы, после преломления начнёт удаляться от главной оптической оси; при этом продолжение преломлённого луча пройдёт через главный фокус.

3. Если луч падает на линзу наклонно, то мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Преломлённый луч пойдёт так, словно он исходит из этого побочного фокуса.

5)Сферическая и хроматическая аберрация и кома. Дисторсия.

Хроматическая аберрация

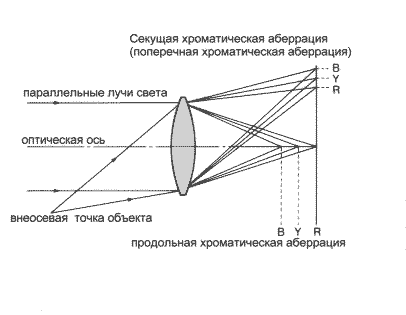
Когда белый свет (свет, состоящий из многих цветов, смешанных равномерно, в результате чего глаз не различает какого-то определенного цвета и, таким образом, воспринимает свет как белый), такой, как солнечный, проходит через призму, то можно наблюдать спектр радуги. Это явление имеет место, потому что показатель преломления призмы (и интенсивность дисперсии) бывает различной в зависимости от длинны волны (короткие волны преломляются более интенсивно, чем длинные). Хотя в призме оно видно самым наглядным образом, это явление также имеет место и в фотообъективах, и поскольку оно происходит при разных длинах волн, то оно называется хроматической аберрацией.  Есть два типа хроматической аберрации: "продольная хроматическая аберрация", при которой положение фокальной точки на оптической оси меняется в зависимости от длинны волны, и "хроматическая разница увеличения", при которой увеличение изображения в периферийных областях меняется в зависимости от длинны волны. На реальных фотографиях продольная хроматическая аберрация проявляется в виде размытости цвета или засветки, а хроматическая разница увеличения проявляется в виде цветовой окантовки (когда по границам краев виден цвет).  Хроматическая аберрация в фотообъективе корректируется путем сочетания различных типов оптического стекла, обладающих различными характеристиками преломления и дисперсии. Поскольку влияние хроматической аберрации возрастает при более значительных фокусных расстояниях, точная коррекция хроматической аберрации особенно важна в сверхтелефотообъективах, чтобы получить хорошую резкость изображения. Хотя существует предел степени коррекции, допускаемый оптическим стеклом, можно значительно улучшить результаты при помощи такого искусственного кристалла, как флюорит или стекло UD.  Хроматическую разницу увеличения можно назвать "поперечной хроматической аберрацией" (поскольку она происходит поперек оптической оси).  Примечание: в то время как хроматическая аберрация наиболее заметна при использовании цветной пленки, она влияет и на черно-белые изображения, проявляясь как уменьшение резкости.

Хроматическая аберрация

Сферическая аберрация   В определенной мере эта аберрация присутствует во всех объективах, построенных целиком из сферических элементов. Сферическая аберрация ведет к тому, что параллельные световые лучи, проходящие через край линзы, сливаются в фокальной точке ближе к линзе, чем световые лучи, проходящие через центр линзы. (Величина смещения фокальной точки вдоль оптической оси называется продольной сферической аберрацией.) Степень сферической аберрации имеет тенденцию увеличиваться в объективах с большой апертурой. Точечное изображение, подвергающееся влиянию сферической аберрации, с резкостью образует лучи света возле оптической оси, однако на него влияет засветка от периферических световых лучей (эта засветка также называется ореолом, а его радиус называют поперечной сферической аберрацией). В результате этого сферическая аберрация влияет на всю площадь изображения, от центра до его краев, и получается мягкое низко-контрастное изображение, которое кажется как будто покрытым тонкой вуалью.  Очень трудно исправить сферическую аберрацию в сферических объективах. Хотя это исправление обычно производится путем сочетания двух линз - одной выпуклой и одной вогнутой - на основе световых лучей с определенной высотой падения (расстоянием от оптической оси ), есть предел степени коррекции с использованием сферических линз, поэтому какая-то доля аберрации сохраняется всегда. Эту остаточную аберрацию можно в значительной степени ликвидировать путем диафрагмирования объектива, чтобы сократить поток периферийного света. При объективе с большой апертурой при полной апертуре единственный эффективный способ существенно компенсировать сферическую аберрацию состоит в том, чтобы использовать асферическую линзу. 

Сферическая аберрация

Кома (коматическая аберрация)   Кома или коматическая аберрация это явление, видимое на периферии изображения, которое создается объективом, скорректированным на сферическую аберрацию, и вызывает сведение световых лучей, поступающих на край объектива под каким-то углом, в форме кометы, а не в форме желаемой точки. Отсюда и ее название. Форма кометы ориентирована радиально, причем ее хвост направлен либо к центру, либо от центра изображения. Вызываемая этим размытость по краям изображения называется коматической засветкой. Кома, которая может иметь место даже в объективах, точно воспроизводящих точку как точку на оптической оси, вызывается разницей преломления между световыми лучами из точки, расположенной вне оптической оси, и проходящими через края объектива, и главным световым лучом от той же точки, проходящим через центр объектива. Кома увеличивается по мере увеличения угла главного луча и ведет к снижению контрастности по краям изображения. Определенной степени улучше ния можно добиться диафрагмированием объектива. Кома также может привести к засвечиванию размытых участков изображения, создавая неприятный эффект. Ликвидация как сферической аберрации, так и комы для объекта, расположенного на определенном съемочном расстоянии, называется апланатизмом, а объектив, скорректированный таким образом, называется апланатом.