Лабораторна робота №3 Вибір апроксимуючої функції за коефіцієнтом кореляції
Мета: обрати функцію за коефіцієнтом кореляції, яка найбільш точно описує стан обладнання.
Короткі теоретичні відомості
Коефіцієнтом
кореляції
для двох дискретних функцій називається
величина, яка показує ступінь тісноти
лінійного зв’язку цих функцій.
Визначається за формулою:
,
(3.1)
Якщо
коефіцієнт кореляції дорівнює нулю, то
значення двох вибірок не корельовано,
тобто вони лінійно не зв’язані. Проте
це не означає, що між ними не може бути
функціонального зв’язку. Так дві
випадкові величини x
та y,
рівномірно розподілені на колі, не
корельовані, проте пов’язані залежність
.
В даній роботі коефіцієнт кореляції допоможе нам знайти апроксимуючу функцію, яка найкраще описує набір опорних точок.
Порядок виконання роботи
Виконати апроксимації всіх семи функції із лабораторної роботи №2 (табл. 2) методом найменших квадратів для одного набору даних. Студент повинен взяти той набір даних, який відповідає його порядковому номеру.
Для одержаних апроксимуючих функцій розрахувати їх коефіцієнт кореляції з початковими даними. За найбільшим кореляційним коефіцієнтом обрати функцію, яка найбільш точно описує стан технічного обладнання. При цьому бажано, щоб вибір проводився автоматично за допомогою відповідної процедури.
Зробити висновки.
Приклад 3.1
Дано наступні експериментальні дані:
(x1; y1) |
(x2; y2) |
(x3; y3) |
(x4; y4) |
(x5; y5) |
(0,5; 6) |
(2; 5,1) |
(3,5; 3,8) |
(4,1; 2,4) |
(5,2; 0,5) |
Потрібно виконати апроксимацію всіх функцій із табл. 2 методом найменших квадратів. Потім визначити коефіцієнти кореляції для всіх функцій і обрати функцію з коефіцієнтом кореляції найближчим до 1.
В MathCad 2001і для апроксимації можна використовувати функцію genfit(x, y, g, G). Ця функція повертає вектор параметрів, що реалізують регресію даних за допомогою функції користувача загального вигляду (див. приклад 2.2).
Знайдемо частинні похідні. Наприклад для експоненціальної функції матимемо:
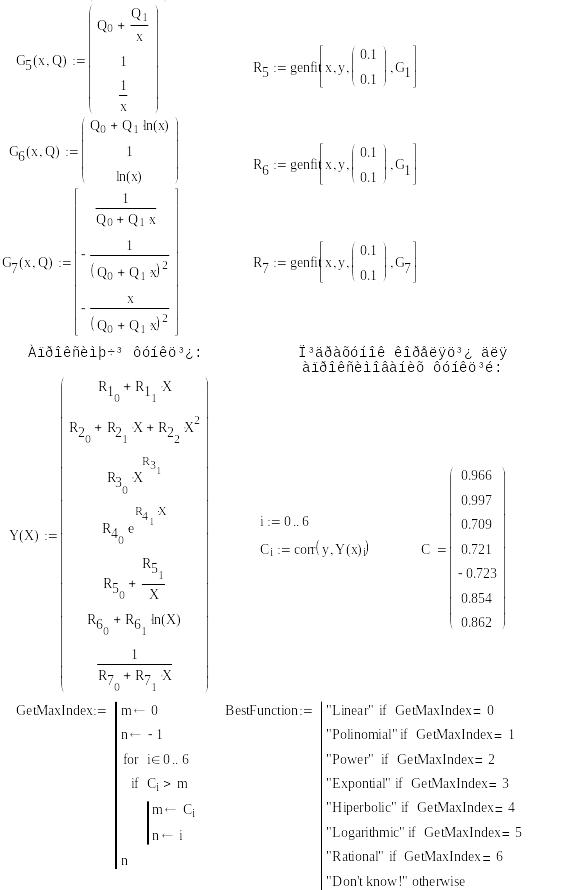
Звіт повинен містити
Тему та мету роботи.
Вихідні дані із табл. 2.
Апроксимацію функцій методом найменших квадратів для одного набору даних та їх коефіцієнт кореляції з початковими даними.
Графік апроксимуючої функції, що має найбільший коефіцієнт кореляції.
Висновки по результатам виконаної роботи.
Запитання для контролю
Що називається коефіцієнтом кореляції двох дискретних вибірок даних?
Чи може коефіцієнт кореляції мати від’ємне значення? Про що це свідчить?
Якщо відомо, що коефіцієнт кореляції близький до нуля, то чи можна стверджувати, що дані не мають ніякої функціональної залежності?
Що спільного між коефіцієнтом кореляції та кореляційною функцією?
Що таке центроване значення функції?
Як визначити математичне сподівання для випадкової вибірки даних?