2. Вычисление длины дуги кривой

Пусть кривая на плоскости задана уравнением у = f ( x ) или х =  ( у ). На кривой выбраны точки А и В с координатами: А(а; с), В(b; d). Длина l дуги от точки А до точки В вычисляется по формуле:

l = или l = .

Если кривая задана параметрическими уравнениями , t [t₁; t₂], то

длина дуги вычисляется по формуле l = .

Если кривая задана уравнениями в полярных координатах r = r ( φ ), α ≤ φ ≤ β,

то длина дуги кривой вычисляется по формуле l = .

Примеры.

30. Вычислить длину дуги кривой y = ln sin x от х = до х = π.

Предварительно вычислим : y = ln sin x, y′ = ,

= = , т.к. ≤ х ≤ π. Следовательно, l = = ln = ln – ln = 2ln .

31. Вычислить длину дуги астроиды x = a cos³t , y = a sin³t (см. рис. к задаче 27)

Найдем сначала ¼, т.е. длину дуги кривой, лежащей в I четверти:

= = =

= = = 3a =

= 3a = 3a = a. Следовательно, l = 6a.

32. Найти длину кардиоиды r = a (1 + cosφ).

Найдем сначала половину длины кривой: = =

= = a = a =

= a = –4a cos = –4a (0 – 1) = 4a. Значит, l = 8a.

3.3. Вычисление объемов тел

3.3.1. Вычисление объема тела по известным площадям поперечных сечений

Пусть в пространстве задано тело. Пусть построены

его сечения плоскостями, перпендикулярными оси Ох.

Площадь фигуры, образующейся в сечении, зависит от

точки х, определяющей плоскость сечения. Пусть эта

зависимость известна и задана непрерывной на [a, b]

функцией S (x). Тогда объем части тела, находя-

щейся между плоскостями х = а и х = b вычисляется

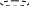
п о формуле

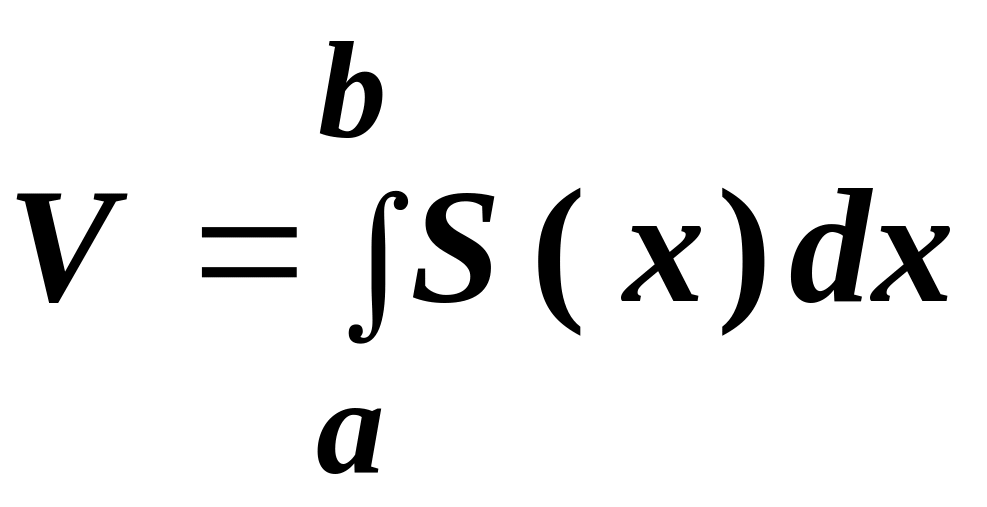
3.3.2. Объемы тела вращения,

образованного вращением вокруг оси

Ох ( или оси Оу) криволинейной трапеции,

ограниченной кривой y = f (x) (f (x) ≥ 0) и

прямыми y = 0, x = a, x = b, вычисляются

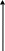
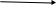
с оответственно по формулам: , .

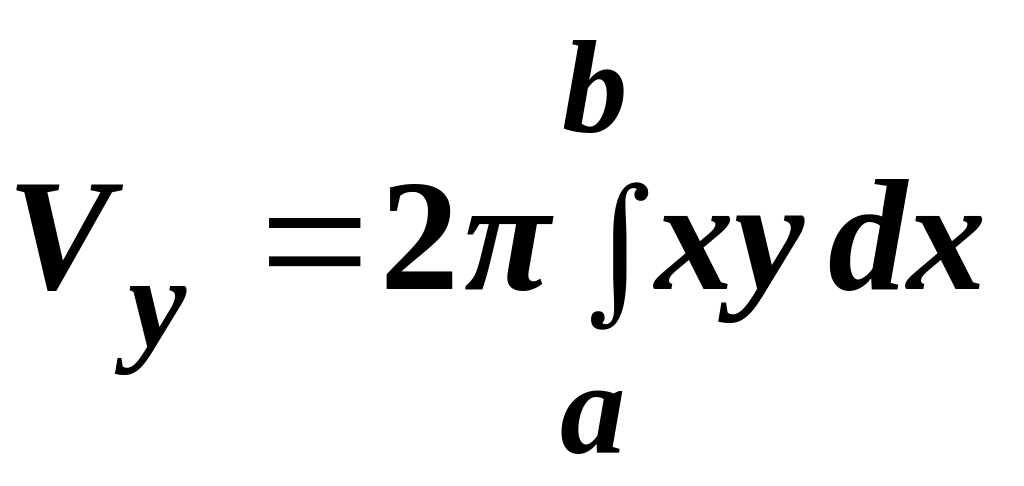Если тело образуется при вращении вокруг оси Оу криволинейной

трапеции, ограниченной кривой х = j (у) (j (у) ³ 0) и прямыми

х = 0, у = с, y = d, то объем тела вращения равен .

Примеры.

33. Н айти объем V пирамиды с площадью основания Q и высотой H.

Направим ось Ох перпендикулярно основанию пирамиды, а начало координат совместим

с вершиной О данной пирамиды. На расстоянии х от точки О проведем поперечное сечение

пирамиды. Его площадь обозначим через S, она является функцией от х: S = S (х).

Площади поперечного сечения (параллельного основанию) и основания относятся как

квадраты их расстояний от вершины, т.е. . Отсюда S (х) = х².

Следовательно, V = Q ∙H.

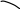
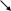
34. Найти объем тела, ограниченного поверхностями x² + 4y² = 1, z = x (x  0), z = 0.

В результате пересечения эллиптического цилиндра x² + 4y² = 1 плоскостями z = x и

z = 0 получим тело, изображенное на рисунке. Сечение тела, перпендикулярное оси Ох,

проведенное на расстоянии х от начала координат представляет собой прямоугольник ABCD.

Найдем его площадь S = S (х). Высота (ширина) MN прямоугольника равна х, т.е. | MN | = х

(в прямоугольном треугольнике NMO угол  NOM равен 45) . Точка D (x; y) лежит на эллипсе

x² + 4y² = 1. Значит, MD = y = , т.е. | MD | = => S(x) = AD ∙ MN =

2 MD ∙ MN = 2 ∙ ∙ x = x ∙ .

Следовательно, V = = – =

35. Найти объем тела, ограниченного двумя цилиндрами x² + y² = R² и x² + z² = R².

Изобразим на рисунке восьмую часть тела, расположенную в I октанте. В поперечном

сечении (перпендикулярном оси Ох) тела получится квадрат. Его сторона а равна ординате

т очки М (х; у), лежащей на окружности x² + y² = R² , т.е. S(x)= = R² – x².

С ледовательно,

36. Найти объем тела, образованного вращением фигуры, ограниченной линиями ху = 6, х = 1, х = 4, у = 0, вокруг оси Ох и вокруг оси Оу.

37. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями y = e^–x, x = 0,

y = 0 (x  0). y = e^–x => x = –ln y => V_y = π = π = =

= = = = –2π (0 – 1) = 2π.

38. Найти объем тела, образованного вращением вокруг оси Оx арки циклоиды , 0 ≤ t ≤ 2π.

V_x = π = π = πa³ =

= πa³ = πa³ =

= πa³ = πa³ =

= πa³ πa³∙ 5 π = 5π²a³.

39. Найти объем тела, образованного вращением вокруг прямой х = – 2 области, ограниченной линиями

у = x³ , х = –1, х = 0, y = 4 .

Перенесем начало координат в точку О₁(–2; 1), сохранив направления осей (рис.) . В новой

с истеме координат уравнение кубической параболы примет вид у = (х₁ – 2)³ => х₁ = 2 + .

Объем V_н нижней части тела (под осью Ох) найдем как разность двух объемов V_н = V₁ – V₂ ,

где V₂ = π = π , V₁ = π = π (или как объем цилиндра с высотой 1 и

радиусом основания 1). Имеем: V_н = π – π = π. Объем V_в верхней части тела (над

осью Ох), очевидно, равен V_в = 12π (как разность объемов круговых цилиндров:

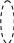
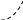
V = π ∙ 4 ∙ 4 – π ∙ 1 ∙ 4 = 12π ). Т.о. V = V_н + V_в = π + 12 π = π.

40. Найти объем тела, образованного вращением вокруг оси Ох фигуры,

ограниченной графиками функций у = 2х – х², у = –х + 2.

Графики функций (см. рис.) пересекаются в точках (1; 1) и (2; 0) =>

=> V = – = =

= = = .