
Лабораторные работы по физике твёрдого тела
Лабораторная работа №3
ТУННЕЛЬНЫЙ ЭФФЕКТ В ВЫРОЖДЕННОМ
P-N ПЕРЕХОДЕ
ЦЕЛЬ РАБОТЫ
Цель работы заключается в изучении туннельного эффекта и ис-следовании особенностей проявления туннельного эффекта в тун-нельном диоде.
ТУННЕЛЬНЫЙ ЭФФЕКТ
Туннельный эффект на прямоугольном потенциальном барьере
Пусть
в некоторой области пространства имеется
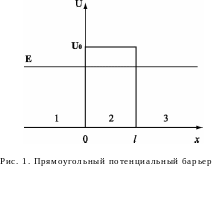
потенциаль-ный барьер конечной высоты
![]() ширины
ширины
![]() (см.
рис.1). Тогда по классическим представлениям
частица с кинетической энергией
(см.
рис.1). Тогда по классическим представлениям
частица с кинетической энергией
![]() всегда
преодолевает барьер, а частица с энергией,
меньшей
всегда
преодолевает барьер, а частица с энергией,
меньшей
![]() него зеркально отражается.
него зеркально отражается.
В
действительности существует отличная
от нуля вероятность проникновения
частиц с энергией
![]() через
потенциальный барьер. Явление прохождения
частицы через потенциальный барь-ер в
тех случаях, когда кинетическая энергия
частицы меньше вы-соты потенциального
барьера, называется туннельным эффектом
(туннелированием).
через
потенциальный барьер. Явление прохождения
частицы через потенциальный барь-ер в
тех случаях, когда кинетическая энергия
частицы меньше вы-соты потенциального
барьера, называется туннельным эффектом
(туннелированием).
Кажущаяся
парадоксальность этого явления состоит
в том, что при нахождении частицы внутри
потенциального барьера (в облас-ти
пространства
![]() )
частица
обладает потенциальной энер-гией
большей,
чем её первоначальная энергия
)
частица
обладает потенциальной энер-гией
большей,
чем её первоначальная энергия
![]() ,
т.е. проис-ходит как бы нарушение закона
сохранения энергии. Отмеченный парадокс
объясняется в квантовой механике на
основе соотноше-ния неопределённостей
для энергии и времени.
,
т.е. проис-ходит как бы нарушение закона
сохранения энергии. Отмеченный парадокс
объясняется в квантовой механике на
основе соотноше-ния неопределённостей
для энергии и времени.
Можно отметить и другой эффект, наблюдаемый при падении частицы на потенциальный барьер: имеется отличная от нуля ве-роятность отражения от барьера и в том случае, когда энергия час-тицы больше высоты потенциального барьера. Оба эти явления считаются сугубо квантово–механическими эффектами и не имеют аналогов в классической механике.
Для вычисления вероятности прохождения микрочастицы через потенциальный барьер необходимо решить уравнение Шредингера:
![]() (1)
(1)
с потенциальной энергией заданного вида (см. рис.1).
В различных областях пространства (области 1, 2, 3 на рис.1) уравнению Шредингера (1) удовлетворяют следующие волновые функции:
![]()
![]() ,
(2)
,
(2)
![]() ,
,
где
![]()
![]() ,
,
![]() – мнимая
единица
– мнимая
единица
![]() .
.
Первое
слагаемое в функции
![]() описывает
волну, падающую на потенциальный барьер,
а функция
описывает
волну, падающую на потенциальный барьер,
а функция
![]() описывает
волну, связанную с движением микрочастицы,
прошедшей через барьер и продолжа-ющей
движение в положительном направлении
оси
описывает
волну, связанную с движением микрочастицы,
прошедшей через барьер и продолжа-ющей
движение в положительном направлении
оси
![]() .
Если при-нять амплитуду падающей волны
.
Если при-нять амплитуду падающей волны
![]() ,
то квадрат модуля ампли-туды
,
то квадрат модуля ампли-туды
![]() определяет
вероятность прохождения частицы через
по-тенциальный барьер:
определяет
вероятность прохождения частицы через
по-тенциальный барьер:
![]() .
(3)
.
(3)
В
частном случае, когда
![]() ,
т.е. коэффициент прохождения мал:
,
т.е. коэффициент прохождения мал:
![]() ,
(4)
,
(4)
где
![]() .
.
Из
формулы (4) видно, что вероятность
туннелирования сильно зависит (по
экспоненциальному закону) от ширины
потенциаль-ного барьера и при малой
ширине барьера
может
достигать зна-чительной величины. Так,
например, именно туннельным эффек-том
объясняется преодоление потенциального
барьера при перехо-де электрона от
одного иона к другому при его движении
по крис-таллу. Другие проявления
туннельного эффекта: радиоактивный
![]() –
распад ядер, автоэлектронная эмиссия,
эффект Джозефсона в сверхпроводниках.
–
распад ядер, автоэлектронная эмиссия,
эффект Джозефсона в сверхпроводниках.
Туннельный диод (тд)
Туннельный эффект составляет физическую основу действия об-щего класса полупроводниковых приборов – туннельных диодов.
Принцип действия ТД можно пояснить на основе представлений о зонной энергетической структуре твёрдых тел. В процессе обра-зования твёрдых тел электронные энергетические уровни отдель-ных атомов из-за взаимодействия электронов смещаются и обра-зуют энергетические полосы – разрешённые зоны. Разрешённые зо-ны чередуются с зонами энергий, которых электроны принимать не могут. Такие зоны называются запрещёнными.
В полупроводниках самая верхняя зона
разрешённых энергий называется зоной
проводимости. Соседняя зона разрешённых
энер-гий с меньшими значениями энергии
электронов называется валентной зоной.
Обе эти зоны образованы энергетическими
уров-нями валентных электронов в
свободных атомах. Валентная зона и зона
проводимости разделены интервалом
значений энергий, кото-рые электрон
иметь не может – зоны запрещённых
энергий с энер-гетической шириной
полупроводниках самая верхняя зона
разрешённых энергий называется зоной
проводимости. Соседняя зона разрешённых
энер-гий с меньшими значениями энергии
электронов называется валентной зоной.
Обе эти зоны образованы энергетическими
уров-нями валентных электронов в
свободных атомах. Валентная зона и зона
проводимости разделены интервалом
значений энергий, кото-рые электрон
иметь не может – зоны запрещённых
энергий с энер-гетической шириной
![]() (см.рис.2). В примесных полупроводниках
атомы примесей образуют свои локальные
уровни энергий, рас-положенные внутри
запрещённой зоны. При температуре,
отличной от абсолютного нуля, часть
электронов с примесных уровней,
рас-положенных вблизи «дна» зоны
про-водимости, переходит в зону
проводимости. Примеси, поставляющие
электроны в зону про-водимости, называются
донорными примесями, а полупроводники,
в которых основные носители тока
электроны – электронными по-лупроводниками
или полупроводниками
(см.рис.2). В примесных полупроводниках
атомы примесей образуют свои локальные
уровни энергий, рас-положенные внутри
запрещённой зоны. При температуре,
отличной от абсолютного нуля, часть
электронов с примесных уровней,
рас-положенных вблизи «дна» зоны
про-водимости, переходит в зону
проводимости. Примеси, поставляющие
электроны в зону про-водимости, называются
донорными примесями, а полупроводники,
в которых основные носители тока
электроны – электронными по-лупроводниками
или полупроводниками
![]() –типа.
–типа.
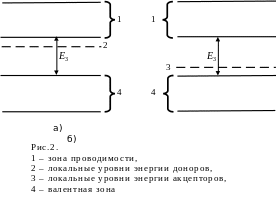
Если
при введении примесей локальные уровни
электронов об-разуются вблизи вершины
валентной зоны и в нормальном сос-тоянии,
т.е. при
![]() не заполнены, то при повышении темпе-ратуры
электроны из валентной зоны могут
перейти на эти ло-кальные примесные
уровни. При этом в валентной зоне
образуются вакантные для электронов
места – дырки, которые могут свободно
перемещаться по кристаллу, обладая
свойствами носителей заряда с положительным
знаком. Примеси, поставляющие дырки в
валент-ную зону, называются акцепторными
примесями, а полупровод-ники, в которых
основные носители тока – дырки, называются
ды-рочными полупроводниками или
полупроводниками
не заполнены, то при повышении темпе-ратуры
электроны из валентной зоны могут
перейти на эти ло-кальные примесные
уровни. При этом в валентной зоне
образуются вакантные для электронов
места – дырки, которые могут свободно
перемещаться по кристаллу, обладая
свойствами носителей заряда с положительным
знаком. Примеси, поставляющие дырки в
валент-ную зону, называются акцепторными
примесями, а полупровод-ники, в которых
основные носители тока – дырки, называются
ды-рочными полупроводниками или
полупроводниками
![]() –
типа.
–
типа.
Количество электронов в зоне проводимости и дырок в валент-ной зоне определяется типом примесей и их концентрацией. С по-мощью методов статистической физики получены формулы, поз-воляющие по известной концентрации примесей и их энергии акти-вации рассчитать концентрацию свободных носителей тока в зонах и их распределение по энергетическим состояниям. Для этой цели вводятся понятия: уровень Ферми, плотность электрических сос-тояний, функция распределения электронов по энергиям.
Плотность
энергетических состояний
![]() определяется
по фор-муле:
определяется
по фор-муле:
![]() ,
(5)
,
(5)
где
![]() –
количество квантовых состояний в данном
образце материала объёмом
–
количество квантовых состояний в данном
образце материала объёмом
![]() в интервале значений энергии
в интервале значений энергии
![]() .
.
Функция
распределения электронов по энергиям
![]() определяется
по формуле:
определяется
по формуле:
![]() (6)
(6)
где
![]() – количество электронов в интервале
значений энергий
– количество электронов в интервале
значений энергий
![]() ,
,
![]() –
количество свободных электронов в
данном образце.
–
количество свободных электронов в
данном образце.
Далее
будут приведены точные выражения для
функции
![]() и
.
Однако для понимания принципа действия
туннельного диода достаточно знать,
что электроны в зоне проводимости
полупровод-ника распределены по
электрическим уровням неравномерно.
Функ-ция распределения
при некоторой энергии
и
.
Однако для понимания принципа действия
туннельного диода достаточно знать,
что электроны в зоне проводимости
полупровод-ника распределены по
электрическим уровням неравномерно.
Функ-ция распределения
при некоторой энергии
![]() имеет максимум, т.е. большинство электронов
обладает энергией вблизи этого зна-чения
,
причём само значение
расположено несколько выше «дна» зоны
проводимости. Следовательно, максимум
функции распре-деления дырок по энергиям
расположен несколько ниже вершины
ва-лентной зоны. Графики функции
для
электронов в зоне прово-димости и дырок
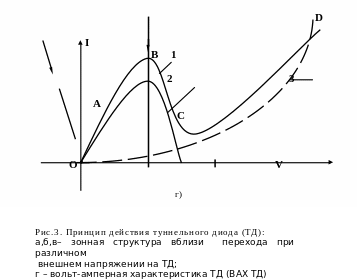
в валентной зоне приведены на рис.3.
имеет максимум, т.е. большинство электронов
обладает энергией вблизи этого зна-чения
,
причём само значение
расположено несколько выше «дна» зоны
проводимости. Следовательно, максимум
функции распре-деления дырок по энергиям
расположен несколько ниже вершины
ва-лентной зоны. Графики функции
для
электронов в зоне прово-димости и дырок
в валентной зоне приведены на рис.3.
При
контакте двух полупроводников с разным
типом проводи-мости на границе контакта
возникает узкая область с уникальными
физическими свойствами. Эта область
называется
![]() переходом.
переходом.
Свойства перехода используются для создания разных типов полупроводниковых приборов.
В
обычных полупроводниковых диодах
концентрация примеси не превышает, как
правило,
![]() атомов/м3,
и толщина области
пе-рехода в них составляет величину
порядка
атомов/м3,
и толщина области
пе-рехода в них составляет величину
порядка
![]() .
ТД изготовляют из сильнолегированных
полупроводников, называемых вырожден-ными
полупроводниками. В них концентрация
примесей составляет около
.
ТД изготовляют из сильнолегированных
полупроводников, называемых вырожден-ными
полупроводниками. В них концентрация
примесей составляет около
![]() атомов/м3,
а толщина
перехода около
атомов/м3,
а толщина
перехода около
![]() ,
то есть равна толщине
,
то есть равна толщине
![]() атомных плоскостей. В этих условиях
возмо-жен туннельный переход свободных
носителей тока из полупро-водника одного
типа в другой. Сильное легирование
полупроводников приводит к заметному
изменению вольт–амперной характеристики
перехода, когда обе области и
атомных плоскостей. В этих условиях
возмо-жен туннельный переход свободных
носителей тока из полупро-водника одного
типа в другой. Сильное легирование
полупроводников приводит к заметному
изменению вольт–амперной характеристики
перехода, когда обе области и
![]() -типа
и
-типа
и
![]() -типа
сильно ле-гированы. Этот эффект впервые
был обнаружен Есаки. Вольт–ампер-ная
характеристика диода Есаки показана
на рис.3г (кривая 1).
-типа
сильно ле-гированы. Этот эффект впервые
был обнаружен Есаки. Вольт–ампер-ная
характеристика диода Есаки показана
на рис.3г (кривая 1).
Рассмотрим зонную структуру полупроводника в области пе-рехода и в непосредственной близости от него при различном внеш-нем напряжении на ТД. На рис.3а изображена зонная структура при отсутствии напряжения на диоде. Вдоль вертикальной оси отложена энергия носителей тока.
При
образовании контакта дырки из
–области
переходят в
–об-ласть,
рекомбинируя там с электронами. При
этом в
–области
кон-такта после ухода положительно
заряженных дырок остаётся неском-пенсированный
отрицательный заряд, образованный
отрицательно за-ряженными ионами
акцепторов. Аналогично этому в
–области
воз-никает пространственный положительный
заряд, образованный поло-жительно
заряженными ионами доноров. Таким
образом, в
пере-ходе возникает электрическое поле,
напряженность которого направ-лена от
–области
к
–области,
и это поле препятствует дальнейше-му
переходу дырок в
–область
и электронов в
–область.
Теперь, чтобы, например, дырке перейти
из
–области
в
-область,
надо преодолеть это поле и определяемый
им потенциальный барьер, равный
![]() ,
где
,
где
![]() –
контактная разность потенциалов
пере-хода.
–
контактная разность потенциалов
пере-хода.
Несмотря
на наличие потенциального барьера, всё
же находятся электроны и дырки, энергия
которых достаточна для преодоления
этого барьера, поэтому через
переход текут токи электронов
![]() и
дырок
и
дырок
![]() (см. рис. 3), создавая в сумме диффузионный
ток
перехода.
Конечно, при отсутствии внешнего
напряжения диф-фузионный ток компенсируется
обратным током неосновных носи-телей
(не показан на рисунке), так что полный
ток через
пере-ход равен нулю.
(см. рис. 3), создавая в сумме диффузионный
ток
перехода.
Конечно, при отсутствии внешнего
напряжения диф-фузионный ток компенсируется
обратным током неосновных носи-телей
(не показан на рисунке), так что полный
ток через
пере-ход равен нулю.
При подаче на переход внешнего напряжения в прямом на-правлении (полюс «плюс» батареи присоединен к –области, по-люс «минус» – к –области) величина потенциального барьера для основных носителей тока уменьшается, что приведёт к увеличению диффузионного тока через переход. Так образуется прямая ветвь вольт-амперной характеристики (ВАХ) обычных диодов: при монотонном увеличении напряжения на диоде монотонно увели-чивается ток через диод, что изображено пунктирной прямой 3 на рис.3г.
Однако в ТД, кроме диффузионного тока, существует идущий в том же направлении туннельный ток. Характерной особенностью туннельного эффекта является то, что частица, пройдя через потен-циальный барьер, обладает той же энергией, что и до туннелирова-ния. В равновесных условиях большинство занятых электронных состояний (то есть состояний свободных от дырок) в области –типа лежит против занятых электронных состояний в области –типа. Следовательно, между ними возможно очень небольшое число обме-нов электронами (рис.4,О). Однако, как только будет приложено на-пряжение, некоторые занятые электронные состояния в –области окажутся напротив пустых электронных состояний (занятых дыроч-ных) в –области. Это приведет к плавному росту прямого тока (рис.4,А). Такое увеличение будет продолжаться до тех пор, пока энергетические состояния, заполненные дырками в –области не пе-рекроются полностью состояниями, заполненными электронами в –области (рис.4,B). Дальнейшее увеличение напряжения приведет к уменьшению этого перекрытия. Ток достигает максимума, а затем быстро падает. Поэтому туннельный ток будет максимальным в том случае, если у электронов, переходящих из –области в –область, будут свободны электронные состояния с той же энергией.
Другими словами, туннельный ток будет максимальным, если максимумы функции распределения по энергиям электронов и ды-рок будут приходиться на одни и те же значения энергии.
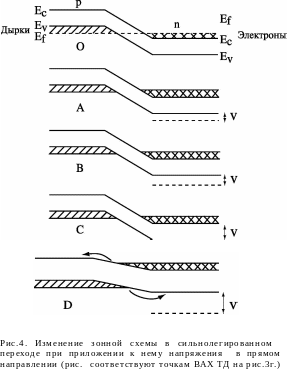
На
рис.3а–3в изображены графики функций
распределения электронов
![]() в зоне проводимости и дырок
в зоне проводимости и дырок
![]() в валентной зоне, а также относительное
смещение энергетических зон в зави-симости
от внешнего напряжения на диоде. Максимумы
функции распределения находятся вблизи
уровня Ферми, но несколько сме-щены от
него, поэтому при отсутствии внешнего
напряжения (рис.3а) для электронов в
–области
почти нет свободных энер-гетических
состояний с той же энергией в
–области,
поэтому туннелирование невозможно. При
увеличении внешнего напря-жения в прямом
направлении величина потенциального
барьера уменьшается, максимумы функций
распределения электронов и ды-рок
смещаются навстречу друг другу, и
туннельный ток увели-чивается. Наконец,
при некотором внешнем напряжении
макси-мумы распределения электронов и
дырок будут приходиться на одинаковые
значения энергии, и туннельный ток при
этом будет максимальным. Эта ситуация
изображена на рис.3б, где для на-глядности
изображены в виде кружочков электроны
и дырки с энергией, соответствующей
максимуму функции распределения, и
туннельный ток между ними.
в валентной зоне, а также относительное
смещение энергетических зон в зави-симости
от внешнего напряжения на диоде. Максимумы
функции распределения находятся вблизи
уровня Ферми, но несколько сме-щены от
него, поэтому при отсутствии внешнего
напряжения (рис.3а) для электронов в
–области
почти нет свободных энер-гетических
состояний с той же энергией в
–области,
поэтому туннелирование невозможно. При
увеличении внешнего напря-жения в прямом
направлении величина потенциального
барьера уменьшается, максимумы функций
распределения электронов и ды-рок
смещаются навстречу друг другу, и
туннельный ток увели-чивается. Наконец,
при некотором внешнем напряжении
макси-мумы распределения электронов и
дырок будут приходиться на одинаковые
значения энергии, и туннельный ток при
этом будет максимальным. Эта ситуация
изображена на рис.3б, где для на-глядности
изображены в виде кружочков электроны
и дырки с энергией, соответствующей
максимуму функции распределения, и
туннельный ток между ними.
При дальнейшем увеличении напряжения максимумы распре-делений вновь смещаются друг относительно друга и туннельный ток уменьшается. Зависимость туннельного тока от внешнего на-пряжения изображена пунктирной кривой 2 на рис.3г.
Суммарный ток через ТД в прямом направлении состоит из сум-мы туннельного тока и диффузионного тока. Его зависимость от внешнего напряжения, представляющая собой ВАХ ТД в прямом направлении, изображена на рис.3г (кривая 1). Из рисунка видна физическая природа явления возникновения ниспадающей ветви как следствие резкого увеличения, а затем столь же быстрого уменьшения туннельного тока.
В
области ниспадающей ветви ВАХ динамическое
сопротив-ление
![]() диода
диода
![]() является отрицательной величиной.
Эле-мент с отрицательным сопротивлением
позволяет создавать раз-личные
радиоэлектронные устройства: усилители,
генераторы, пе-реключатели.
является отрицательной величиной.
Эле-мент с отрицательным сопротивлением
позволяет создавать раз-личные
радиоэлектронные устройства: усилители,
генераторы, пе-реключатели.
Снятие
ВАХ ТД отличается рядом особенностей,
обусловленных отрицательным динамическим
сопротивлением диода на падающем участке
характеристики от
![]() до
до
![]() (см.рис.3).
Если нагру-зочное сопротивление диода,
т.е. общее сопротивление цепи, под-ключённой
к диоду, включая сопротивление источника
питания и измерительных приборов, больше
динамического отрицательного сопротивления
диода, то измерить ниспадающую ветвь
ВАХ не-возможно. Вместо статической ВАХ
наблюдается кривая гистере-зисного
типа (точки 1–4 и штриховые прямые на
рис.5в).
(см.рис.3).
Если нагру-зочное сопротивление диода,
т.е. общее сопротивление цепи, под-ключённой
к диоду, включая сопротивление источника
питания и измерительных приборов, больше
динамического отрицательного сопротивления
диода, то измерить ниспадающую ветвь
ВАХ не-возможно. Вместо статической ВАХ
наблюдается кривая гистере-зисного
типа (точки 1–4 и штриховые прямые на
рис.5в).
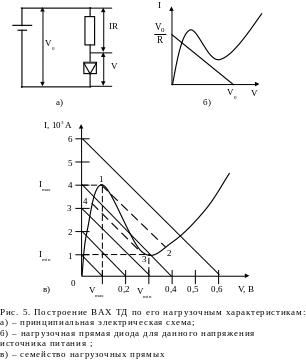
Для
понимания особенности изменения ВАХ
ТД рассмотрим схему из последовательно
соединённых ТД и резистора
![]() ,
пока-занную на рис.5а. Для того, чтобы
найти ток через диод, нанесём нагрузочную
прямую на ВАХ диода, как показано на
рис.5б.
,
пока-занную на рис.5а. Для того, чтобы
найти ток через диод, нанесём нагрузочную
прямую на ВАХ диода, как показано на
рис.5б.
![]()
 .
(7)
.
(7)
Точка
пересечения нагрузочной прямой (7) и ВАХ
показывают ток и напряжение на диоде
при данном внешнем напряжении
.
Если плавно увеличивать внешнее
напряжение
![]() ,
то получим се-мейство нагрузочных
прямых, изображённых на рис.5в.
,
то получим се-мейство нагрузочных
прямых, изображённых на рис.5в.
Заметим,
что при увеличении
от
нуля до
![]() нагрузочная прямая пересекает
характеристику в одной точке, и ток
постоянно возрастает.
нагрузочная прямая пересекает
характеристику в одной точке, и ток
постоянно возрастает.
В
окрестности
![]() нагрузочная прямая пересекает
характеристику в трёх точках. При этом
два решения, отвечающие внешним точкам
пересечения, устойчивы, а решение,
отвечающее внутренней точке, неустойчиво.
При приближении
к
нагрузочная прямая пересекает
характеристику в трёх точках. При этом
два решения, отвечающие внешним точкам
пересечения, устойчивы, а решение,
отвечающее внутренней точке, неустойчиво.
При приближении
к
![]() нагрузочная кривая схо-дит с горба
характеристики, и мы опять получаем
одно решение. Таким образом, при плавном
увеличении напряжения после про-хождения
точки 1 ВАХ (рис.5в) будет наблюдаться
скачок тока и скачкообразный переход
к точке 2 ВАХ. При плавном уменьшении
напряжения аналогичный скачок произойдёт
в точке 3 ВАХ, и из-мерить полностью ВАХ
ТД при данном нагрузочном сопротив-лении
оказывается невозможным. Для измерения
ВАХ ТД на нис-падающей ветви надо
уменьшить нагрузочное сопротивление
диода до такой величины, чтобы оно было
меньше (по модулю) дина-мического
отрицательного сопротивления ТД.
нагрузочная кривая схо-дит с горба
характеристики, и мы опять получаем
одно решение. Таким образом, при плавном
увеличении напряжения после про-хождения
точки 1 ВАХ (рис.5в) будет наблюдаться
скачок тока и скачкообразный переход
к точке 2 ВАХ. При плавном уменьшении
напряжения аналогичный скачок произойдёт
в точке 3 ВАХ, и из-мерить полностью ВАХ
ТД при данном нагрузочном сопротив-лении
оказывается невозможным. Для измерения
ВАХ ТД на нис-падающей ветви надо
уменьшить нагрузочное сопротивление
диода до такой величины, чтобы оно было
меньше (по модулю) дина-мического
отрицательного сопротивления ТД.
