Степень вершины графа

311. Задание {{ 311 }} ТЗ № 311

Отметьте правильный ответ

Вершина является изолированной, если:









312. Задание {{ 312 }} ТЗ № 312

Отметьте правильный ответ

Вершина является висячей, если:









313. Задание {{ 313 }} ТЗ № 313

Отметьте правильный ответ

Степень изолированной вершины равна:

 1

 0

 2

 3

314. Задание {{ 314 }} ТЗ № 314

Отметьте правильный ответ

Степень висячей вершины равна:

 1

 0

 2

 3

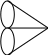
315. Задание {{ 315 }} ТЗ № 315

Отметьте правильный ответ

Наибольшая из степеней вершин графа

равна:

 3

 4

 5

 14

316. Задание {{ 316 }} ТЗ № 316

Отметьте правильный ответ

Наименьшая из степеней вершин графа

.

равна:

 1

 0

 3

 4

317. Задание {{ 317 }} ТЗ № 317

Отметьте правильный ответ

Наибольшая из степеней вершин графа

.

равна:

 3

 1

 5

 4

318. Задание {{ 318 }} ТЗ № 318

Отметьте правильный ответ

В графе кенигсбергских мостов наименьшая из степеней его вершин равна:

 2

 3

 5

 6

319. Задание {{ 319 }} ТЗ № 319

Отметьте правильный ответ

Если вершина графа не является ни изолированной и ни висячей, то ее степень удовлетворяет условию









320. Задание {{ 320 }} ТЗ № 320

Отметьте правильный ответ

Если вершина является граничной для кратных ребер и петли, то ее степень удовлетворяет условию:









Теорема о степенях вершин неориентированного графа

321. Задание {{ 321 }} ТЗ № 321

Отметьте правильный ответ

Сумма степеней вершин графа

равна:

 13

 12

 11

 10

322. Задание {{ 322 }} ТЗ № 322

Отметьте правильный ответ

Сумма степеней вершин неориентированного графа с ребрами удовлетворяет условию:









323. Задание {{ 323 }} ТЗ № 323

Отметьте правильный ответ

Сумма степеней вершин простого графа с неизолированными вершинами:







