Введение

Задачей большинства физико-химических экспериментов является количественное изучение каких-либо свойств вещества. Для этого проводятся измерения одной или нескольких физических величин с последующей обработкой полученных данных. Экспериментальные результаты всегда содержат погрешности, связанные с тем, что любые измерения сопровождаются действием и взаимодействием большого числа разнообразных и трудноучитываемых факторов. Конечной целью любого исследования является не только представление наилучшей, по мнению экспериментатора, оценки измеряемой величины, но и максимально достоверной оценки погрешности измерений.

Любой прибор или устройство для измерения физических величин можно рассматривать в виде объекта (рис. 1), для которого x₁, …, x_k — входные измеряемые и регулируемые параметры; w₁, …, w_l — неконтролируемые, случайным образом изменяющиеся параметры («шум» объекта); y₁, …, y_m — выходные параметры. Комплекс параметров x₁, …, x_k называют основным, поскольку он определяет условия эксперимента. Результат опыта зависит не только от основных параметров, но и от «шума» объекта, влияние которого носит случайный характер. Поэтому естественно рассматривать и результат эксперимента, и ошибку измерения как случайные величины, управляемые вероятностными законами, и применять для учета действия случайных факторов теорию вероятностей. Тогда влияние случайных ошибок на результат измерения можно количественно оценить при помощи математической статистики — науки, занимающейся применением вероятностных методов к решению задач в различных областях наук, в частности в задаче обработки результатов наблюдений.

Современная химическая промышленность выпускает несколько десятков тысяч наименований продуктов, в лабораториях разрабатываются сотни новых технологических процессов. Экспериментальное изучение механизмов протекания всех этих процессов нереально, между тем задачи оптимизации и управления этими процессами необходимо решать. Для этих целей успешно применяются экспериментально-статистические методы, с помощью которых составляется математическая модель объекта и при неизвестном механизме протекающих в объекте процессов изучается зависимость отклика системы на изменения основных параметров.

Р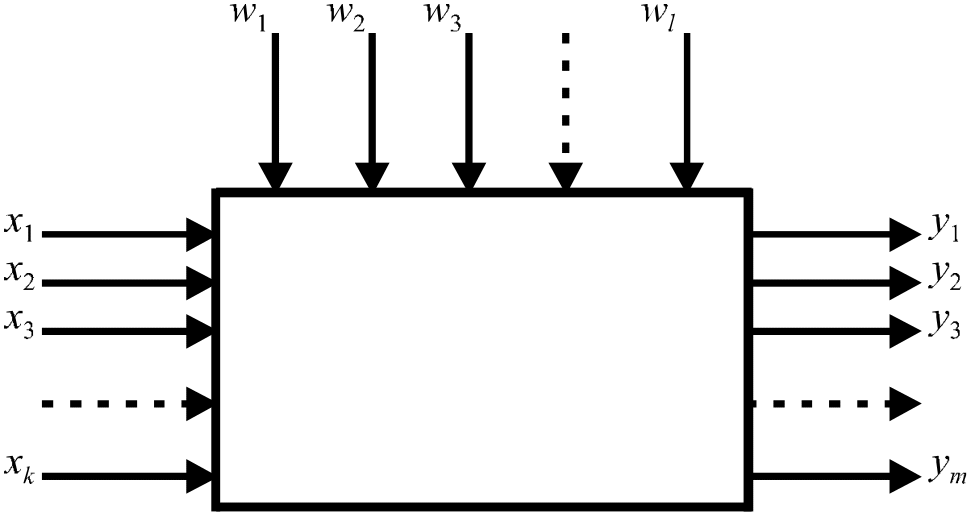 ис. 1. Схема объекта.

Математической моделью объекта служит функция отклика, связывающая выходной параметр, характеризующий результаты эксперимента, с переменными, которые варьируют при проведении опытов:

y =  (x₁, x₂,…, x_k).

Независимые переменные x₁, x₂,…, x_k называют факторами, пространство с координатами x₁, x₂,…, x_k — факторным пространством, а геометрическое изображение функции отклика в факторном пространстве — поверхностью отклика.

Эффективность экспериментов в большой степени зависит от методов их проведения. Пассивный эксперимент является традиционным методом, когда ставится большая серия опытов с поочередным варьированием каждой из переменных. Обработка опытных данных проводится статистическими методами, позволяющими оптимизировать процедуру обработки и анализа эксперимента. Используя активный (спланированный) эксперимент, можно достичь существенно большего — оптимизировать и стадию постановки эксперимента. Под планированием эксперимента понимают оптимальное управление экспериментом в условиях неполной информации о механизме процесса. Развитие этой концепции связано с работами Р. Фишера, главная идея которых состоит в раздельной оценке эффектов в многофакторной ситуации. Широко применяемое планирование эксперимента при поиске оптимальных условий процесса связано с работами Бокса и Уилсона. В настоящее время методы планирования и оптимизации эксперимента широко применяются при изучении процессов в лабораторных и полузаводских условиях и несколько реже в промышленности.