1.4.2 Функция выживания и ее связь с функцией распределения

Пусть испытанием является наблюдение за компонентами РАС в течение какого-то выбранного исследователем промежутка времени. При этом начало наблюдения определяется неким фактом, в частности атака на РАС. Контролируемое событие – прекращение выполнения возложенных функций на наблюдаемый компонент вследствие успешной атаки злоумышленника, («смерть» компоненты) – является случайным событием. Время от начала наблюдения до «смерти» – случайная величина. Обозначим ее Т, тогда значения этой случайной величины – t. Вполне естественно, что введенная случайная величина неотрицательная и непрерывная, имеет свой закон распределения, априори неизвестный. Функция распределения случайной величины равна

где F(t) – вероятность не «дожить» до момента времени t от начала отсчета. При t<0 обязательно F(t) = 0, а при положительном аргументе F(t) – функция возрастающая (точнее, неубывающая), с ростом t стремящаяся к 1. Примерный вид графика функции F(t) представлен на рисунке 2.

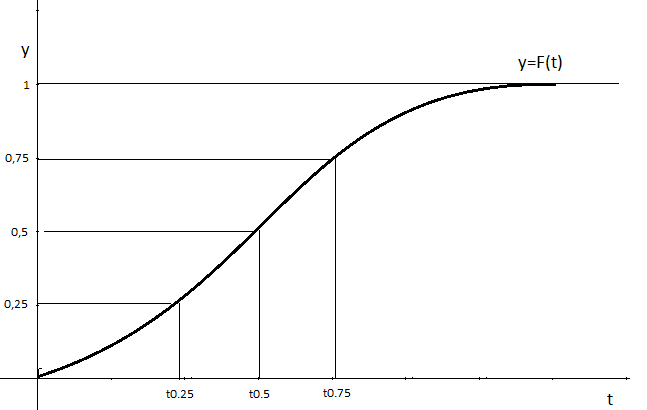
Рисунок 2 – Вид графика функции распределения F(t)

На рисунке (2) отмечены характеристики распределения: t_0.5 – медиана распределения, и t_0.25 , t_0.75 – нижняя и верхняя квартили.

Таким образом, функция распределения F(t) служит вероятностной характеристикой рассматриваемого процесса. По функции распределения F(t) можно найти соответствующую плотность распределения вероятностей f(t) как производную f(t) = F’(t).

Однако обычно исследуемый процесс времени «жизни» целесообразнее связывать не с функцией распределения F(t), а с дополняющей до единицы функцией

(1.24)

так как

). (1.25)

Согласно свойству вероятностей противоположных событий, то S(t) – вероятность штатного (с сохранением основных функций) функционирования компоненты РАС по истечении момента времени t с начала активного дестабилизирующего воздействия (прожить время, большее T).

Функцию S(t) заданную соотношениями (1.24) и (1.25), называют функцией «выживания» (выживаемостью).

Кривая функции «выживания» S(t) легко может быть построена исходя из графика функции распределения F(t) и соотношения (1.25). Стоит также отметить, что для функции S(t) значения функции при t<0 не имеют смысла. Соответствующий вид графика представлен на рисунке 3.

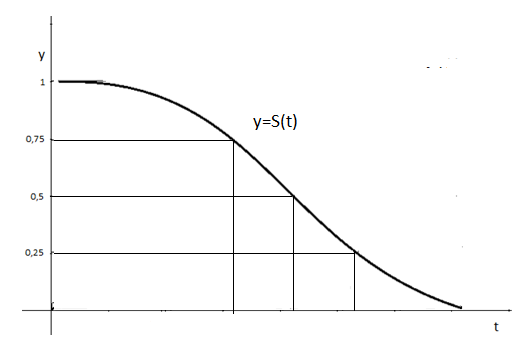
Рисунок 3 – Вид графика кривой выживаемости S(t)

Для удобства вычислим функцию выживания:

(1.26)

определяющую вероятность быть «живым» в момент времени t, или в более широком смысле, вероятность того, что исследуемое событие не наступило к моменту времени t [62].

График функции y=S(t) называют [90] кривой выживаемости. Значение, при котором S(τ_0.5)=0,5 называется медианой выживаемости. Легко заметить, что медиана выживаемости совпадает с медианой распределения случайной величины Т. Медиана выживаемости является одной из важнейших характеристик выживаемости: она указывает середину теоретического времени жизни отдельного компонента системы после начала отсчета (в качестве начала отсчета может быть рассмотрена активная фаза атаки на компоненты РАС) [22-25]. Аналогично квантилям распределения порядка р, где 0<p<1, обозначаемым t_p, используют квантили выживаемости. Обозначим квантиль выживаемости порядка р посредством τ_р, где S(τ_р)=p. Тогда для квантилей выживаемости и соответствующих квантилей распределения справедливо соотношение

τ_р=t_1-p, (1.27)

т.е. квантиль выживаемости порядка р является квантилью распеделения порядка 1-р. Соотношение (1.27) можно легко доказать: согласно (1.26) получаем

,

следовательно

Таким образом, значение распределения случайной величины Т порядка (1-р).

Кривая выживаемости y=S(t), построенная по распределению случайной величины Т является теоретической кривой, характеризующей процесс продолжительности «жизни». Соответствующие характеристики выживаемости согласованы с вероятностным распределением, т.е. базируются на вероятностной основе[47].

При этом, значения квантильной широты, определяемой как расстояние между двумя точками (квантилями), в обоих случаях совпадают:

Возможно охарактеризовать величины Т с помощью функции риска- мгновенной интенсивности осуществления события

(1.28)

В числители этого выражения (1.28) находится условная вероятность того, что событие произойдет в интервале времени ( , + ), если оно не произошло ранее, а знаменатель – ширина интервала. Разделив одно на другое, получаем интенсивность осуществление события в единицу времени. Устремляя ширину интервала к нулю и переходя к пределу, получаем мгновенную интенсивность осуществления события[68].

Условную вероятность в числителе можно записать в виде отношения совместной вероятности того, что Т принадлежит интервалу ( , + ) и (что совпадает с вероятностью того, что Т принадлежит указанному интервалу), к вероятности условия . Первая из них равна для малого а последняя это , по определению. Деление на и предельный переход дают следующий результат:

(1.29)

который и является определением функции риска. Интенсивность осуществления события в момент времени равна плотности событий в момент , деленной на вероятность дожить до этого момента, не испытав событие ранее[77].

Учитывая, что - это производная уравнение (1.29) можно записать в виде

Если теперь проинтегрировать обе части от 0 до и ввести граничное условие (поскольку событие не может произойти к моменту времени 0), можно преобразовать приведенное выражение и получить формулу для вероятности работоспособности компонента РАС (вероятности «дожить») до момента времени t как функции от рисков во все моменты времени до t:

(1.30)

Интеграл в фигурных скобках в этом уравнении называют [13] кумулятивным риском, обозначим его как

который можно рассматривать как сумму всех рисков при переходе от момента времени 0 к t, т.е. интегральным риском.

Фактически функции выживания и риска дают альтернативные, но эквивалентные описания распределения величины Т. Имея функцию выживания, можно ее продифференцировать и получить функцию плотности, а затем найти функцию риска. Зная функцию риска, можно ее проинтегрировать и получить кумулятивный риск, а затем от нее экспоненту и найти функции выживания, используя уравнение (1.30) [28].

Для задач с дискретным временем всегда определены вероятности

В дискретном случае риск можно определить по формуле:

где и

Риск может быть любой неотрицательной функцией, в случае дискретного времени не превосходящей 1, выживаемость - неотрицательной, начинающейся со значением 1 и монотонно невозрастающей, а условие = 0 равносильно расходимости интеграла при непрерывном времени или ряда при дискретном.

Для системы из n объектов с разными распределениями времени жизни { } и соответственно, функциями выживаемости { } можно определить усредненную функцию выживаемости, равную математическому ожиданию доли объектов, выживших к моменту t:

Плотность и функция распределения получившегося «усредненного» объекта также равны средним арифметическим соответствующих функций индивидуальных объектов[124].