3. Вероятностные оценки уязвимости и безотказности

Используем некоторые понятия и определения [22,30,32]:

Надежность – свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения, установленных эксплуатационных показателей.

Отказ—это частичная или полная утрата свойств элемента, которая существенным образом снижает или приводит к полной потере работоспособности. Отказ наступает всякий раз, когда устройство не сохраняет своих параметров в заданных пределах.

Система работоспособна, если она нормально выполняет заданные функции и ее основные параметры находятся в пределах нормы. Утрата работоспособности означает отказ.

Система – греч. systema – целое, составленное из частей; соединение – множество элементов, находящихся в отношениях и связях друг с другом, образующие определенную целостность, единство.

Элемент — это некоторый объект (материальный, энергетический, информационный), обладающий рядом важных свойств, реализующий определенную функцию системы, внутренняя структура которого не рассматривается.

Опираясь на них, осуществим исследования. Пусть исследуется выход из строя системы после атаки. При этом наблюдение начинается с момента проведения атаки. Наблюдаемое событие – выход из строя всей системы вследствие успешной реализации атаки. Ввиду того что мы не знаем когда произойдет отказ системы событие является случайным. Время от начала наблюдения до выхода системы из строя – случайная величина.

Пусть имеется совокупность элементов, каждый из которых характеризуется неотрицательной случайной величиной Т, называемой длительностью его безотказной работы. Длительность безотказной работы будет «возрастом» элемента к моменту, когда произойдет отказ. Случайная величина Т является неотрицательной и имеет дискретное или непрерывное распределение, закон распределения априори неизвестный.

Практический интерес представляет второй случай, когда время безотказной работы имеет непрерывное распределение. По определению [5] функцией распределения (интегральным законом распределения) случайной величины Т называется функция {Т<=t}, определяемая как вероятность того, что элемент отказал до момента t. Для целей расчета надежности удобнее пользоваться функцией, дополнительной к F(t) и называемой вероятностью безотказной работы P(t). Эта функция задает вероятность того, что элемент не откажет до момента времени t. Очевидно, что {Т > t}, Р(0)=1, Р(1)=0 и является невозрастающей функцией времени.

Вероятность исправной работы компонент системы [4] равна

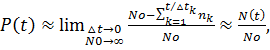(1.1)

где – число компонент вначале испытаний; n_k – число компонент, которые вышли из строя в интервале времени △t_k; t — время, для которого определяется вероятность исправной работы; △t_k — принятая продолжительность интервала времени наблюдения; — число элементов, исправно работающих в интервале

[0, t]. Вероятность отказа очевидно равна

(1.2)

Согласно (1.1) она может быть определена следующим образом

(1.3)

Среднее время безотказной работы. Под этим термином в теории надежности [78] понимается математическое ожидание времени исправной работы:

(1.4)

Из (1.1) среднее время исправной работы однотипных объектов равно

(1.5)

где —число элементов, над которыми проводятся испытания; — время исправной работы k-го компонента. Так как трудно определить , удобнее будет пользоваться другим выражением:

(1.6)

где t—время, в течение которого вышли из строя все компоненты; △ —величина интервала времени.

Величина позволяет определить количество «выживших» после атаки элементов системы, но полностью не характеризует ее надежность.

Рассмотрим аналитическую зависимость между приведенными характеристиками. Пусть Т—время непрерывной исправной работы от начала до отказа; t—время, в течение которого надо определить вероятность исправного функционирования системы P(t). Вероятность, того, что за время t произойдет хотя бы один отказ, равна

(1.7)

Вероятность того, что за время t не произойдет отказа, соответственно равна

(1.8)

(1.9)

Следовательно, среднее время функционирования системы есть математическое ожидание случайной величины:

(1.10)

тогда из (1.9) получаем

(1.11)

Интегрирование по частям

( 1.12)

(1.13)

Число элементов, которые будут работать непрерывно к моменту t, определяется из (1.1) следующим образом

(1.14)

За интервал △t число отказавших элементов составит

(1.15)

Функцию S(t) (1.2) называют [13] функцией работоспособности системы.

В теории вероятностей функция риска (интенсивность) непрерывной случайной величины определяется [78] соотношением:

(1.16)

где