3.3.2. Статистические характеристики случайной величины
Построение гистограммы
Гистограммой называют график, который является выборочной оценкой функции плотности распределения вероятности, которую можно получить по выборочным данным. При построении гистограммы область значений случайной величины разбивается на несколько подынтервалов, а затем подсчитывается процент попадания исходных значений случайной величины в выбранные подынтервалы. Для построения гистограммы имеется несколько встроенных функций:
Гистограмма с произвольными сегментами разбиения.
Процедура hist(intvls,x) определяет вектор частоты попадания данных в интервалы гистограммы; intvls – вектор, элементы которого задают сегменты построения гистограммы в порядке возрастания; х – вектор случайных данных.
Пример (рис.22)
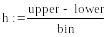
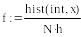
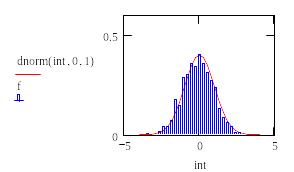
Рис.22
Для анализа взято 1000 данных с нормальным законом распределения, созданных генератором случайных чисел. Далее определяются границы интервала (lower,upper), содержащего внутри себя все значения случайной величины. Далее осуществляется разбиение этого интервала на bin одинаковых сегментов, начальные точки которых записываются в вектор int.
2. Гистограмма с разбиением на равные сегменты
Если нет необходимости задавать сегменты гистограммы разной ширины, то удобнее воспользоваться упрощенным вариантом функции hist.
Пример (рис.23).
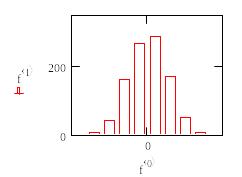
Рис.23
Создание графика гистограммы
Для того, того чтобы построить график в виде гистограммы необходимо (рис.24):
Построить двумерный график, задать переменные по осям и пределы оси ОХ.
Войти в диалоговое окно «Форматирование графика» и перейти на вкладку «След».
Установить для серии данных гистограммы в поле «Тип» элемент списка bar (столбцы) или solidbar (гистграмма).
Нажать кнопку «ОК».
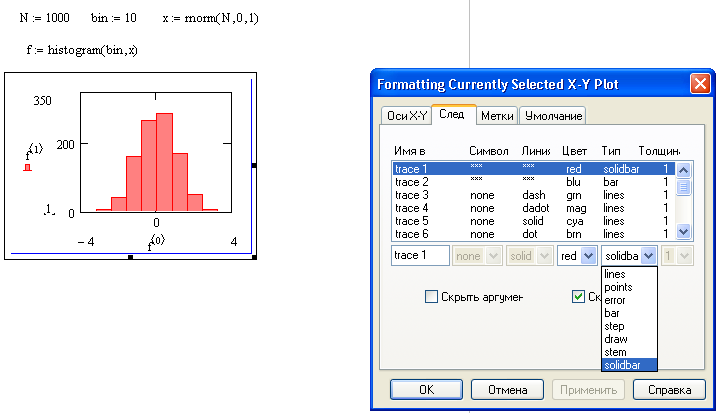
Рис.24
Вычисление оценок числовых характеристик случайной величины
Mathcad имеет ряд встроенных функций для расчетов числовых характеристик ряда случайных данных.
К ним относятся вычисление:
- выборочного среднего - mean(x);
- выборочной медианы – median(x);
- выборочной дисперсии - Var(x);
- выборочного среднеквадратичного отклонения - stdev(x);
- максимального и минимального значений выюорки -max(x), min(x);
- наиболее часто встречающего значения выборки - mode(x).
Рассмотрим пример расчета числовых характеристик в среде Mathcad.
Пример.
Числовые характеристики приведены для случайной величины, распределенной по закону Вейбулла. Отметим, что медиана не совпадает со средним значением. Это связано с несимметричностью этого закона.
Использование встроенных функций для вычисления оценок различных числовых характеристик случайной величины рассмотрим на конкретных примере.
Пример.
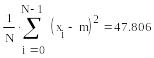
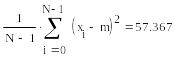
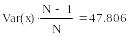
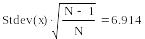
