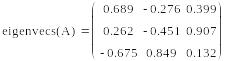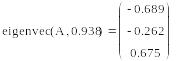7. Число обусловленности квадратной матрицы

Важнейшей характеристикой квадратной матрицы является число обусловленности. Число обусловленности является мерой близости матрицы к вырожденности.

Чем больше число обусловленности, тем ближе матрица вырожденности, минимальное число обусловленности равно 1. Вычисление числа обусловленности осуществляется с помощью диалогового окна (рис.16) и вычисляется по-разному для различных типов норм матрицы:

cond1(A) – для norm1(A);

cond2(A0 – для norm2(A);

conde(A) – для norme(A);

condi(A) - для normi(A).

Рассмотрим примеры вычисления числа обусловленности.

Примеры.

8. Ранг матрицы

Рангом прямоугольной матрицы называют наибольшее число независимых строк или столбцов матрицы. Для вычисления ранга предназначена функция rank.

Обращение к этой функции происходит с помощью диалогового окна (рис.16).

Пример.

3.2.2. Решение систем линейных уравнений

Важнейшей задачей линейной алгебры является решение системы линейных алгебраических уравнений (СЛАУ).

СЛАУ имеет единственное решение, если матрица системы является невырожденной (или не сингулярной), то есть ее определитель не равен нулю. В среде Mathcad существует несколько способов решения СЛАУ. Наиболее распространенным является использование встроенной функции isolve(A,b), где A- это матрица коэффициентов системы, а b – столбец свободных членов этой системы. Доступ к этой функции осуществляется через кнопку f(x), расположенной на панели инструментов и через диалоговое окно (рис.16).

Рассмотрим пример решения СЛАУ.

Пример.

1.

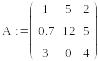
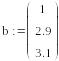2.

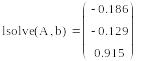
3.2.3. Собственные числа и собственные векторы матриц

Второй наиболее часто встречающейся задачей линейной алгебры является задача поиска собственных чисел и собственных векторов заданной квадратной матрицы. Нахождение собственных чисел эквивалентно задаче решения СЛАУ вида:

Эта однородная система линейных уравнений имеет решения для конкретных значений - λ₁, λ₂,…., которые называются собственными числами матрицы системы А. Каждому собственному числу соответствует собственный вектор – х₁, х₂,….., который является решением системы для данного собственного числа. Таким образом, для того, чтобы знать полный набор решений, необходимо определить собственные числа матрицы системы и найти для них соответствующие собственные векторы.

Для решения таких задач на собственные числа и собственные векторы существует несколько встроенных функций, реализующих достаточно сложные вычислительные алгоритмы:

- eiganvals(A) – вычисляет вектор собственных чисел;

- eigenvecs(A) – вычисляет матрицу, содержащую нормированные собственные векторы, каждый столбец включает в себя координаты одного собственного вектора, количество столбцов равно количеству собственных чисел;

- eigenvec(A,λ) – вычисляет один собственный вектор для заданного собственного числа.

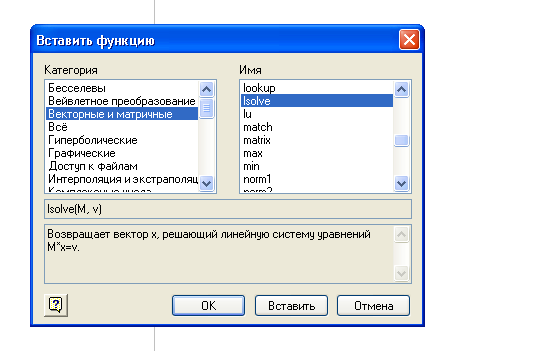
Доступ к этим функциям осуществляется через панель инструментов и диалоговое окно (рис.16):

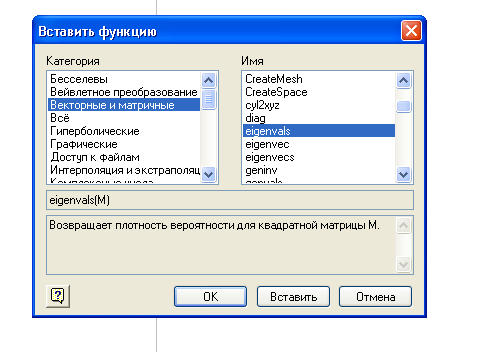
Проиллюстрируем применение этих функций на примерах.

Примеры.