3.3.3. Ковариация и корреляция
Степень связи между парами случайных векторов определяют коэффициенты ковариации и корреляции.
Коэффициент корреляции – это нормированный коэффициент ковариации. Mathcad имеет следующие функции, определяющие эти коэффициенты:
- corr(x1,х2) – коэффициент корреляции двух случайных векторов;
- cvar(x1,х2) – коэффициент ковариации двух случайных векторов.
Рассмотрим действие этих функций на примере.
Пример.
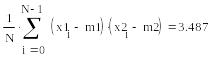
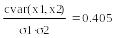
3.3.4. Генерация коррелированных случайных чисел
Для ряда статистических задач требуется генерация случайных величин с определенной корреляцией. Рассмотрим пример работы программы, создающей два вектора одинакового размера и одним и тем же распределением, случайные элементы которых попарно коррелированны с заданным коэффициентом корреляции R.
Пример.
Результат действия программы для коэффициента корреляции, равного 0.451, проиллюстрирован на рис.24.
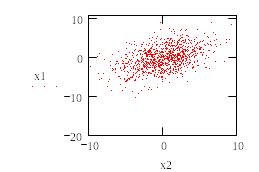
Рис.24
3.3.5. Интервальное оценивание
Интервальное оценивание числовых характеристик случайной величины также может быть получено с помощью встроенных функций. Рассмотрим в качестве примера интервальное оценивание дисперсии нормально распределенной случайной величины с нулевым математическим ожиданием и единичной дисперсией по выборке объемом 50.Требуется определить числовой интервал (L,U), внутри которого будет лежать значение дисперсии с вероятностью
Эта задача в статистике решается с помощью χ2 - распределения. Приведем листинг этих расчетов.
Пример.
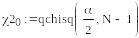
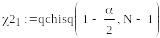
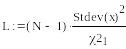
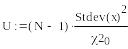
Таким образом, значение дисперсии с 75%-ной доверительной вероятностью лежит в пределах от 0.717 и 1.146. Указанный интервал называется 75%-ным доверительным интервалом.
3.3.6. Проверка статистических гипотез
В математической статистике проверка статистических гипотез является ключевой задачей. В качестве примера рассмотрим проверку гипотезы о математическом ожидании при неизвестной дисперсии для нормально распределенной случайной величины, представленной выборкой объемом N=60. Требуется принять или опровергнуть гипотезу о том, что математическое ожидание равно μ0=0.2. Вероятность ошибочного отклонения истинной гипотезы (гипотезы того, что математическое ожидание равно 0.2) задается и равна α=0.1.
Для этой задачи используется распределение Стьюдента, функция которого также представлена в среде Mathcad.
Пример.
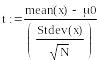
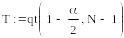
В последней строке вычисляется истинность или ложность условия, выражающего решение задачи. Поскольку условие оказалась ложным (то есть равным 0), то гипотезу необходимо отвергнуть.