3.2.4. Матричные разложения

Большинство методов решения систем линейных алгебраических уравнений основаны на матричном разложении. Как правило, после определенного разложения матрицы системы, нахождение решения существенно упрощается. Mathcad имеет несколько встроенных функций, реализующих наиболее популярные матричные разложения.

1. Разложение Холецкого.

Разложение Холецкого используется для симметричных матриц. Алгоритм Холецкого реализован во встроенной функции cholesky(A), A – квадратная, положительно-определенная матрица. Обращение к функции по-прежнему происходит с помощью панели инструментов и диалогового окна (рис.16).

Пример.

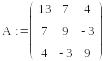
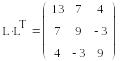
2. QR-разложение

Данное разложение имеет вид:

A=Q*R,

Q – ортогональная матрица, R – верхняя треугольная матрица.

Это разложение можно осуществить с помощью встроенной функции qr(A). Результат действия этой процедуры рассмотрим на примере.

Пример.

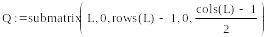
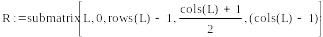
3. LU-разложение

LU-разложение (или треугольное разложение) – это матричное разложение, в результате которого исходная матрица может быть представлена произведением двух треугольных матриц :

A=L*U,

где L – нижняя треугольная матрица, а U - верхняя треугольная матрица. Рассмотрим пример такого разложения.

4. Сингулярное разложение

Сингулярным разложением данной матрицы называется разложение вида:

U, V – ортогональные матрицы размером [nxn], s – диагональная матрица с сингулярными числами матрицы А на диагонали.

Процедурами, которые позволяют осуществить сингулярное разложение, являются:

-svds(A) – вектор, состоящий из сингулярных чисел;

-svd(A) – сингулярное разложение.

Пример.

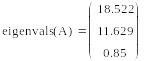
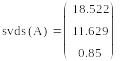
В результирующей матрице первые три строки представляют матрицу U, в остальные строки являются строками матрицы V.

3.3. Математическая статистика

3.3.1. Случайные величины

Для моделирования различных физических, экономических и прочих процессов часто бывает необходимым иметь случайные процессы и случайные величины с известными законами распределения. Mathcad имеет ряд встроенных функций, которые позволяют получать последовательность значений случайной величины по известному распределению. Таким образом, существует генератор случайных чисел, создающий выборку псевдослучайных данных с соответствующим законом распределения.

Пример.

Перечислим встроенные функции, которые рассчитывают числовые характеристики этого распределения:

- dnorm(x,m,σ) – плотность вероятности нормального распределения (рис.17);

- pnorm(x,m,σ) – функция нормального распределения (рис.18);

- cnorm(x) – фунция нормального распределения с нулевым математическим ожиданием и единичной дисперсией;

- qnorm(F,m,σ) – обратная функция нормального распределения;

- rnorm(M,m,σ) – вектор М независимых случайных чисел, каждое из которых имеет нормальное распределение.

x – значение случайной величины; Р – значение вероятности; m – математическое ожидание; σ – среднеквадратичное отклонение.

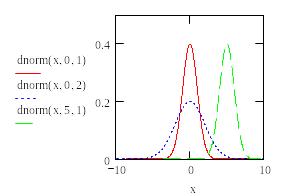
Рис.17

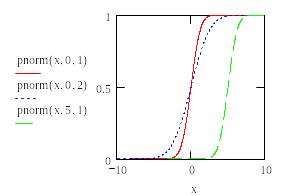
Рис.18

Функция распределения вероятностей F(x) – это вероятность того, что случайная величина примет значение меньшее или равное х. Функция, обратная F(x), называемая квантилем распределения, позволяет по заданному аргументу р определить значение х так, что случайная величина будет меньше или равна х с вероятностью р.

Приведем несколько примеров использования рассматриваемых функций.

Пример 1. Вероятность того, что случайная величина примет значение меньше 1.5.

Пример 2. Нахождение 95%-ного квантиля нормального распределения.

Пример 3. Вероятность того, что значение случайной величины будет больше 1.

Пример 4.Вероятность того, что значение случайной величины находится в интервале (2,3).

Пример 5. Вероятность того, что -2<x<2.

Пример 6. Вероятность того, что значение случайной величины находится в интервале (2,3) для случая нормального распределения с ненулевым математическим ожиданием и произвольной дисперсией.

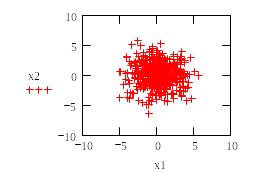
Пример 7. Генерация двух векторов с нормальным законом распределения (m -математическое ожидание, σ - среднеквадратичное отклонение распределения). Размерность векторов равна 500. На рис.19 изображено распределение полученных точек на плоскости.

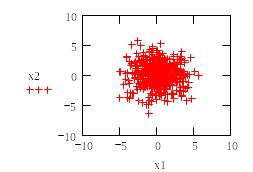
Рис.19

Равномерное распределение

Равномерное распределение – это распределение с постоянной вероятностью:

Приведем список встроенных функций это распределения:

- dunif(x,a,b) – плотность вероятности равномерного распределения;

- рunif(x,a,b) – функция равномерного распределения;

- qunif(P,a,b) – квантиль равномерного распределения;

- runif(M,a,b) – вектор М независимых случайных чисел;

- rnd(x) – случайное число, имеющее равномерную плотность распределения на интервале (0,x) ;

х – значение случайной величины, Р – значение вероятности, (a,b) – интервал, на котором случайная величина распределена равномерно.

Действие этих функций аналогично действию соответствующих функций нормального распределения.

Биномиальное распределение

Одним из наиболее известных распределений дискретной случайной величины является биномиальное распределении. Приведем основные встроенные функции этого распределения:

- dbinom(k,n,p) – плотность вероятности биномиального распределения;

- pbinom(k,n,p) – функция биномиального распределения (рис.;

- qbinom(Р,n,p) – квантиль биномиального распределения;

- rbinom(М,n,p) – вектор М независимых случайных чисел, каждое из которых имеет биномиальное распределение;

к – дискретное значение случайной величины; Р – значение вероятности; n – параметр распределения (количество независимых испытаний); р – параметр распределения (вероятность единичного случайного события. Примеры биномиального распределения представлены на рис.20.

Другие статистические распределения

Mathcad включает в себя и другие типы распределений. Встроенные функции этих распределений можно посмотреть в категории «Плотность вероятности» диалогового окна «Вставить функцию», которое открывается при нажатии на кнопку .

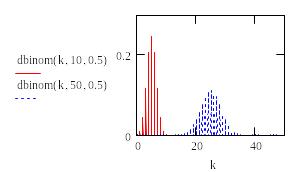
Рис.2