5. Реализация билинейного преобразования

Билинейное преобразование –  конформное отображение, используемое для того, чтобы преобразовать передаточную функцию   линейной стационарной системы (корректирующие звенья систем управления, электронные фильтры и т. п.) из непрерыв-ной формы в передаточную функцию   линейной системы в дискретной форме. Оно отображает точки jω-оси,  , на s-плоскости в окружность единичного радиуса,  , на z-плоскости.

Это преобразование сохраняет устойчивость исходной непрерывной системы и существует для всех точек её передаточной функции. То есть для каждой точки передаточной функции или АФЧХ исходной системы существует подобная точка с идентичной фазой и амплитудой дискретной системы. Однако эта точка может быть расположена на другой частоте. Эффект сдвига частот практически незаметен при небольших частотах, однако существенен на частотах, близких к частоте Найквиста.

Билинейное преобразование представляет собой функцию, аппроксимирующую натуральный логарифм, который является точным отображением z-плоскости на s-плоскость. При взятии преобразования Лапласа над дискретным сигналом  (представляющего последовательность отсчётов), результатом является Z-преобразование с точностью до замены переменных:

(5.1)

где T – период квантования (обратная к частоте дискретизации величина).

Аппроксимация, приведённая выше, и является билинейным преобразованием.

Обратное преобразование из s-плоскости в z-плоскость и его билинейная аппроксимация записываются следующим образом:

    (5.2)

Билинейное преобразование использует это соотношения для замены передаточной функции   на её дискретный аналог:

(5.2)

то есть:

(5.3)

Частота дискретизации выбирается в 10..100 раз больше максимальной частоты.

Для того чтобы не происходило переполнение сумматоров при работе программы фильтра в МК, произведем нормирование передаточной функции на максимальное значение АЧХ. Пересчитаем граничные частоты цифрового фильтра в граничные частоты прототипа. Граничная частота:

(5.4)

Далее, применив Z-преобразование к передаточной функции аналогового фильтра H(s), получим передаточную функцию цифрового фильтра H(z):

, (5.5)

где fd – частота дискретизации.

После подстановки (5.5) в (3.1-3.3), получим следующие выражения для функций звеньев фильтра.

Для функций Баттерворта, Чебышева и Бесселя функция звена второго порядка:

(5.6)

Для инверсных Чебышева и эллиптических функция звена второго порядка:

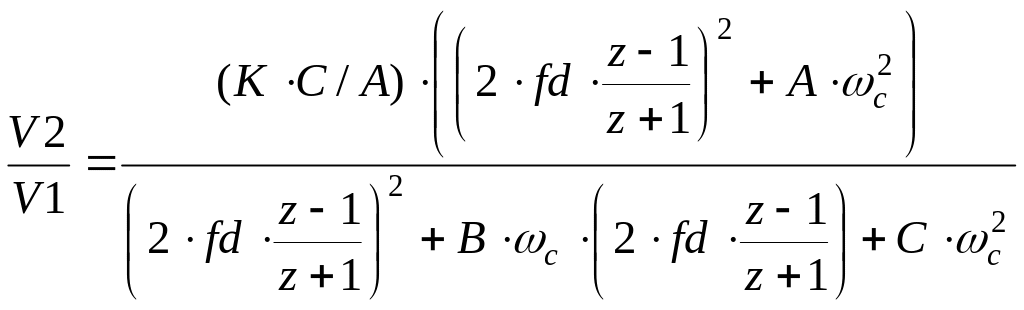(5.7)

Функция звена первого порядка фильтров типа Чебышева, инверсного Чебышева, Баттерворта, Бесселя и эллиптического:

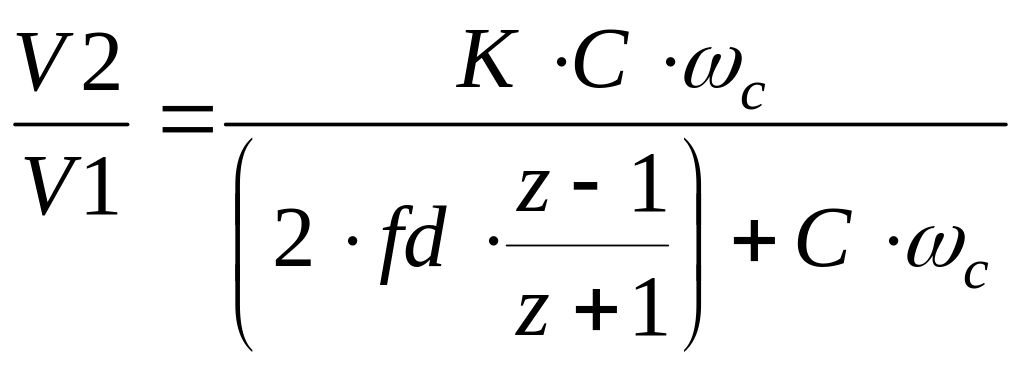(5.8)

Затем, после упрощений и перераспределения слагаемых, определим коэффициенты цифрового фильтра при , где k= 0, 2, 4..n (где n – четно).

Таким образом, после нахождения новых коэффициентов уже цифрового фильтра, можно построить АЧХ и ФЧХ его звеньев и всей передаточной функции аналогично тому, как это было сделано для аналогового в пункте 3.

6. Корректировка коэффициентов

Для того, чтобы удовлетворить требованиям разрядность МК и избежать переполнения сумматоров, учесть разницу в коэффициентах в 2 порядка, обеспечить приемлемую точность вычислений, с полученными коэффициентами следует произвести некоторые эквивалентные преобразования.

Допустим, мы имеем дело с МК, разрядность которого m. Для соблюдения вышеобозначенных требований вводим масштабирующий коэффициент:

Тогда нормирующий коэффициент определим как:

,

где b1 является коэффициентов при z⁰ в знаменателе передаточной функции звеньев. Далее происходит корректировка всех остальных коэффициентов данного звена по формуле:

Критерий верности, который должен постоянно соблюдаться при этом процессе, является: .

После нормировки всех коэффициентов строятся частотные характеристики нормированного фильтра и сравниваются с аналогичными характеристиками аналогового фильтра-прототипа. На основе этих сравнений можно сделать вывод о пригодности/ непригодности МК с данной разрядность.

В заключении предлагается задать в среде Mathcad сигнал, линейно изменяющийся по частоте (0… fd/2) , и пропустить его через полученный цифровой фильтр.

Осуществляется это исходя из определения передаточной функции фильтра, которое для z-образов сигналов будет иметь вид:

H(z)=V2(z)/V1(z), где V1(z) и V2(z) – z-образы входного и выходного сигнала соответственно.

Фильтрацию входного сигнала осуществляют последовательно для каждого звена. Причем в качестве входного сигналы каждого последующего звена используют выходной сигнал предыдущего.

, (6.1)

где Y_i – функция на выходе звена, i – порядок звена, j – порядок отсчета входного сигнала

В качестве наглядно примера прилагается решение одного варианта домашнего задания по указанному алгоритму.