Московский государственный технический университет
имени Н.Э. Баумана
Факультет «Биомедицинская техника»
А.Е. Косоруков
Методическое пособие
для выполнения домашнего задания по дисциплине МПАСиК
8 семестр.
Электронное учебное издание
Москва
(С) 2012 МГТУ им. Н Э Баумана
УДК &&&
Косоруков А. Е.
Методическое пособие для выполнения домашнего задания по дисциплине МПАСиК. Электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2012. 29с.
%%%%В данном пособии рассматриваются основные характеристики активных фильтров на операционных усилителях и методы расчета передаточных функций аналоговых и цифровых фильтров.
Методические указания предназначены для студентов 4-го курса, изучающих дисциплину «Медицинские приборы, аппараты и системы»
Электронное учебное издание
Косоруков Артем Евгеньевич
Методическое пособие для выполнения домашнего задания по дисциплине мпаСиК
8 Семестр.
© 2012 МГТУ имени Н.Э. Баумана
Содержание
Методическое пособие 1
для выполнения домашнего задания по дисциплине МПАСиК 1
8 Семестр. 1
Методическое пособие для выполнения домашнего задания по дисциплине МПАСиК. Электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2012. 29с. 2
Методическое пособие 2
для выполнения домашнего задания по дисциплине МПАСиК 2
8 Семестр. 2
1. Введение 5
2. Определение порядка фильтра 7
3. Определение коэффициентов 8
4. Построение АЧХ и ФЧХ отдельных звеньев и всего фильтра по найденным коэффициентам 9
5. Реализация билинейного преобразования 10
6. Корректировка коэффициентов 12
7. Порядок выполнения работы 14
9. Пример расчета фильтра 16
9.1. Определение порядка фильтра и коэффициентов 16
9.2. Построение АЧХ и ФЧХ звеньев 18
9.3.Реализация билинейного преобразования 19
9.4. Нормировка коэффициентов и построение АЧХ и ФЧХ цифрового фильтра 22
9.5. Фильтрация линейно изменяющегося сигнала. 26
Список литературы 31
1. Введение
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. То есть он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами фильтров являются фильтра нижних частот (пропускают низкие частоты), фильтры высоких частот (пропускают высокие частоты), полосно-пропускающие и полосно-заграждающие фильтры.
Более точно характеристику частотно-избирательного фильтра описывает его передаточная функция:
(1.1)
где величины V1 и V2 представляют собой соответственно входное и выходное напряжение.
Для установившейся частоты s=jω передаточную функцию можно записать в виде:
(1.2)
где |H(jω)| − модуль передаточной функции или амплитудно-частотная характеристика (АЧХ); φ(ω) – фазо-частотная характеристика.
Рис.1.1. Изображение электрического фильтра.
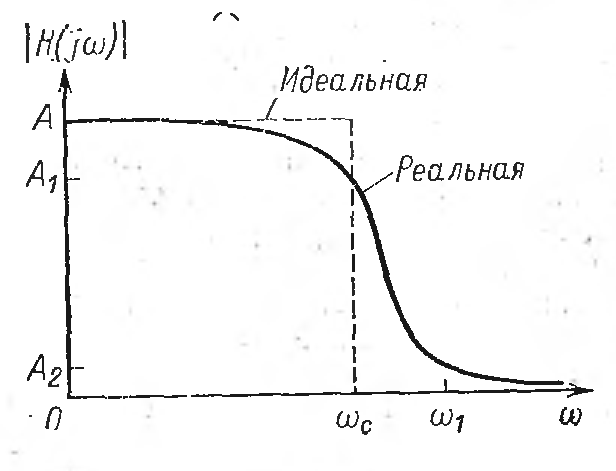
Рис.1.2. Идеальная и реальная амплитудно-частотные характеристики ФНЧ.
В качестве примера на рис.1.2 показаны пунктиром идеальная АЧХ ФНЧ, которая за частотой среза ωс равна нулю и постоянна на полосе пропускания. На практике такое реализовать невозможно, так как следует реализовать очень узкую переходную область, поэтому реальная АЧХ выглядит примерно так, как показано сплошной линией.
Следовательно, основная задача при конструировании фильтра заключается в приближении к идеальной реальной АЧХ с заданной степенью точности.
Всю частотную область под графиком функции на рис.1.2 условно можно поделить на три части: полосу пропускания (0<ω<ωc), полосу задержания (ω>ω1) и переходную область (ωc<ω<ω).
Значение амплитудно-частотной характеристики также можно выразить в децибелах (Дб) следующим образом:
(1.3)
И в этом случае α характеризует затухание. В основном, в полосе пропускания затухание никогда не превышает 3 Дб.
Передаточная функция реализуемого фильтра представляет собой отношение полиномов, которое можно записать в виде:
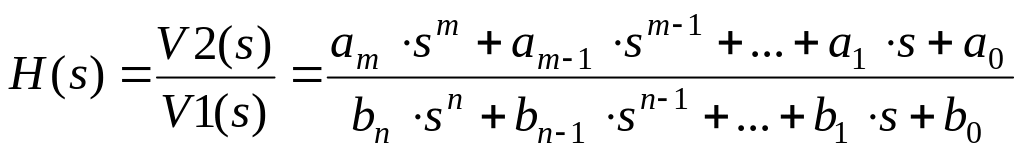(1.4)
Коэффициенты а и b – вещественные постоянные величины, m, n=1, 2, …(m≤n) (0.5)
Степень полинома знаменателя n определяет порядок фильтра. Как было отмечено ранее, не возможно добиться идеальной частотной характеристики, но с увеличением n добиваются максимального приближения АЧХ конструируемого фильтра к идеальной. Для наглядности можно рассмотреть зависимость вида АЧХ от порядка для 2-х видов фильтров: Баттерворта и Чебышева.
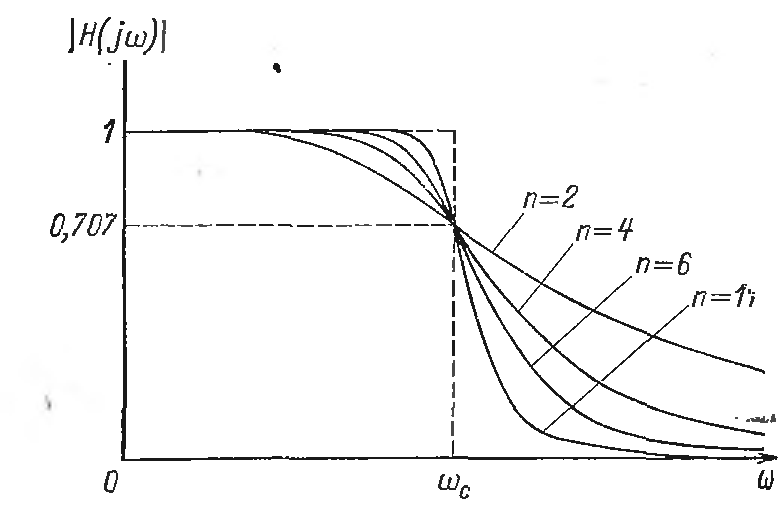
Рис.1.3. Амплитудно-частотные характеристики фильтра Баттерворта нижних частот.
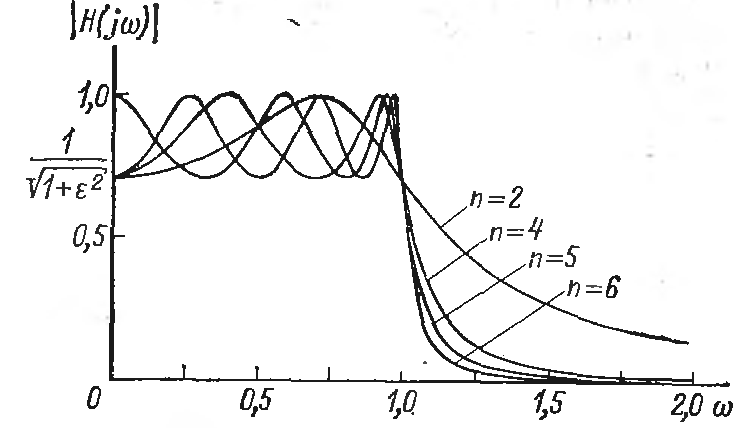
Рис.1.4. Амплитудно-частотные характеристики фильтров Чебышева нижних частот.