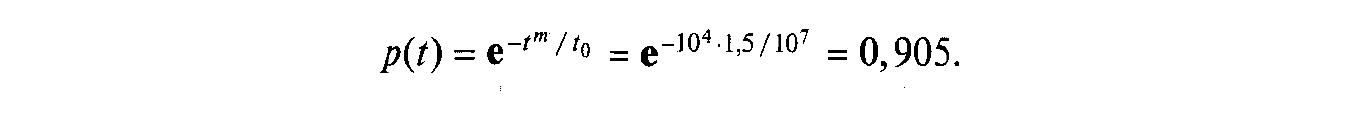- •Вища професійна освіта в. Ю. Шишмарев надійність технічних систем
- •Розділ 1: основні поняття теорії надійності
- •1.1 Основні терміни та визначення
- •1.2 Показники надійності
- •1.3 Випадкові величини та їх характеристики
- •1.4 Оцінка параметрів надійності
- •1.5 Різні періоди роботи технічних пристроїв
- •1.6 Надійність в період нормальної експлуатації
- •1.7 Надійність в період поступових відмов, що виникають через зношування і старіння
- •1.8 Спільна дія раптових і поступових відмов
- •1.9 Особливості надійності відновлюваних виробів
- •Глава 2
- •2 Надійність неремонтуємих об’єктів
- •2.1 Показники надійності неремонтуємих об’єктів
- •2.2. Теоретичні розподіли наробітку до відмови
- •Глава 3
- •3.1. Показники надійності ремонтованих об'єктів, не відновлюваних в процесі застосування
- •3.2. Показники надійності ремонтованих об'єктів, відновлюваних в процесі застосування
- •3.3. Ремонтопридатність і готовність технічних пристроїв
- •3.4. Методи випробування на надійність і статистичної обробки дослідних даних
- •Глава 4
- •4.1. Загальні відомості
- •4.2. Надійність систем з послідовно і паралельно з'єднаних елементів
- •4.3. Надійність послідовних систем при нормальному розподілі навантаження по однотипним підсистемам
- •4.5. Надійність систем з резервуванням
1.7 Надійність в період поступових відмов, що виникають через зношування і старіння
Для поступових відмов потрібні закони розподілу часу безвідмовної роботи, які дають спочатку низьку щільність розподілу, потім максимум і далі падіння, пов'язане із зменшенням числа працездатних елементів.
У зв'язку з різноманіттям причин і умов виникнення відмов в цей період для опису надійності застосовують кілька законів розподілів, які встановлюють шляхом апроксимації результатів випробувань або спостережень в експлуатації.
Нормальний
розподіл є найбільш універсальним,
зручним і широко застосовуваним для
практичних розрахунків (рис. 1.8 і 1.9).
Розподіл завжди підкоряється нормальному
закону, якщо на зміну випадкової величини
впливають багато приблизно рівнозначних
факторів (див. рис. 1.8,
![]() ).
Нормальному розподілу підпорядковується
напрацювання до відмови
).
Нормальному розподілу підпорядковується
напрацювання до відмови
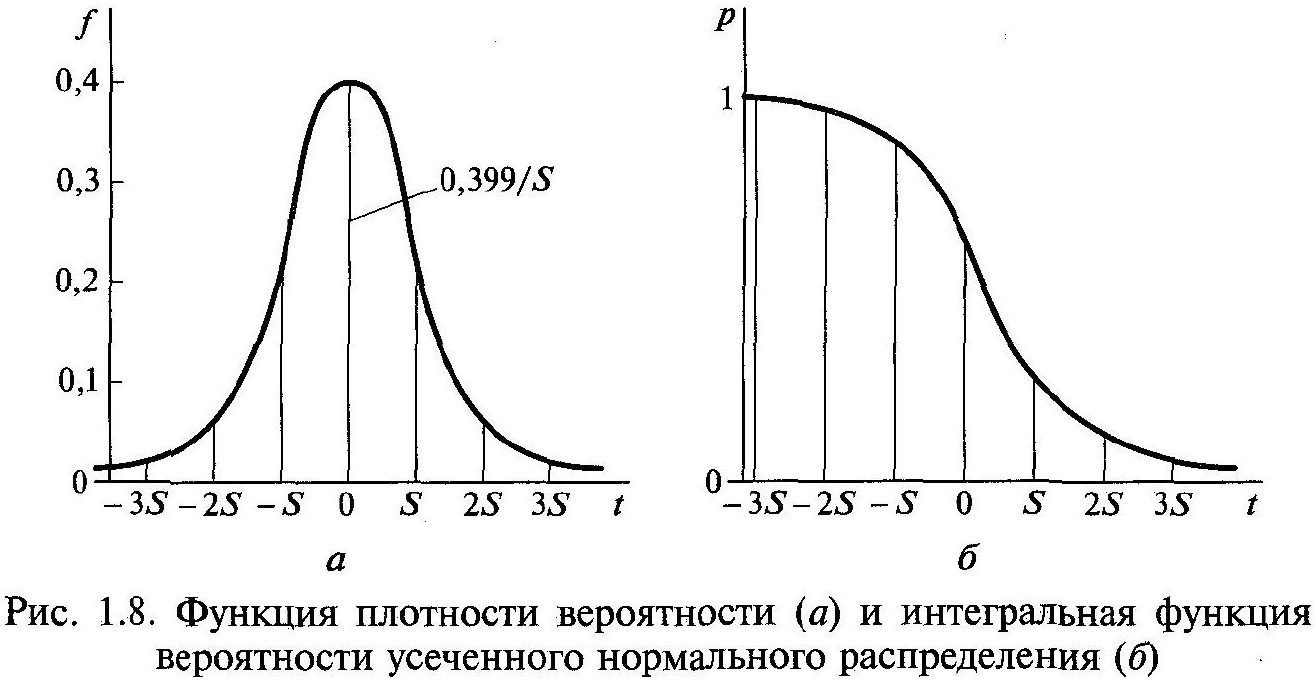
Рис. 1.8. Функція щільності ймовірності (а) і інтегральна функція ймовірності усіченого нормального розподілу (б)
багатьох відновлюваних та невідновлюваних виробів, розміри і помилки вимірювань деталей і т.д.
Щільність розподілу

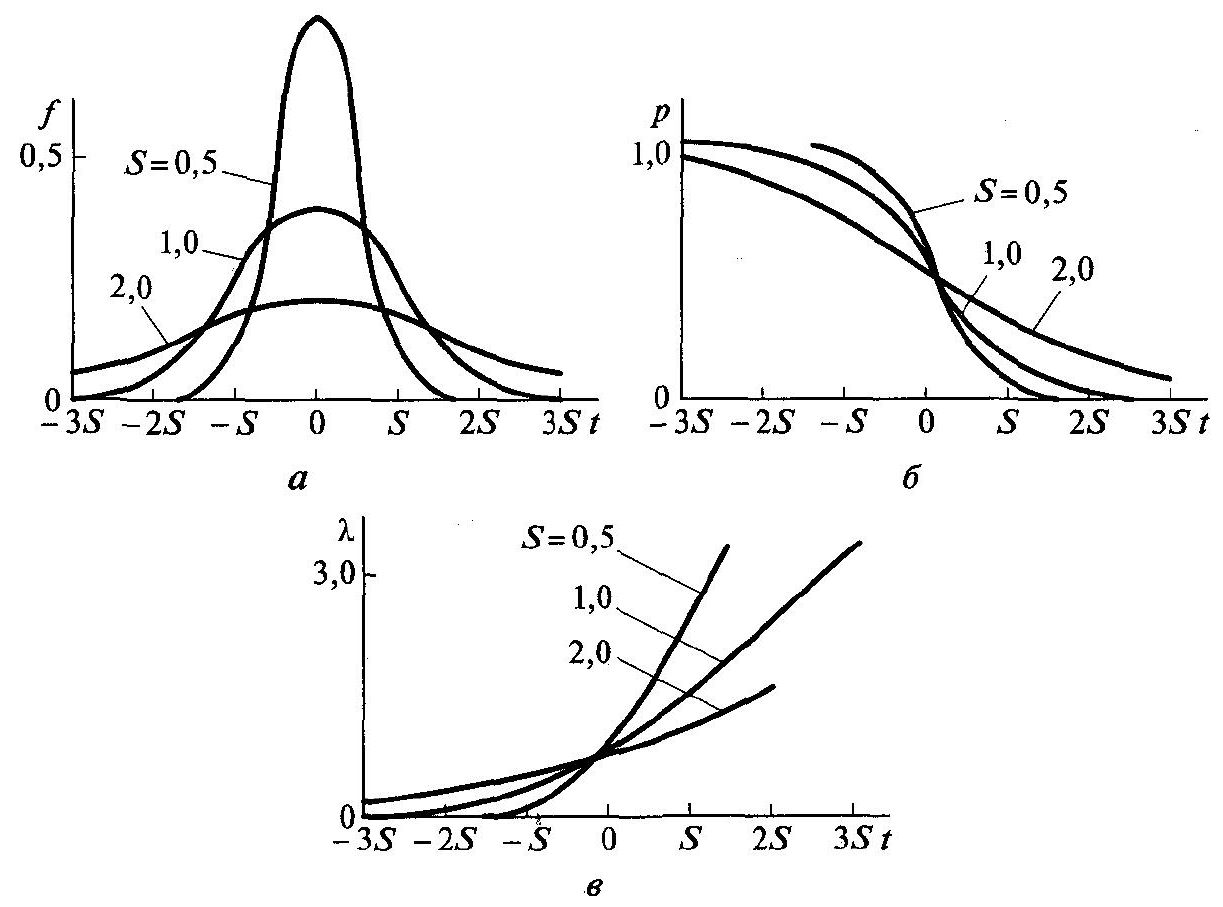
Рис. 1.9. Основні характеристики нормального розподілу при різних значеннях середнього квадратичного відхилення:
а
— щільність ймовірності
![]() ;
б — ймовірність безвідмовної роботи
;
б — ймовірність безвідмовної роботи
![]() ;
в — інтенсивність відмов.
;
в — інтенсивність відмов.
Розподіл
має два незалежних параметри: математичне
сподівання
![]() і середнє квадратичне відхилення
і середнє квадратичне відхилення
![]() Значення параметрів оцінюють за
результатами випробувань за наступними
формулами:
Значення параметрів оцінюють за
результатами випробувань за наступними
формулами:
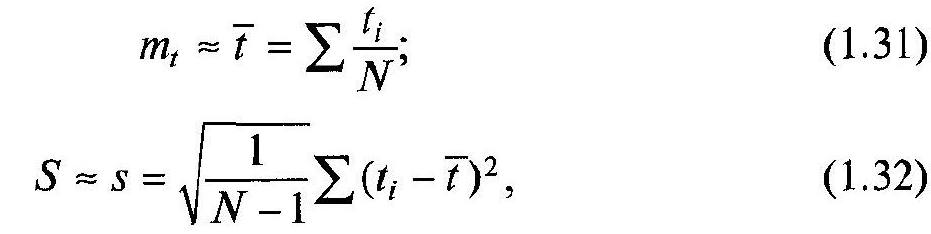
де
![]() — оцінка відповідно математичного
сподівання і середнього квадратичного
відхилення.
— оцінка відповідно математичного
сподівання і середнього квадратичного
відхилення.
Зближення
параметрів і їх оцінок збільшується зі
збільшенням числа випробувань. Іноді
зручніше оперувати з дисперсією
![]()
Крива
щільності розподілу тим гостріше і
вище, чим менше
![]() Вона починається від
Вона починається від
![]() і поширюється до
і поширюється до
![]() Це не є суттєвим недоліком, особливо
якщо
Це не є суттєвим недоліком, особливо
якщо
![]()
![]() так як площа, окреслена
прямуючими в нескінченність гілками
кривої щільності, що виражає відповідну
ймовірність відмов, дуже мала. Так,
ймовірність відмови за період часу
так як площа, окреслена
прямуючими в нескінченність гілками
кривої щільності, що виражає відповідну
ймовірність відмов, дуже мала. Так,
ймовірність відмови за період часу
![]() складає всього
складає всього
![]() і звичайно не враховується в розрахунках.
Імовірність відмови до
і звичайно не враховується в розрахунках.
Імовірність відмови до
![]() складає
складає
![]() .
Найбільша ордината кривої щільності
розподілу дорівнює
.
Найбільша ордината кривої щільності
розподілу дорівнює
![]() .
.
Інтегральна функція розподілу
![]()
Імовірність
відмови і ймовірність безвідмовної
роботи відповідно
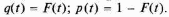
Замість
обчислення інтегралів за формулою
(1.33) зазвичай використовують таблиці.
Можна обійтися невеликими таблицями
для нормального розподілу, у якого
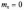 і
і
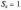 . Для
цього розподілу функція щільності
. Для
цього розподілу функція щільності

має
одну змінну
 Величина
Величина
 є центрованою, так як
є центрованою, так як
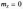 ,і
нормованою, так як
,і
нормованою, так як
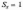 .
Функція щільності розподілу записується
у відносних координатах з початком на
осі симетрії петлі.
.
Функція щільності розподілу записується
у відносних координатах з початком на
осі симетрії петлі.
Функція розподілу являє собою інтеграл від щільності розподілу
![]()
З цього рівняння випливає, що
![]()
звідси
![]()
Для
використання таблиць слід застосовувати
підстановку

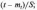 при цьому
при цьому
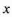 — квантиль нормованого нормального
розподілу і зазвичай позначається
— квантиль нормованого нормального
розподілу і зазвичай позначається
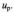
Щільність
розподілу та ймовірність безвідмовної
роботи відповідно
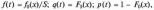 де
де
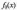 і
і
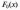 беруть за таблицями, наявними в довідниках.
Нижче наведено фрагмент такої таблиці:
беруть за таблицями, наявними в довідниках.
Нижче наведено фрагмент такої таблиці:
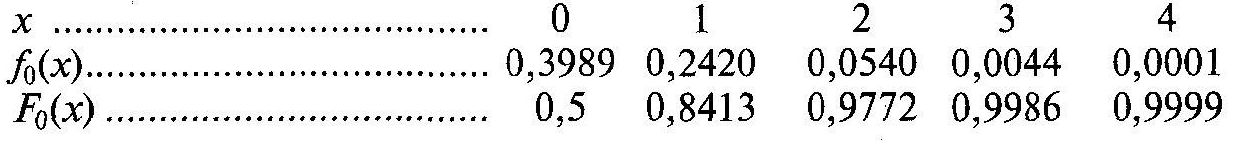
У
літературі з надійності часто замість
інтегральної функції розподілу
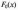 користуються функцією Лапласа
користуються функцією Лапласа
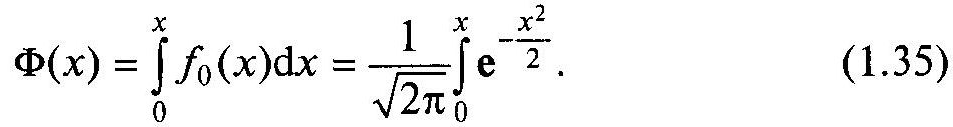
Очевидно, що
![]()
Імовірність відмови і ймовірність безвідмовної роботи, виражені через функції Лапласа, розрізняються межами інтегрування, мають такий вигляд:
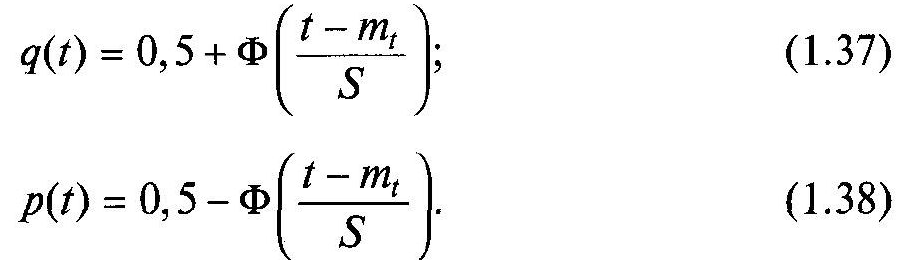
Порівнюючи
вироби з однаковим середнім напрацюванням
до відмови c різним середнім квадратичним
відхиленням
 потрібно підкреслити, що хоча при великих
потрібно підкреслити, що хоча при великих
 і є екземпляри з великою довговічністю,
але чим менше
і є екземпляри з великою довговічністю,
але чим менше
 тим багато кращі вироби.
тим багато кращі вироби.
Крім завдання оцінки ймовірності безвідмовної роботи за заданий час або задане напрацювання зустрічається зворотна задача визначення часу або напрацювання, відповідних заданій імовірності безвідмовної роботи. Значення цього напрацювання (часу) визначають за допомогою квантилів нормованого нормального розподілу
![]()
Значення квантилів даються в таблицях в залежності від необхідної ймовірності, зокрема від ймовірності безвідмовної роботи. Нижче як приклад наводиться фрагмент такої таблиці:
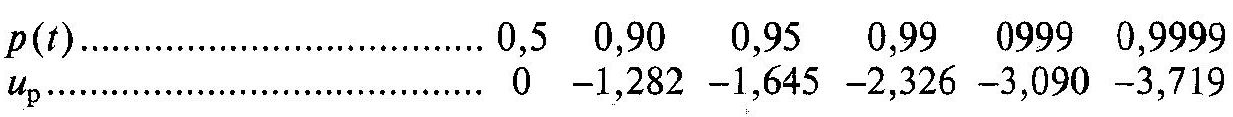
Операції
з нормальним розподілом простіші, ніж
з іншими, завдяки простим формулам і
наявними таблицями, тому ним часто
замінюють інші розподіли. При малих
коефіцієнтах варіації
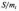 нормальний розподіл добре замінює
біномінальний, пуасонівський і
логарифмічно нормальний розподіли.
нормальний розподіл добре замінює
біномінальний, пуасонівський і
логарифмічно нормальний розподіли.
Розподіл
суми незалежних випадкових величин
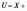
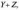 називається композицією розподілів,
при нормальному розподілі складових
також є нормальним розподілом. Математичне
сподівання і дисперсія композиції
відповідно:
називається композицією розподілів,
при нормальному розподілі складових
також є нормальним розподілом. Математичне
сподівання і дисперсія композиції
відповідно:
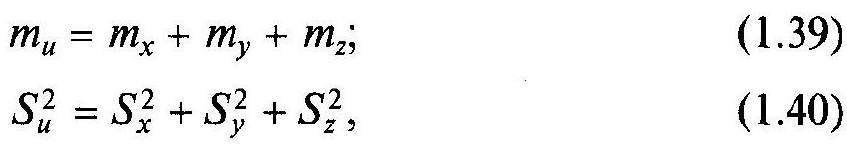
де
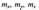 — математичні очікування випадкових
величин
— математичні очікування випадкових
величин
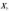
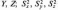 —
дисперсія
тих же величин.
—
дисперсія
тих же величин.
Приклад
1.2. Оцінити ймовірність
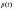 безвідмовної роботи протягом часу
безвідмовної роботи протягом часу
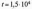 год зношуємого рухомого сполучення,
якщо ресурс по зносу підпорядковується
нормальному розподілу з параметрами
год зношуємого рухомого сполучення,
якщо ресурс по зносу підпорядковується
нормальному розподілу з параметрами
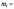
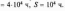
Рішення.
Знаходимо квантиль
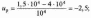 по табл. 1.1 визначаємо, що
по табл. 1.1 визначаємо, що
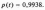
Приклад
1.3. Оцінити
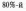 ресурс
ресурс
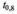 гусениці трактора, якщо відомо, що
довговічність гусениці обмежена по
зносу, ресурс підпорядковується
нормальному розподілу з параметрами
гусениці трактора, якщо відомо, що
довговічність гусениці обмежена по
зносу, ресурс підпорядковується
нормальному розподілу з параметрами
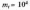 ч;
ч;
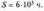
Рішення.
При
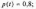
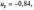 тоді ресурс складе, ч:
тоді ресурс складе, ч:
![]()
Усічений
нормальний розподіл виходить з нормального
при обмеженні інтервалу зміни випадкової
величини (рис. 1.8, б). Воно, зокрема, вносить
уточнення в розрахунки надійності в
порівнянні з нормальним розподілом при
великих значеннях коефіцієнта варіації
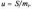
Функція щільності розподілу записується так само, як щільність нормального розподілу, але з коефіцієнтом пропорційності з:
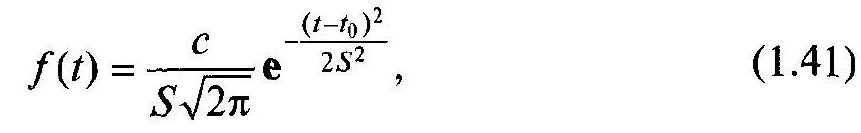
де
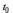 —
значення випадкової величини, відповідне
максимуму
—
значення випадкової величини, відповідне
максимуму
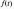 і називається модою.
і називається модою.
Коефіцієнт
 для розподілу, обмеженої межами зміни
для розподілу, обмеженої межами зміни
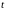 від
від
 до
до
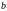 ,
визначається з умови
,
визначається з умови
![]()
де
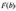 і
і
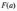 — значення функції нормального розподілу
для граничних значень
— значення функції нормального розподілу
для граничних значень
 Звідси
Звідси

Користуючись
функцією
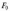 нормального розподілу нормованої та
центрованої випадкової величини,
запишемо:
нормального розподілу нормованої та
центрованої випадкової величини,
запишемо:
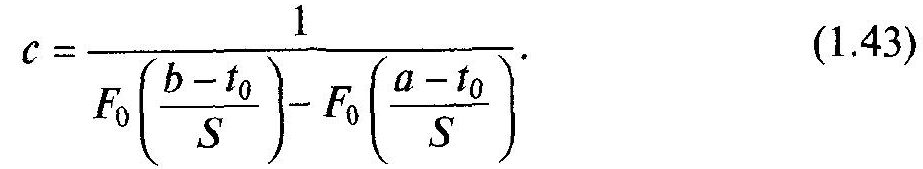
Основне
застосування усічений нормальний
розподіл має з параметрами
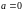 і
і
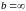 ,
відображає в задачах надійності
неможливість відмов при негативних
значеннях часу. При цьому
,
відображає в задачах надійності
неможливість відмов при негативних
значеннях часу. При цьому

Таблиця 1
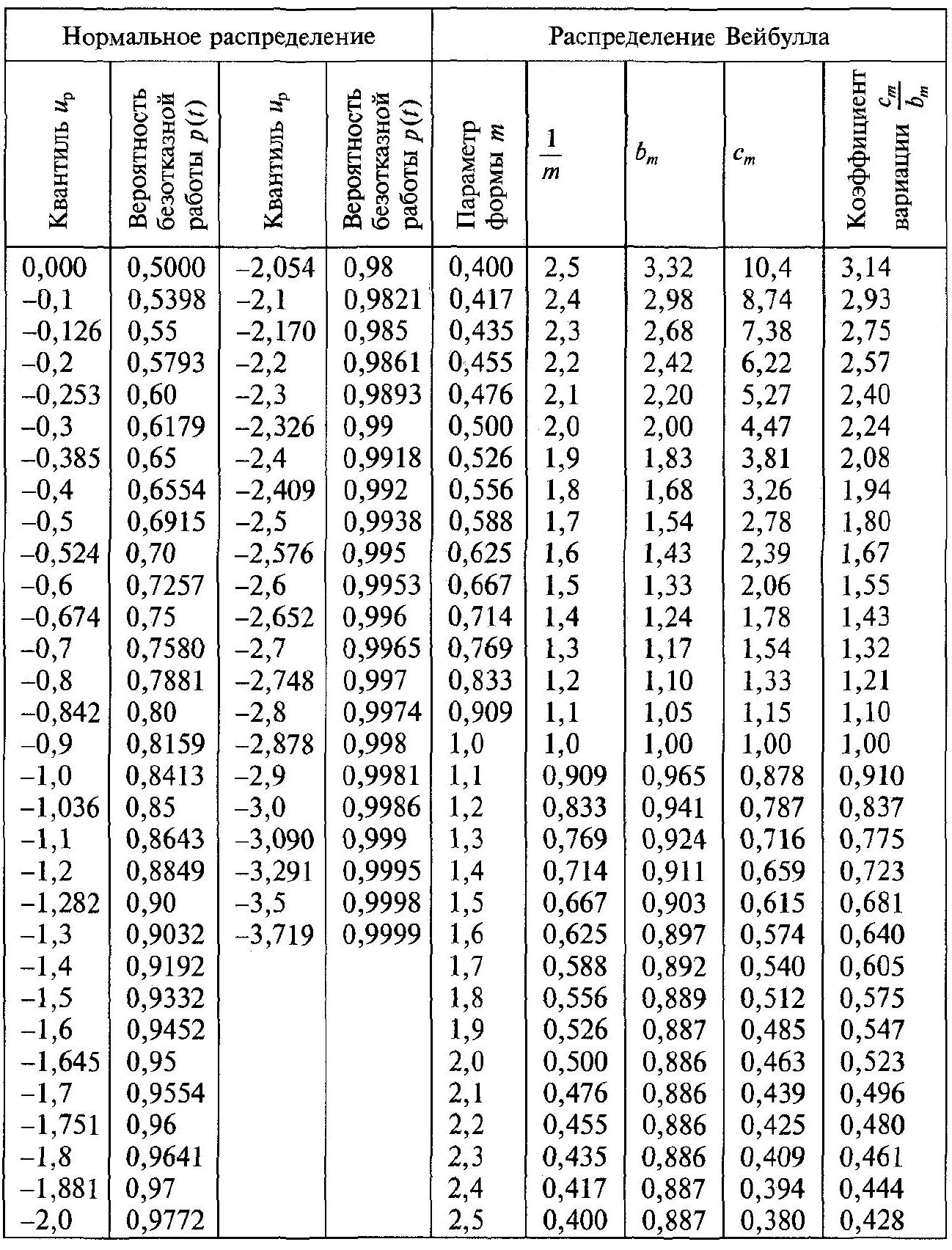
Примітки: 1. Під розуміється час або інші випадкові величини.
2.
Для логарифмічно нормального розподілу
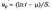
Значення
з можна вибрати залежно від
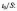
![]()
Таким
чином, при
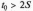 коефіцієнт
дуже близький до 1.
коефіцієнт
дуже близький до 1.
Ймовірність безвідмовної роботи
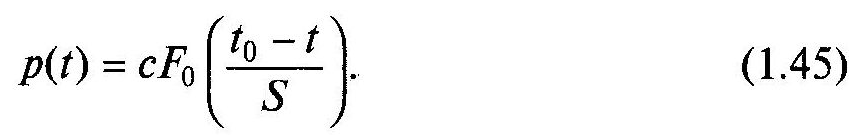
Середній ресурс
![]()
де
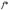 —
функція, яка визначається за табл. 1.1.
—
функція, яка визначається за табл. 1.1.
Прикладом усічених розподілів може бути розподіл параметра якості виробів після відбракування частини виробів по цьому параметру.
У логарифмічно нормальному розподілі логарифм випадкової величини розподіляється по нормальному закону. Як розподіл позитивних величин, воно дещо точніше, ніж нормальне, описує напрацювання до відмови деталей, зокрема, по втомі. Його успішно застосовують для опису напрацювання підшипників кочення, електронних ламп та інших виробів.
Логарифмічно нормальний розподіл зручний для випадкових величин, що представляють собою добуток значного числа випадкових вихідних величин, подібно тому як нормальний розподіл зручно для суми випадкових величин.
Щільність розподілу (рис. 1.10) описується залежністю
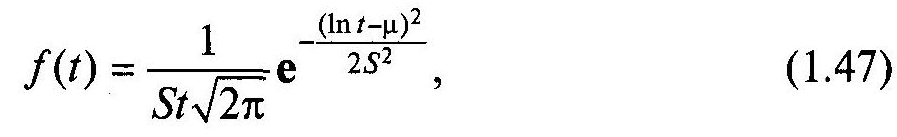
де
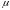 і
і
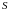 — параметри, які оцінюються за результатами
випробувань. Так, при випробуваннях
— параметри, які оцінюються за результатами
випробувань. Так, при випробуваннях
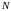 виробів до відмови
виробів до відмови
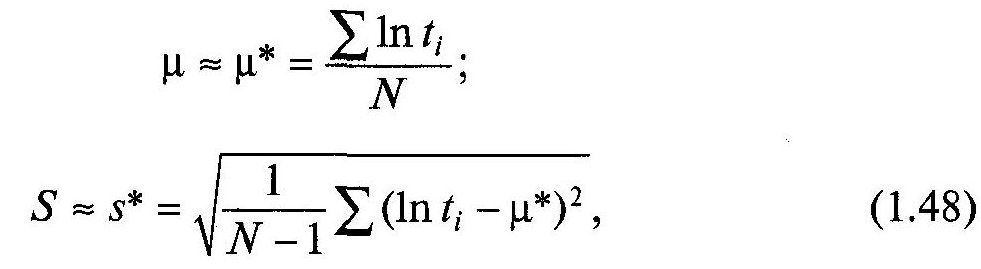
де
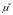 и
— оцінка параметрів
і
.
и
— оцінка параметрів
і
.
На рис. 1.10 час зазначено в тисячах годин. Для різних типів виробів конкретні значення часу можуть суттєво змінюватися. При цьому характерний вигляд графіків зберігається.
Ймовірність безвідмовної роботи можна визначити за таблицями для нормального розподілу (див. табл. 1.1) в залежності від

Рис. 1.10. Основні характеристики логарифмічного розподілу при різних параметрах:
— щільність
ймовірності
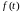 ;
;
б
— ймовірність безвідмовної роботи
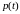 ;
;
в
— інтенсивність відмов
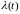 .
.
значення
квантилі
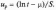 Інші параметри визначають за формулами.
Інші параметри визначають за формулами.
Математичне сподівання напрацювання до відмови:
![]()
Середнє квадратичне відхилення:
![]()
Коефіцієнт варіації:
![]()
При
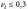 вважають
вважають
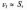 при цьому помилка складає менше 1%.
при цьому помилка складає менше 1%.
Часто застосовують запис залежностей для логарифмічно нормального розподілу в десяткових логарифмах. Відповідно щільність розподілу
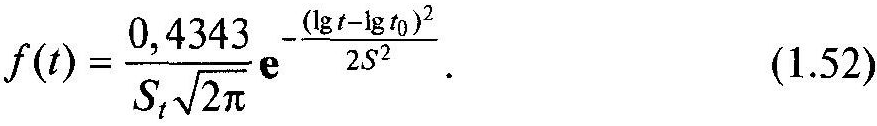
Оцінки
параметрів
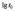 и
и
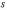 визначають за результатами випробувань:
визначають за результатами випробувань:
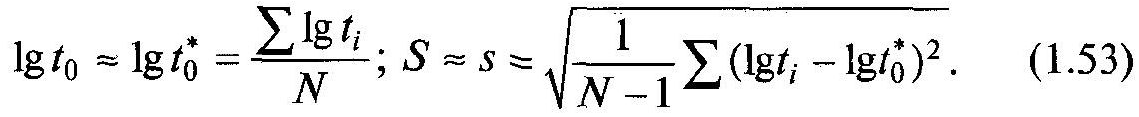
Математичне
сподівання
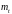 середнє квадратичне відхилення
середнє квадратичне відхилення
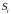 і коефіцієнт варіації
і коефіцієнт варіації
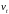 напрацювання до відмови відповідно
визначають за наступними формулами:
напрацювання до відмови відповідно
визначають за наступними формулами:
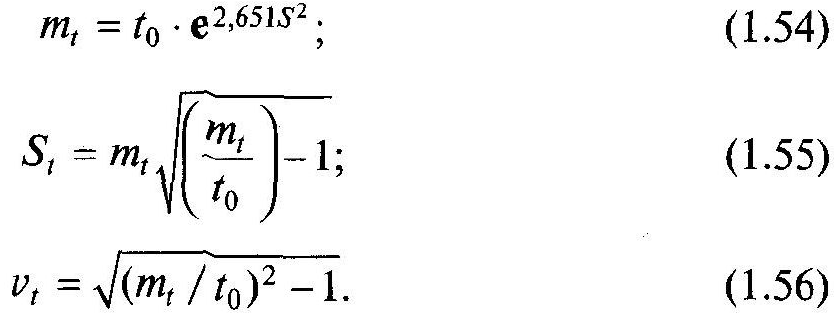
При
значеннях
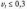 можна вважати
можна вважати
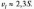
Для
ймовірностей безвідмовної роботи
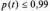 і при
і при
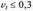 логарифмічно нормальний закон можна
замінювати нормальним законом з
параметрами
логарифмічно нормальний закон можна
замінювати нормальним законом з
параметрами
 і
і
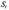 і щільністю
і щільністю
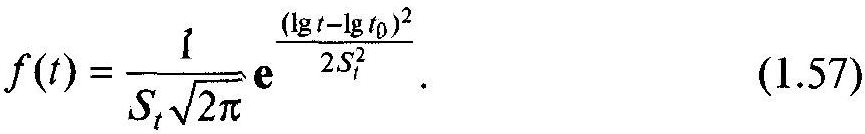
Ймовірність безвідмовної роботи можна знаходити за спеціальними таблицями для цього розподілу або таблицями для нормального розподілу.
Приклад
1.4, Оцінити ймовірність
відсутності втомних пошкоджень валу
протягом
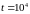 ч, якщо ресурс розподілений логарифмічно
нормально з параметрами
ч, якщо ресурс розподілений логарифмічно
нормально з параметрами
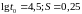 .
.
Рішення.
Ймовірність
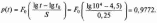
Розподіл Вейбулла є універсальним і охоплює широкий діапазон зміни ймовірностей. Поряд з логарифмічно нормальним розподілом він задовільно описує напрацювання деталей за втомними руйнуваннями, напрацювання до відмови підшипників, електронних ламп. Використовується для оцінки надійності деталей і вузлів машин, зокрема, автомобілів, підйомно-транспортних та інших машин. Застосовується також для оцінки надійності по приробочних відмов.
Розподіл характеризується наступною функцією ймовірності безвідмовної роботи (рис. 1.11):
![]()
Інтенсивність відмов:
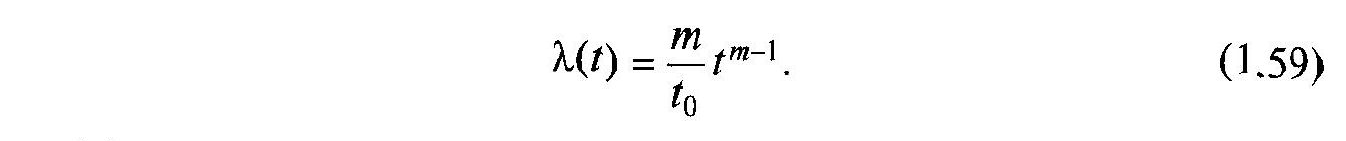
Щільність розподілу:
![]()
Розподіл
Вейбулла має також два параметри:
параметр форми
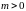 і параметр масштабу
і параметр масштабу
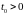 .
.
Математичне сподівання і середнє квадратичне відхилення відповідно:
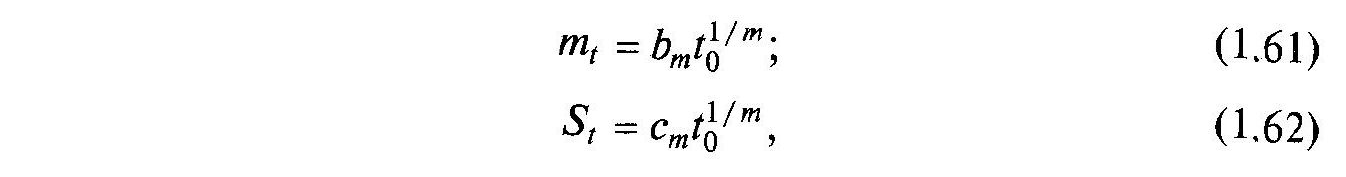
де
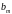 і
і
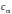 - коефіцієнти (див. табл. 1.1).
- коефіцієнти (див. табл. 1.1).
Якщо
протягом часу
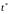 відмови не наступають, то формули для
характеристик надійності модифікуються.
Так, ймовірність безвідмовної роботи
відмови не наступають, то формули для
характеристик надійності модифікуються.
Так, ймовірність безвідмовної роботи
![]()
Можливості та універсальність розподілу Вейбулла очевидні з наступних пояснень (див. рис. 1.11):
при
![]() функції
функції
![]() і
і
![]() від напрацювання до відмови спадаючі;
від напрацювання до відмови спадаючі;
при
![]() розподіл перетворюється в експоненційний
розподіл перетворюється в експоненційний
![]() і
і
![]()
спадна функція;
спадна функція;
при
![]() функція
- одновершинна, функція
функція
- одновершинна, функція
![]() безперервно зростаюча при
безперервно зростаюча при
![]() з опуклістю вгору, а при
з опуклістю вгору, а при
![]()
З опуклістю вниз;
З опуклістю вниз;
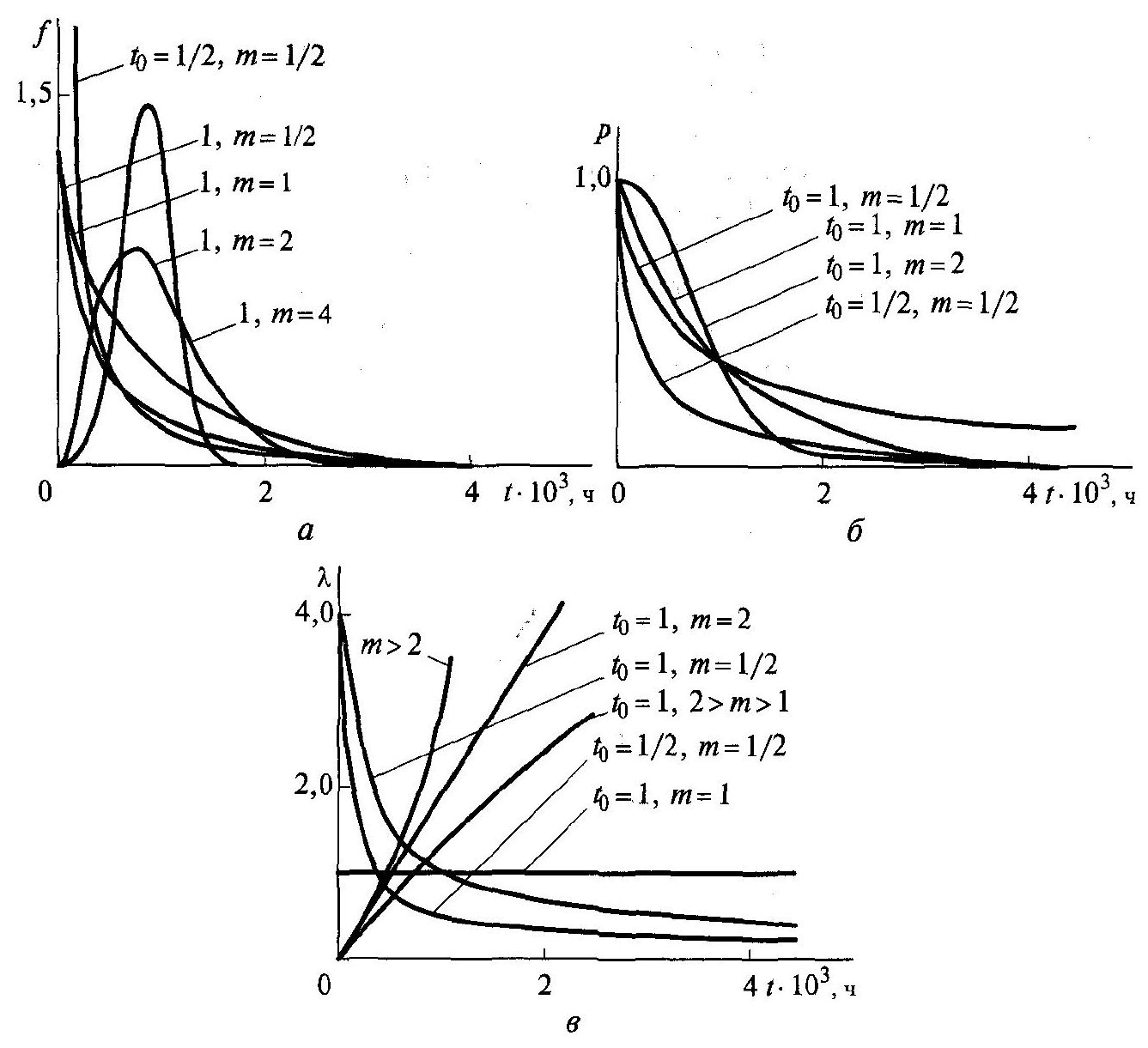
Рис.
1.11. Основні характеристики розподілу
Вейбулла за різних параметрах
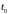 і
і
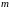 .
а
щільність вірогідності
.
а
щільність вірогідності
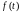 ;б
- ймовірність безвідмовної роботи
;в
- інтенсивності відмов
.
;б
- ймовірність безвідмовної роботи
;в
- інтенсивності відмов
.
при
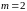 функція
є лінійною і розподіл Вейбулла
перетворюється на так званий розподіл
Релея;
функція
є лінійною і розподіл Вейбулла
перетворюється на так званий розподіл
Релея;
при
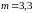 розподілі Вейбулла близький до
нормального.
розподілі Вейбулла близький до
нормального.
Графічна обробка результатів випробувань для розподілу Вейбулла проводиться в такій послідовності: логарифмують вираз для :
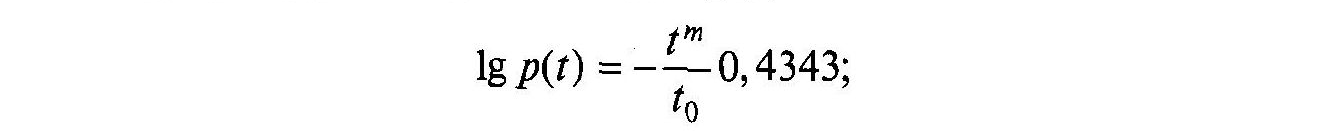
вводять
позначення
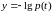 і логарифмують:
і логарифмують:
![]()
де
![]()
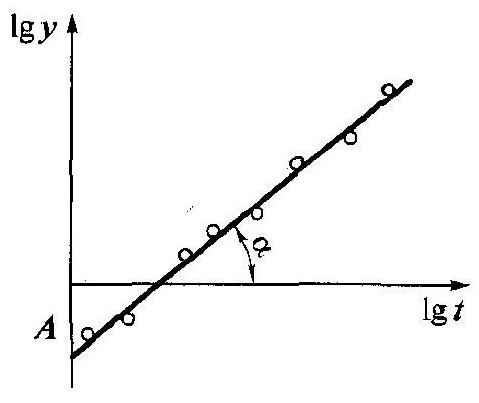
Рис. 1.12. Графічне визначення параметрів розподілу Вейбулла
відкладають
результати випробувань на графіку в
координатах
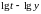 (рис. 1.12), проводять через отримані точки
пряму і отримують
(рис. 1.12), проводять через отримані точки
пряму і отримують
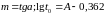 ,
де
кут нахилу прямої до осі абсцис;
,
де
кут нахилу прямої до осі абсцис;
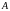 - відрізок, відтинають пряму на осі
ординат.
- відрізок, відтинають пряму на осі
ординат.
Надійність системи з послідовно з'єднаних однакових елементів, що підкоряються розподілу Вейбулла, також підпорядковуються розподілу Вейбулла.
Приклад 1.5.
Оцінити ймовірність безвідмовної роботи
роликопідшипників протягом
ч. години, якщо ресурс підшипників
описується розподілом Вейбулла з
параметрами
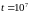 ч,
ч,
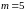
Рішення. Ймовірність