1.6 Надійність в період нормальної експлуатації
У період нормальної експлуатації поступові відмови ще не проявляються і надійність характеризується раптовими відмовами. Ці відмови викликаються несприятливим збігом багатьох обставин і тому мають постійну інтенсивність, яка не залежить від віку виробу:
де
— середнє напрацювання до відмови
(зазвичай у годинах).
Тоді виражається числом відмов на годину і, як правило, складає малий дріб.
Ймовірність безвідмовної роботи
підпорядковується експоненціальному закону розподілу часу безвідмовної роботи і однакова за будь-який однаковий проміжок часу в період нормальної експлуатації.
Експоненціальним законом розподілу можна апроксимувати час безвідмовної роботи широкого кола об'єктів (виробів): особливо відповідальних машин, експлуатованих в період після закінчення припрацювання і до істотного вияву поступових відмов; елементів радіоелектронної апаратури; машин з послідовною заміною деталей, які відмовили; машин разом з електро- та гідро- обладнання і системами управління та ін; складних об'єктів, що складаються з багатьох елементів (при цьому час безвідмовної роботи кожного може не бути розподіллено за експоненціальним законом; потрібно тільки, щоб відмови одного елемента, який не підкоряється цьому закону, не домінували над іншими).
Суттєва перевага експоненціального розподілу - його простота: вона має тільки один параметр.
У
більшості випадків
і формула для ймовірності безвідмовної
роботи спрощується в результаті
розкладання в ряд і відкидання малих
членів:
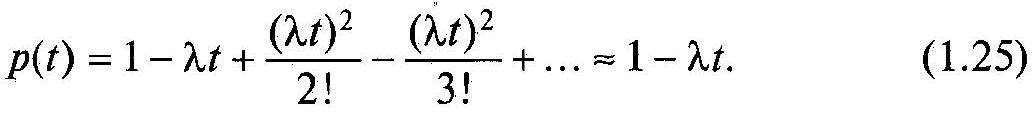
Щільність розподілу (в загальному випадку)
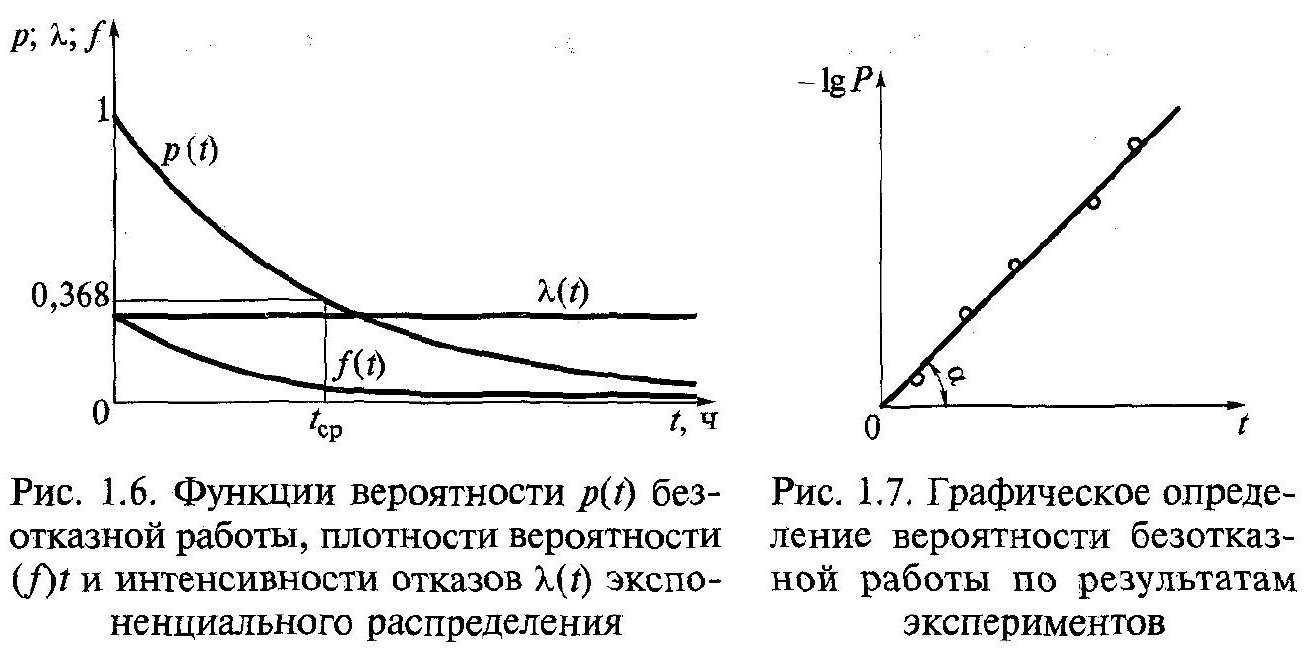
Нижче
наведені значення імовірності безвідмовної
роботи залежно від
див. формулу (1.24) (рис. 1.6):
Оскільки
при
ймовірність
, то
відмов виникає за час
та тільки
пізніше. З наведених значень випливає,
що для забезпечення необхідної ймовірності
безвідмовної роботи 0,9 або 0,99 можна
використовувати лише малу частку
середнього терміну служби (відповідно
0,1 і 0,01).
Якщо
робота виробу відбувається в різних
режимах, а отже, і інтенсивностях відмов
(за час
)
і
(за час
),
то
Ця залежність випливає з теореми множення ймовірностей.
Для
визначення на підставі дослідів
інтенсивності відмов
спочатку оцінюють середні напрацювання
до відмови
де
— загальне число спостережень. Тоді
.
Можна
також скористатися графічним способом
(рис. 1.7) — нанести експериментальні
точки в координатах
і
.
Знак
вибирають тому, що
і, отже,
— негативна величина. Тоді, логарифмуючи
вираз для ймовірності безвідмовної
роботи:
, отримуємо тангенс кута прямої, проведеної
через експериментальні точки
звідки
При використанні графічного способу немає необхідності доводити до кінця випробування всіх зразків.
Для системи
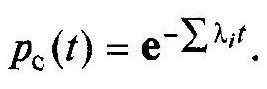
Якщо
то
Таким чином, ймовірність безвідмовної роботи системи, що складається з елементів з імовірністю безвідмовної роботи, що підкоряються експоненціальному закону, також підпорядковується експоненціальному закону. При цьому інтенсивності відмов окремих елементів перемножуються.
Використовуючи
експонентний закон розподілу, нескладно
визначити середнє число виробів
,
які вийдуть з ладу до заданого моменту
часу, і середнє число виробів
які залишаться працездатними. При
Приклад
1.1. Оцінити ймовірність
відсутності раптових відмов механізму
протягом
, якщо інтенсивність відмов становить
.
Рішення.
Оскільки
,
то скористаємося наближеною залежністю
