1.4 Оцінка параметрів надійності

Істотне розсіювання основних параметрів надійності зумовлює необхідність розглядати її в імовірнісному аспекті.

Як було показано раніше на прикладі характеристики розподілів, параметри надійності використовуються в статистичному трактуванні для оцінки стану і в ймовірнісному трактуванні  для прогнозування. Перші виражаються в дискретних числах, їх в теорії ймовірностей і математичній теорії надійності називають оцінками. При достатньо великій кількості випробувань вони приймаються за істинні характеристики надійності.

Розглянемо проведені для оцінки надійності випробування або експлуатація значного числа елементів протягом часу (або напрацювання в інших одиницях). Нехай до кінця випробування або терміну експлуатації залишиться працездатних (які ще не відмовили) елементів і , які відмовили.

Тоді відносне число відмов

Якщо випробування проводиться як вибіркове, то можна розглядати як статистичну оцінку ймовірності відмови або, якщо досить велике, як ймовірність відмови.

Надалі у випадках, коли необхідно підкреслювати відмінність оцінки ймовірності від істинного значення ймовірності, оцінка буде додатково позначатися знаком , зокрема .

Ймовірність безвідмовної роботи оцінюється відносним числом працездатних елементів

Оскільки безвідмовна робота і відмова  взаємно протилежні події, то сума їх ймовірностей дорівнює 1:

Це ж випливає з наведених раніше залежностей:

Розподіл відмов в часі характеризується функцією щільності розподілу напрацювання до відмови. У статистичній трактуванні

в ймовірнісному трактуванні

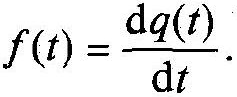
Тут та — прирощення числа об'єктів які відмовили і відповідно ймовірності відмов за час

Ймовірності відмов та безвідмовної роботи в функції щільності виражаються наступними залежностями:

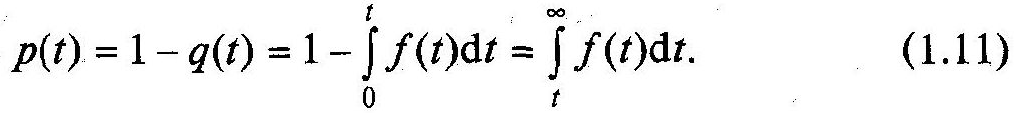
Інтенсивність відмов на відміну від щільності розподілу відноситься до числа об'єктів , які залишилися працездатними, а не до загального числа об'єктів. Відповідно до статистичного трактування

і в ймовірнісному трактуванні, враховуючи, що

Отримаємо вираз для ймовірності безвідмовної роботи залежно від інтенсивності відмов. Для цього в вираз (1.13) підставимо , розділимо змінні і проінтегруємо:

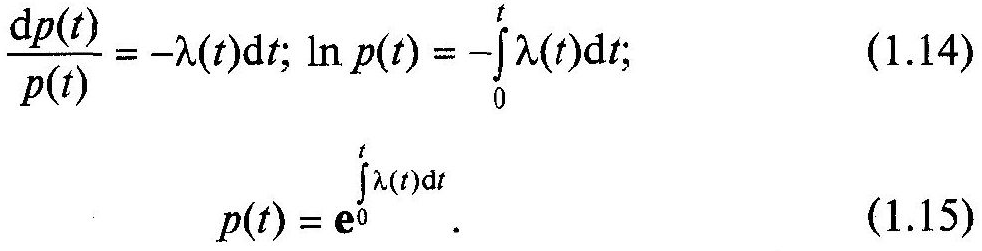
Співвідношення (1.15) є одним з основних рівнянь теорії надійності.

До числа найважливіших загальних залежностей надійності відносяться залежності надійності систем від надійності елементів.

Розглянемо надійність яка э найбільш характерною для машинобудування найпростішої розрахункової моделі системи з послідовно з'єднаних елементів (рис. 1.2), у якій відмова кожного елемента викликає відмову системи, а відмови елементів приймаються незалежними.

Використовуємо відому теорему множення ймовірностей, згідно з якою ймовірність добутку, тобто спільного прояви незалежних подій, дорівнює добутку ймовірностей цих подій.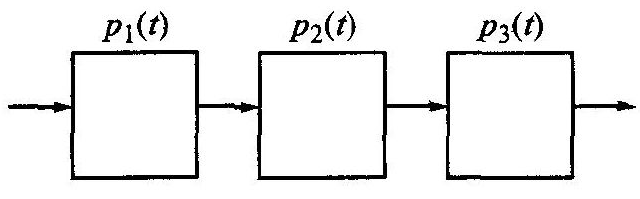

Рис. 1.2. Структурна схема надійності послідовної системи

Отже, ймовірність безвідмовної роботи системи дорівнює добутку ймовірностей безвідмовної роботи окремих елементів:

Виходячи з того, що то ,надійність складних систем виходить низькою. Наприклад, якщо система складається з 10 елементів з імовірністю безвідмовної роботи 0,9 (як в підшипниках кочення), то загальна ймовірність становить .

Зазвичай ймовірність безвідмовної роботи елементів досить висока, тому, виразивши через ймовірності відмов і користуючись теорією наближених обчислень, отримаємо

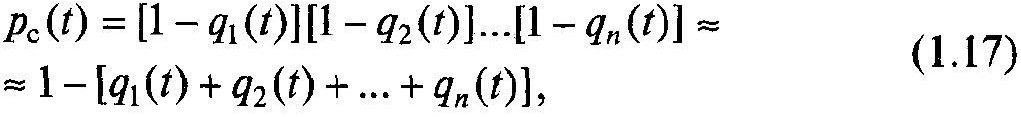
так як добутками двох малих величин можна знехтувати. При отримуємо . Нехай в системі з шести однакових послідовних елементів , тоді та . Ймовірність безвідмовної роботи потрібно вміти визначати для будь-якого проміжку часу. По теоремі множення ймовірностей

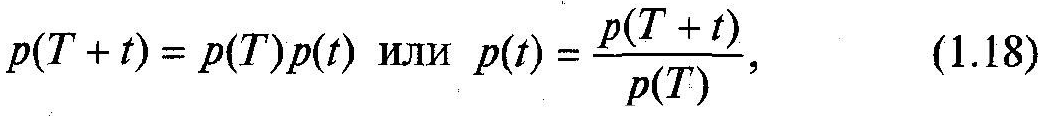
де и — ймовірності безвідмовної роботи за час і відповідно; — умовна ймовірність безвідмовної роботи за час (термін «умовна» тут введено, оскільки передбачається, що вироби не мали відмови до початку інтервалу часу або напрацювання).