1.3 Випадкові величини та їх характеристики

Раптові відмови визначаються випадковими несприятливими поєднаннями кількох факторів. Випадковість пов'язана з тим, що причини події залишаються для нас прихованими. Розсіювання ресурсів за критерієм втоми (оцінювана ставленням найбільшого ресурсу до найменшого) для підшипників досягає 40, для зубчатих передач 10 ... 15. Розсіювання ресурсів по зносу також досить значне. Істотні розсіювання мають діючі навантаження, механічні характеристики матеріалів і деталей, зазори і натяг. Тому в розрахунках надійності багато параметрів, повинні розглядатися випадковими величинами, тобто такими, які можуть прийняти те чи інше значення, невідоме заздалегідь. Вони можуть бути безперервного або перервного (дискретного) типу.

Для кожного числа 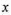в діапазоні зміни випадкової величини 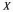існує певна ймовірність , що 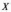не більша  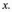Ця залежність 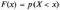називається функцією розподілу або функцією ймовірності випадкової величини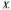

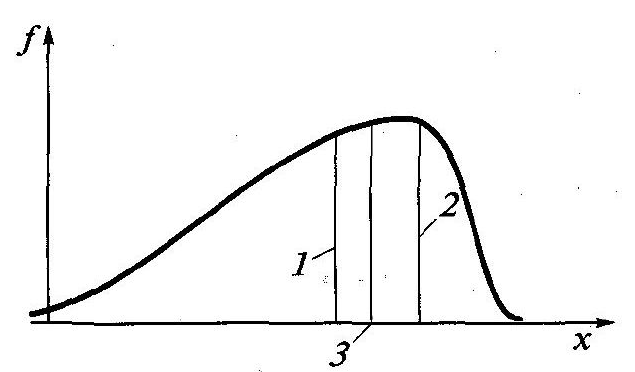
Рис. 1.1. Щільність ймовірності та числові характеристики центру групування випадкової величини: 1 - медіана; 2 - мода; 3 - математичне сподівання

Функція неубутною функцією (монотонно зростаючою для безперервних процесів і східчасто зростаючою для дискретних процесів). В межах зміни випадкової величини 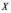вона змінюється від 0 до 1.

Похідна від функції розподілу за поточної змінної 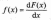називається щільністю розподілу. Вона характеризує частотою повторень даного значення випадкової величини. У завданнях надійності її широко використовують в якості щільності ймовірності.

У ряду випадків досить характеризувати розподіл випадкової величини деякими випадковими величинами: (рис. 1.1) математичним очікуванням (середнім значенням), модою і медіаною, що характеризують положення центрів групування випадкових величин на числовій осі, дисперсією, середнім квадратичним відхиленням, коефіцієнтом варіації, характеризує розсіювання випадкової величини.

Характеристики розподілів використовуються в статистичному трактуванні (для обробки результатів спостережень) і в ймовірнісному трактуванні (для прогнозування надійності).

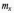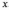Математичне сподівання (середнє значення) — основна і найпростіша характеристика випадкової величини . Значення математичного очікування, яке визначається за результатами спостережень як для дискретних, так і для безперервних величин, називають оцінкою математичного очікування або оцінкою середнього значення:

або

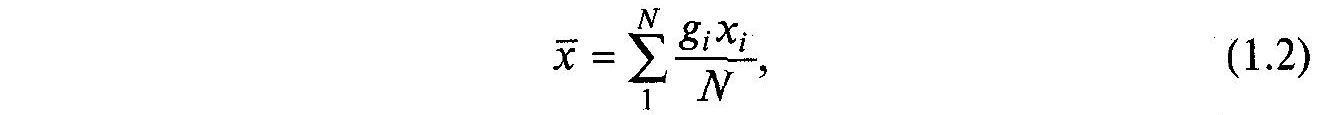
де — загальне число спостережень;

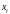— значення випадкової величини;

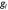— число однакових значень

Риска над позначенням випадкової величини означає середнє значення.

В формулі (1.1) сумують всі членів, а в формулі (1.2) — число членів з різними значеннями . При досить великому числі спостережень (випробувань) вважають, що

В імовірнісних задачах математичне очікування визначають залежно від щільності розподілу 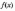(для безперервних величин) або ймовірності 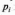появи значень (для дискрет­них величин):

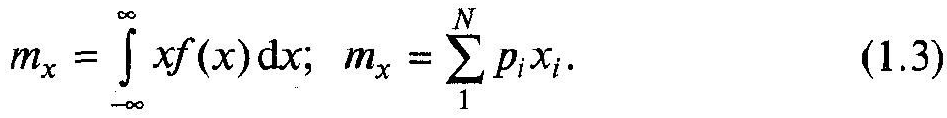
Дисперсія випадкової величини  математичне сподівання квадрата відхилення цієї величини від її математичного очікування.

Оцінка дисперсії випадкової величини  середнє значення квадрата різниці між значеннями випадкової величини і її середнім значенням:

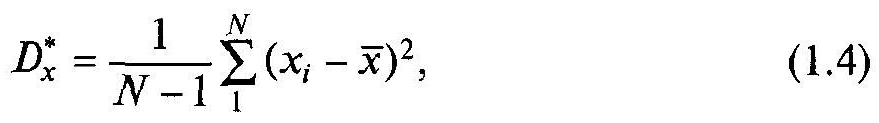
або

Слово «дисперсія» означає розсіювання і характеризує розкид випадкової величини.

Для непереривних випадкових величин

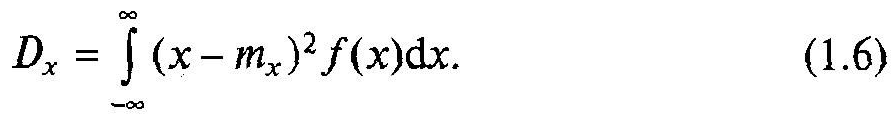
Для дискретних випадкових величин

Дисперсія має розмірність квадрата випадкової величини. Оскільки зручніше користуватися характеристикою розсіювання, що має ту ж розмірність, що і випадкова величина, то була введена характеристика  середнє квадратичне відхилення, яке представляє собою корінь квадратний з дисперсії,

Для оцінки розсіювання за допомогою безрозмірної (відносної) величини використовують коефіцієнт варіації, рівний відношенню середнього квадратичного відхилення до математичного очікування:

Дисперсія і середнє квадратичне відхилення є набагато більш репрезентативними характеристиками розсіювання, наприклад, середнє арифметичне абсолютних значень відхилень.

Квантиль  це середнє значення випадкової величини, відповідне заданній ймовірності. Квантиль, відповідний ймовірності 0,5, називається медіаною. Медіана характеризує розташування центру групування випадкової величини. Площа під графіком функції щільності розподілу ділиться медіаною навпіл.

Для характеристики розсіювання випадкової величини використовують також імовірнісне відхилення, рівне половині різниці квантилів та , тобто значень випадкової величини, відповідне ймовірностям 0,75 і 0,25.

Мода випадкової величини  найбільш ймовірне значення або, інакше, те її значення, при якому щільність ймовірності максимальна.

Аналогічно з попередніми характеристиками трансформуються терміни мода і медіана у статистичній трактуванні. Для симетричного модального (тобто що має один максимум) розподілу математичне сподівання, мода і медіана збігаються.