4.3. Надійність послідовних систем при нормальному розподілі навантаження по однотипним підсистемам

Якщо розсіювання навантаження по однотипним підсистемам пренебрежимо мало, а несучі здібності елементів незалежні один від одного, то відмови елементів статистично незалежні і тому ймовірність безвідмовної роботи послідовної системи з несучою здатністю при навантаженні дорівнює добутку ймовірностей безвідмовної роботи елементів:

де — ймовірність безвідмовної роботи -го елемента при навантаженні ; — число елементів у системі; — функція розподілу несучої здатності -го елемента при значенні випадкової величини

У більшості випадків навантаження на конкретні системи має істотне розсіювання при застосуванні систем, наприклад одні й ті ж універсальні машини (верстати, автомобілі та ін) можуть експлуатуватися в різних умовах. При розсіянні навантаження по системам оцінку ймовірності безвідмовної роботи системи в загальному випадку слід знаходити за формулою повної ймовірності, розбивши діапазон розсіювання навантаження на інтервали визначивши для кожного інтервалу навантаження добуток імовірності безвідмовної роботи -го елемента при фіксованій навантаженні на ймовірність цього навантаження а потім, підсумувавши ці твори по всім інтервалам, інтегрування,

або, переходячи до

де — щільність розподілу навантаження; — функція розподілу несучої здатності і-го елемента при значенні несучої здатності

Розрахунки за формулою (4.14) у загальному випадку трудомісткі, так як припускають чисельне інтегрування, тому при великому можливі тільки на ЕОМ. Щоб не обчислювати за формулою (4.14), на практиці часто оцінюють імовірність безвідмовної роботи систем при навантаженні максимальної з можливих. Приймають, зокрема, , де — математичне сподівання навантаження; — її коефіцієнт варіації. Це значення відповідає найбільшому значенню нормально розподіленої випадкової величини на інтервалі, рівному шести середнім квадратичним відхиленням навантаження. Такий метод оцінки надійності суттєво занижує розрахунковий показник надійності системи.

Існує досить точний метод спрощеної оцінки надійності послідовної системи для випадку нормального розподілу навантаження по системам. Ідея методу полягає в апроксимації закону розподілу несучої здатності системи нормальним розподілом так, щоб нормальний закон був близький істинному в діапазоні знижених значень несучої здатності системи, так як саме ці значення визначають величину показника надійності системи.

Порівняльні розрахунки на ЕОМ за формулою (4.14) (точне рішення) і за наведеним далі спрощеним методом показали, що точність спрощеного методу достатня для інженерних розрахунків надійності систем, у яких коефіцієнт варіації несучої здатності не перевищує 0,1 ... 0,15, а число елементів системи не більше 10 ... 15. Суть спрощеного методу полягає в наступному.

1. Задаються двома значеннями і фіксованих навантажень.

За формулою (4.13) проводять розрахунок ймовірностей безвідмовної роботи системи при цих навантаженнях. Навантаження підбирають з таким розрахунком, щоб при оцінці надійності системи ймовірність безвідмовної роботи системи вийшла в межах = 0,45...0,60 и = 0,95...0,99, тобто охоплювали б цікавить інтервал. Попередньо орієнтовні значення навантажень приймають близькими до значень

2 . В таблиці 4.1 знаходять квантилі нормального розподілення U_pА та U_pВ відповідні знайденим ймовірностям.

3. Апрксимують закон розподілу несучої властивості системи нормальним розподіленням з параметрами математичного очікування m_R і коефіцієнтом варіації v_R. Хай S_R – середнє квадратичне відхиленняапроксимуючого розподілу, тоді

За цими виразами находять

Таблиця 4.1

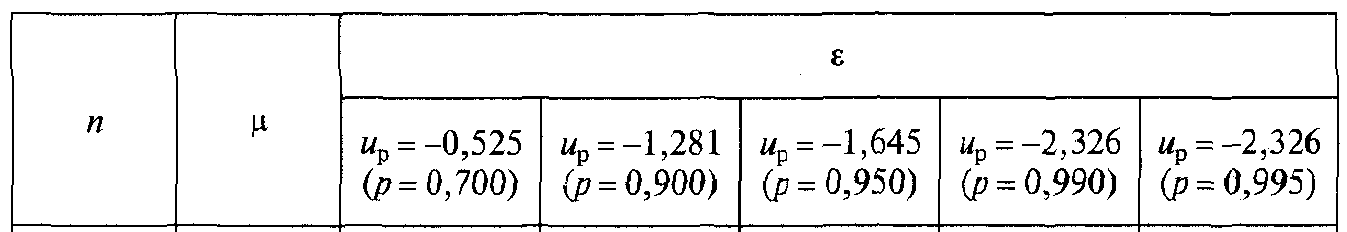
]	0,000	1,000	1,000	1,000	1,000	1,000
2	0,545	0,830	0,848	0,857	0,873	0,878
5	1,129	0,684	0,707	0,723	0,752	0,761
10	1,499	0,594	0,632	0,650	0,684	0,684
15	1,694	0,558	0,596	0,642	0,652	0,662
20	1,824	0,533	0,573	0,593	0,630	0,643
30	1,998	0,505	0,544	0,565	0,603	0,618
40	2,116	0,484	0,527	0,550	0,586	0,599
50	2,204	0,469	0,513	0,533	0,574	0,588
60	2,274	0,463	0,503	0,526	0,560	0,581
80	2,371	0,450	0,498	0,516	0,558	0,570
100	2,462	0,436	0,474	0,503	0,541	0,558
150	2,604	0,419	0,457	0,484	0,523	0,538
200	2,701	0,408	0,452	0,474	0,511	0,520
300	2,833	0,394	0,434	0,454	0,493	0,515
400	2,923	0,380	0,427	0,448	0,489	0,507
500	2,9923	0,377	0,420	0,436	0,485	0,496
1000	3,20	0,36	0,40	0,42	0,46	0,47
2000	3,39	0,35	0,38	0,40	0,43	0,44
5000	3,64	0,33	0,36	0,38	0,41	0,42
10000	3,81	0,32	0,35	0,36	0,40	0,41
20000	3,99	0,30	0,33	0,35	0,37	0,38
50000	4,21	0,27	0,32	0,33	0,36	0,37
100000	4,35	0,27	0,32	0,32	0,33	0,34

де — умовний запас міцності за середнім значенням несучої здатності і навантаження,

Використовування зазначеного методу розглянемо на прикладах.

Приклад 4.2. Оцінити ймовірність безвідмовної роботи одноступінчатого редуктора, якщо: умовні запаси міцності за середнім значенням несучої здатності і навантаження складають: для зубчастої передачі для підшипників вхідного вала для підшипників вихідного вала вихідного та вхідного валів Це відповідає математичним очікуванням несучої здатності елементів Часто в редукторах значення і і відповідно і бувають більше зазначених. Визнач, що несучі здібності передачі, підшипників та валів нормально розподілені з однаковими коефіцієнтами варіації а навантаження по редукторів розподілена також нормально з коефіцієнтом варіації

_{Рішення.} задаємося навантаженнями і Приймаємо

= припускаючи, що ці значення близькі до необхідним значенням

ймовірностей безвідмовної роботи систем при фіксованих навантаженнях и

Обчислюємо квантилі нормального розподілу всіх елементів, що відповідають їх можливостям безвідмовної роботи при навантаженнях і

Аналогічно

За квантиллю з табл. 4.1 знаходимо ймовірності безвідмовної роботи елементів:

• при навантаженні

• при навантаженні

Ймовірності безвідмовної роботи редуктора и

при фіксованих навантаженнях і оцінюємо за формулою (4.1) як добуток ймовірностей безвідмовної роботи елементів. Отримуємо

Із зіставлення цих значень з діапазонами допустимих значень, наведеними раніше, слід, що ймовірності знаходяться всередині цих діапазонів. Тому змінювати значення і не будемо.

За формулами (4.15), (4.16) обчислюємо математичне сподівання і коефіцієнт варіації v_R несучої здатності редуктора:

де і — квантилі нормального розподілу, відповідні ймовірностям и

За формулою (4.17) розраховуємо квантиль нормального розподілу, відповідну ймовірності безвідмовної роботи редуктора:

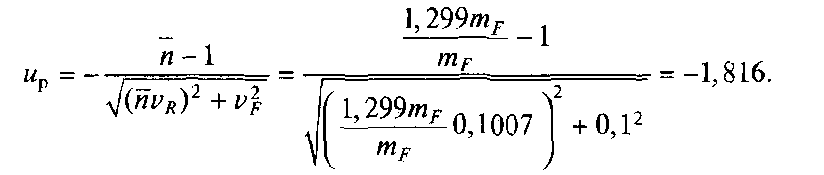
За табл. 4.1 знаходимо шукану ймовірність, відповідну отриманої квантилі:

Приклад 4.3. За вихідними даними прикладу 4.2 знайти ймовірність безвідмовної роботи редуктора по максимальному навантаженні відповідно з методикою, яку застосовували раніше для практичних розрахунків. Приймаємо максимальне навантаження

Рішення. Обчислюємо при цьому навантаженні квантилі нормального розподілу ймовірностей безвідмовної роботи елементів:

За табл. 4.1 знаходимо відповідні квантиль імовірності:

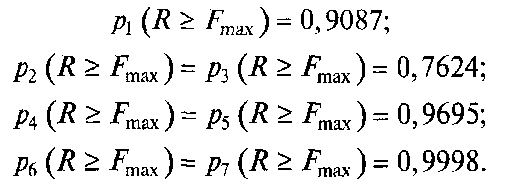
Ймовірність безвідмовної роботи редуктора при навантаженні обчислюємо за формулою (4.13). отримаємо

Із зіставлення результатів вирішення двох прикладів випливає, що перше рішення дає оцінку надійності значно ближчу до дійсної і більш високу, ніж у другому прикладі. Дійсне значення ймовірності, розраховане на ЕОМ за формулою (4.14), одно 0,9774.