4.2. Надійність систем з послідовно і паралельно з'єднаних елементів

Складний технічний пристрій або система складається з декількох окремих частин або комбінації різних груп однотипних елементів.

При розрахунку надійності будь-якого технічного пристрою або системи потрібно також враховувати тип з'єднання різних частин або елементів. Так, якщо припустити відмови частин пристрою або елементів системи незалежними, то на підставі теорем теорії ймовірностей можна представити наступні рівняння для розрахунку надійності, наприклад, комбінації з двох частин або елементів.

1. Якщо — надійність одного елемента системи, а — надійність іншого, то ймовірність того, що обидва елементи, з'єднані послідовно, будуть працювати безвідмовно протягом заданого проміжку часу ,

2. Імовірність того, що один або обидва елементи системи відмовлять,

3. Імовірність того, що будуть працювати один або два елементи системи,

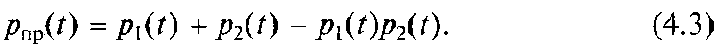
4. Імовірність того, що обидва елементи відмовлять,

В формулах (4.1)—(4.4) — надійність послідовно з'єднаних елементів системи; — ймовірність відмови цієї системи. У такій системі згідно рівняння (4.1) відмова будь-якого елемента приводить до відмови системи; и — відповідно надійність і вірогідність відмови паралельного з'єднання елементів або системи з постійним навантаженим резервом.

У цьому випадку згідно рівняння (4.3) при відмові одного елемента існує інший, який виконує необхідну функцію і, отже, така паралельна система з двох елементів не відмовляє в роботі, якщо відмовив один елемент.

Рівняння (4.1) - (4.4) справедливі як для експоненціального, так і неекспоненціального розподілу відмов елементів у системі або складових частин у пристрої.

При послідовному з'єднанні п елементів або блоків в системі, а також складових частин у пристрої надійність системи або пристрої у відповідності з рівнянням (4.1) складе

де — надійність -го елемента або блоку в послідовному з'єднанні. тут надійність може бути як експоненціальною, так і не експоненційної функцією часу.

Імовірність відмови системи або пристрою, що складаються відповідно з послідовного з'єднання елементів або частин, згідно з рівнянням (4.2)

Якщо величини надійності окремих елементів у системі або складових частин якого-небудь пристрою змінюються в часі за експоненціальним законом

то рівняння (4.5), з урахуванням рівняння (4.7), набуде вигляду

де — середні постійні величини інтенсивностей відмов окремих елементів або складових частин пристрою в частках одиниці на 1 год роботи; — час роботи елементу або частини пристрою, год.

При паралельному з'єднанні одночасно працюючих елементів або блоків в системі вірогідність відмови системи у відповідності з рівнянням (4.4)

де — ймовірність відмови і-го елемента або блоку в паралельному з'єднанні,

Тоді надійність системи з п паралельно працюючих у ній елементів або блоків виражається наступним чином:

Якщо паралельно працюючі елементи в системі однакові, то рівняння (4.9) і (4.10) приймають наступний вид:

Для ілюстрації застосування, наприклад, рівнянь (4.5), (4.6) і (4.7) далі наводиться числовий приклад визначення конструкційної надійності електричної машини постійного струму.

Приклад 4.1. Визначити конструкційну надійність машини постійного струму типу ПН-100 для трьох інтервалів часу її роботи: = 1000, 3 000 і 5000 год, з наступними середніми статистичними даними про інтенсивність відмов основних її частин у частках одиниці на 1 год роботи: магнітна система з обмоткою збудження — ; обмотка якоря — ; підшипники ковзання — ; колектор — і щітковий пристрій —

Рішення. Згідно з рівнянням (4.8) визначаємо середню результуючу інтенсивність відмов всіх частин машини, :

Середнє напрацювання до першої відмови машини, год:

Ймовірність безвідмовної роботи, або конструкційна надійність, розглянутої машини по рівнянню (4.8) для трьох інтервалів часу роботи складе:

Як випливає з отриманих даних, конструкційна надійність розглянутої машини постійного струму характеризується тим, що у відповідності з рівнянням (4.6) на кожні 1000 машин ймовірність виходу з ладу протягом зазначених трьох проміжків часу роботи становить: у першому випадку - 5 машин, або 0, 5%, у другому - 12 машин, або 1,2%; та в третьому - 25 машин, або 2,5%.