
- •Вища професійна освіта в. Ю. Шишмарев надійність технічних систем
- •Розділ 1: основні поняття теорії надійності
- •1.1 Основні терміни та визначення
- •1.2 Показники надійності
- •1.3 Випадкові величини та їх характеристики
- •1.4 Оцінка параметрів надійності
- •1.5 Різні періоди роботи технічних пристроїв
- •1.6 Надійність в період нормальної експлуатації
- •1.7 Надійність в період поступових відмов, що виникають через зношування і старіння
- •1.8 Спільна дія раптових і поступових відмов
- •1.9 Особливості надійності відновлюваних виробів
- •Глава 2
- •2 Надійність неремонтуємих об’єктів
- •2.1 Показники надійності неремонтуємих об’єктів
- •2.2. Теоретичні розподіли наробітку до відмови
- •Глава 3
- •3.1. Показники надійності ремонтованих об'єктів, не відновлюваних в процесі застосування
- •3.2. Показники надійності ремонтованих об'єктів, відновлюваних в процесі застосування
- •3.3. Ремонтопридатність і готовність технічних пристроїв
- •3.4. Методи випробування на надійність і статистичної обробки дослідних даних
- •Глава 4
- •4.1. Загальні відомості
- •4.2. Надійність систем з послідовно і паралельно з'єднаних елементів
- •4.3. Надійність послідовних систем при нормальному розподілі навантаження по однотипним підсистемам
- •4.5. Надійність систем з резервуванням
3.2. Показники надійності ремонтованих об'єктів, відновлюваних в процесі застосування
Показники надійності таких об'єктів обчислюються лише в календарному часі.
Відновлювані в процесі застосування ремонтовані об'єкти можна розділити на дві групи.
До першої групи належать об'єкти, для яких протягом заданого часу роботи допускаються відмови і викликані ними короткочасні перерви в роботі. Для об'єктів цієї групи велике значення має властивість готовності - здатності перебувати в процесі експлуатації максимальний час в працездатному і готовому до застосування стані.
До другої групи належать об'єкти, відмови яких протягом заданного часу неприпустимі. Якщо в цих об'єктах (системах) є надлишкові елементи, то при відмовах деяких з них об'єкт залишається працездатним і можна проводити ремонт елементів, які відмовили під час виконання завдання.
Один і той самий об'єкт може бути віднесений до різних груп в залежності від режиму його застосування.
Розглянемо процес експлуатації об'єктів першої групи (рис. 3.2). Після відмови (відзначений хрестиком) об'єкт деякий час перебуває в непрацездатному стані, тобто ремонтується.
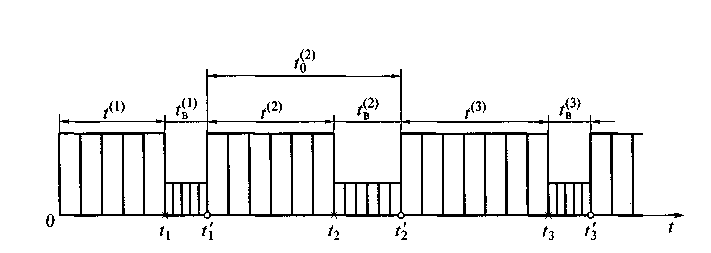
Рис. 3.2. Реалізація випадкового процесу експлуатації ремонтованого відновлюваного об'єкта першої групи:
![]() — значення
часу роботи між відмовами;
— значення
часу роботи між відмовами;
![]() —
значення часу відновлення (ремонту);
—
значення часу відновлення (ремонту);
![]() —
значення часу між
—
значення часу між
![]() та
та
![]() відновленнями;
відновленнями;
![]() —
моменти часу появи відмов
—
моменти часу появи відмов
![]() ;
;
![]() —
моменти часу відновлення
—
моменти часу відновлення
![]() .
.
В результаті ремонту об'єкт приводять в працездатний стан. Можливі періоди вимикання об'єкта, коли він не відмовляє і не відновлюється, виключаються з розгляду.
Таким чином, для
першої групи об'єктів в процесі
експлуатації чергуються випадкові
періоди часу безвідмовної роботи
![]() і часу відновлення
(ремонту)
і часу відновлення
(ремонту)![]() .
Зазвичай вважають, що випадкові величини
.
Зазвичай вважають, що випадкові величини
![]() мають однакові
розподіли (аналогічно і
мають однакові
розподіли (аналогічно і
![]() ).
Випадковий час між черговими відновленнями
(позначені кружками)
).
Випадковий час між черговими відновленнями
(позначені кружками)![]() .
.
Якщо випадкові
величини
![]() незалежні,
то щільність розподілу їх суми
незалежні,
то щільність розподілу їх суми
![]() за
відомим з теорії ймовірностей правилом
про композиції розподілів
за
відомим з теорії ймовірностей правилом
про композиції розподілів
![]()
де![]() —
щільність розподілу часу безвідмовної
роботи;
—
щільність розподілу часу безвідмовної
роботи;
![]() — щільність
розподілу часу відновлення (ремонту)
об'єкта. За аналогією з ремонтованими
невідновлювальної об'єктами можна
розглядати потік відновлень з параметром
— щільність
розподілу часу відновлення (ремонту)
об'єкта. За аналогією з ремонтованими
невідновлювальної об'єктами можна
розглядати потік відновлень з параметром
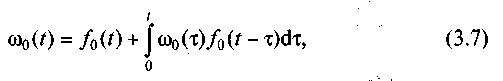
де
![]() —
щільність розподілу часу між черговими
відновленнями.
—
щільність розподілу часу між черговими
відновленнями.
Параметр потоку
відновлень
![]() і щільність
і щільність
![]() розподілу часу
до появи
розподілу часу
до появи
![]() відновлення (цей час дорівнює сумі
відновлення (цей час дорівнює сумі
![]() )
пов'язані наступним співвідношенням:
)
пов'язані наступним співвідношенням:
![]()
Надійність об'єктів
першої групи може бути оцінена за
допомогою миттєвих і числових показників.
Одним з миттєвих показників є параметр
потоку відновлень
![]() Проте зазвичай застосовують ймовірність
Проте зазвичай застосовують ймовірність
![]() застати об'єкт
працездатним (готовим до застосування)
в момент часу
застати об'єкт
працездатним (готовим до застосування)
в момент часу
![]() або ймовірність
або ймовірність
![]() того, що об'єкт
в момент часу
того, що об'єкт
в момент часу
![]() буде неработоспосооним
(буде знаходитися в стані змушеного
простою). залежність
буде неработоспосооним
(буде знаходитися в стані змушеного
простою). залежність
![]() називається
функцією
готовності.
називається
функцією
готовності.
Як ймовірність
![]() ,
так і
ймовірність
,
так і
ймовірність
![]() знаходяться в
припущенні, що при
знаходяться в
припущенні, що при
![]() об'єкт працездатний,
тобто:
об'єкт працездатний,
тобто:
![]()
![]()
Об'єкт може знаходитися в момент часу t в працездатному стані при здійсненні одного з двох несумісних подій:
1) об'єкт протягом часу (0, t) не відмовив;
2) об'єкт відмовляв і відновлювався і після останнього відновлення більше не відмовляв.
Ймовірність
![]() застати об'єкт
працездатним в момент часу t дорівнює
сумі ймовірностей появи зазначених
подій. Імовірність появи першої події
дорівнює ймовірності безвідмовної
роботи p(t)
об'єкта протягом часу (0, t).
застати об'єкт
працездатним в момент часу t дорівнює
сумі ймовірностей появи зазначених
подій. Імовірність появи першої події
дорівнює ймовірності безвідмовної
роботи p(t)
об'єкта протягом часу (0, t).
Для визначення
ймовірності появи другої події розглянемо
малий інтервал
![]() ,
що передує
,
що передує
![]() ,
Імовірність того, що на цьому інтервалі
закінчиться останній
,
Імовірність того, що на цьому інтервалі
закінчиться останній
![]() ремонт і об'єкт
більше не відмовить за час, що залишився
(t - τ),
дорівнює
ремонт і об'єкт
більше не відмовить за час, що залишився
(t - τ),
дорівнює
![]()
Підсумовуємо по всьому п = 1, 2, ... і отримуємо
![]()
де![]() —
параметр потоку відновлень.
—
параметр потоку відновлень.
Інтегруючи по τ від 0 до t знаходимо:
![]()
Таким чином, імовірність застати об'єкт працездатним в момент часу t
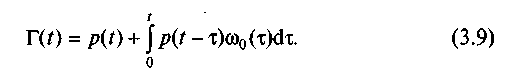
Застосуємо до формули (3.9) вузлову теорему відновлення (теорему Сміта), згідно з якою
![]()
де
![]() —
математичне сподівання числа відмов
на інтервалі
—
математичне сподівання числа відмов
на інтервалі
![]() — математичне
сподівання часу між черговими подіями
потоку;
— математичне
сподівання часу між черговими подіями
потоку;![]() —
незростаюча інтегрована на інтервалі
—
незростаюча інтегрована на інтервалі
![]() функція.
функція.
Врахуємо, що
математичне сподівання випадкової
величини
![]() дорівнює
дорівнює![]() та що
та що
![]()
Тоді отримаємо
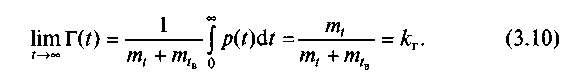
Таким чином,
імовірність
![]() пропрямує
пропрямує![]() до усталеного
значення
до усталеного
значення
![]() ,
не залежному від законів розподілу
випадкових величин
,
не залежному від законів розподілу
випадкових величин
![]() та
та![]() .
Величина
.
Величина![]() часто
ототожнюється з коефіцієнтом готовності,
який визначається як ймовірність того,
що об'єкт виявиться працездатним в
довільний момент часу, крім запланованих
періодів, протягом яких використання
об'єкта за призначенням не передбачається.
часто
ототожнюється з коефіцієнтом готовності,
який визначається як ймовірність того,
що об'єкт виявиться працездатним в
довільний момент часу, крім запланованих
періодів, протягом яких використання
об'єкта за призначенням не передбачається.
Відповідно до формули
(3.10) коефіцієнт
![]() готовності можна
розуміти як частку часу, протягом якого
об'єкт працездатний, від загального
часу експлуатації об'єкта.
готовності можна
розуміти як частку часу, протягом якого
об'єкт працездатний, від загального
часу експлуатації об'єкта.
Враховуючи загальні
властивості процесу відновлення, можна
відзначити особливість процесу наближення
![]() до усталеного
значення
до усталеного
значення
![]() при
фіксованих значеннях
при
фіксованих значеннях![]() та
та
![]() стаціонарний
режим наступає тим повільніше, чим менше
дисперсія випадкової величини
стаціонарний
режим наступає тим повільніше, чим менше
дисперсія випадкової величини
![]()
Часто використовують
середнє за термін служби
![]() значення
коефіцієнта готовності:
значення
коефіцієнта готовності:
![]()
при цьому![]()
Провівши міркування,
аналогічні наведеним раніше при виведенні
формули (3.9), можна отримати вираз для
визначення ймовірності
![]() того, що об'єкт
не тільки виявиться працездатним в
момент часу
того, що об'єкт
не тільки виявиться працездатним в
момент часу
![]() ,
але і пропрацює безвідмовно на заданому
інтервалі
,
але і пропрацює безвідмовно на заданому
інтервалі
![]() (іноді
цю ймовірність називають готовністю
на проміжку
(іноді
цю ймовірність називають готовністю
на проміжку
![]() або
оперативною готовністю):
або
оперативною готовністю):
![]()
Функцію готовності![]() можна
розглядати як частковий випадок
функції
можна
розглядати як частковий випадок
функції
![]() при.
при.![]() При τ=t
функція
При τ=t
функція![]()
![]() )
перетворюється
в умовну ймовірність безвідмовної
роботи об'єкта, знайдену в припущенні,
що в момент часу t об'єкт працездатний.
Усталене значення
)
перетворюється
в умовну ймовірність безвідмовної
роботи об'єкта, знайдену в припущенні,
що в момент часу t об'єкт працездатний.
Усталене значення
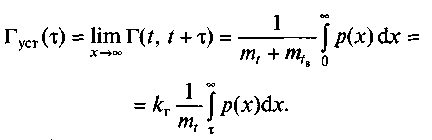 (3.13)
(3.13)
При довільних законах розподілу часу між відмовами і часу відновлення рішення рівнянь (3.12) і (3.13) зустрічає великі труднощі. Можуть бути використані чисельні методи; іноді виявляється зручним операційний метод.
Найбільше практичне значення має випадок, коли час між відмовами і час відновлення мають показові розподілу:
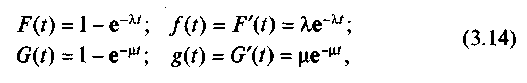
де![]() —
інтенсивність віднови.
—
інтенсивність віднови.
В результаті розв'язання рівнянь (3.9)—(3.13) отримаємо
![]()
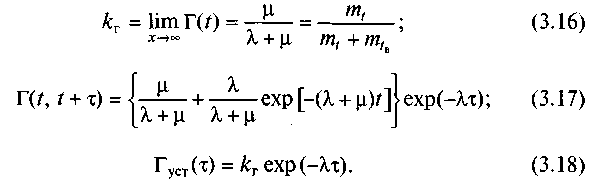
Формули (3.15) - (3.18), в основному, і використовуються при практичних розрахунках. Щоб повніше і наочніше розкрити зміст коефіцієнта готовності, отримаємо вираз (3.15), застосовуючи прийоми теорії масового обслуговування.
При допущеннях (3.14) процес зміни станів об'єкта буде марковским (тобто без післядії) процесом з безперервним часом і кінцевим безліччю станів: 0 - об'єкт працездатний; 1 - об'єкт непрацездатний, знаходиться в ремонті.
Знайдемо спочатку
ймовірність того, що об'єкт виявиться
працездатним в момент часу![]() Для позначення
ймовірностей знаходження в певних
станах у момент
Для позначення
ймовірностей знаходження в певних
станах у момент
![]() будемо застосовувати
прописні букви
будемо застосовувати
прописні букви
![]() на відміну від
ймовірності безвідмовної роботи протягом
часу від
на відміну від
ймовірності безвідмовної роботи протягом
часу від
![]() що
позначається
що
позначається![]() Шукана подія може бути здійснена двома
наступними несумісними способами:
Шукана подія може бути здійснена двома
наступними несумісними способами:
працездатний до моменту часу
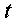 об'єкт залишиться
працездатним протягом інтервалу часу
об'єкт залишиться
працездатним протягом інтервалу часу
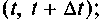
непрацездатний (що знаходиться в ремонті) до моменту часу t об'єкт буде відновлено протягом інтервалу часу
Всі інші можливості
мають ймовірність більш високого порядку
малості, ніж
![]()
Імовірність першої з зазначених подій
![]()
де![]() —
ймовірність застати об'єкт в момент
часу в стані 0;
—
ймовірність застати об'єкт в момент
часу в стані 0;
![]() -
нескінченно мала в порівнянні з
-
нескінченно мала в порівнянні з
![]() величина.
величина.
Оскільки сума ймовірностей станів 0 та 1
![]()
то ймовірність другої події
![]()
Отже, ймовірність того, що до моменту часу t + Δt об'єкт виявиться працездатним,
![]()
Звідки заключаємо, що
![]()
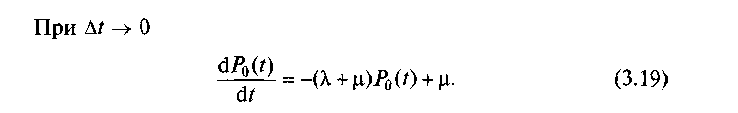
![]()
![]()
![]()
![]() ,
що зазвичай і буває на практиці,
,
що зазвичай і буває на практиці,![]()
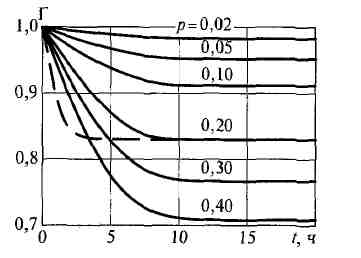
На рис. 3.3 показана
залежність функції готовності
![]() від
коефіциієнта
від
коефіциієнта![]() При
збільшенні значення
При
збільшенні значення
![]() надійність
об'єкта знижується, але стаціонарний
режим встановлюється більш швидко. Якщо
формулу (3.15) переписати у вигляді
надійність
об'єкта знижується, але стаціонарний
режим встановлюється більш швидко. Якщо
формулу (3.15) переписати у вигляді
![]()
то очевидно, що тривалість перехідного процесу визначається також величиною µ: чим більше µ, тим швидше наступає стаціонарне значення.
Рис.
3.3. Функції готовності![]() при
показових розподілах часу безвідмовної
роботи і часу відновлення
при
показових розподілах часу безвідмовної
роботи і часу відновлення
Наведені на рис. 3.3
графіки відповідають
![]() Відповідна
залежність для
Відповідна
залежність для
![]()
![]() при
при![]() проведена
на рис. 3.3 пунктиром.
проведена
на рис. 3.3 пунктиром.
При
![]() й більших
значеннях
й більших
значеннях![]() (
системи з високим
рівнем безвідмовності і ремонтопридатності)
тривалість перехідного процесу для
(
системи з високим
рівнем безвідмовності і ремонтопридатності)
тривалість перехідного процесу для
![]() визначається в
основному значенням µ.
визначається в
основному значенням µ.
![]() Формулу
(3.15) можна перетворити з урахуванням
того, що
Формулу
(3.15) можна перетворити з урахуванням
того, що
и значення![]() .
визначається формулою (3.16):
.
визначається формулою (3.16):
![]()
![]() ,
,![]() в початковий
період експлуатації об'єкта значення
Г (t) наближено дорівнюють значенням
ймовірності безвідмовної роботи
в початковий
період експлуатації об'єкта значення
Г (t) наближено дорівнюють значенням
ймовірності безвідмовної роботи
![]() на
інтервалі
на
інтервалі
![]() .
У цьому можна
переконатися, якщо у формулах для
.
У цьому можна
переконатися, якщо у формулах для
![]() та
та
![]() розкласти
експоненти в ряди, в яких залишити лише
лінійні члени.
розкласти
експоненти в ряди, в яких залишити лише
лінійні члени.
При цьому виходить,
що при малих
![]() функція готовності
буде визначатися наступним виразом:
функція готовності
буде визначатися наступним виразом:![]()

Щоб уникнути
трудомістких обчислень значень
![]() в нестаціонарний
період, запропоновано наближено вважати,
що до певного моменту часу
в нестаціонарний
період, запропоновано наближено вважати,
що до певного моменту часу
![]() ,
при якому імовірність безвідмовної
роботи
,
при якому імовірність безвідмовної
роботи
![]() ,
значення збігаються
,
значення збігаються
![]() с, а
с, а![]() при
при
![]() — рівні
— рівні![]() (рис.
3.4).
(рис.
3.4). 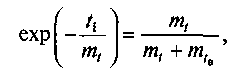
![]() При
цьому максимальна похибка буде в точці
tu
яку знайдемо
з умови
При
цьому максимальна похибка буде в точці
tu
яку знайдемо
з умови
Звідки t1=-mt lnkг
Підставимо це значення t в формулу (3.20), після перетворень одержимо:
![]()
При цьому максимальна відносна похибка обчислень
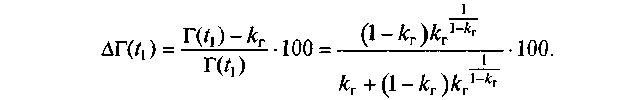
![]() близьке до одиниці
близьке до одиниці
![]()
![]() похибка
не велика і швидко зменшується з ростом
kτ.
похибка
не велика і швидко зменшується з ростом
kτ.
Наведені на рис. 3.3
і 3.4 залежності
мають місце при
![]() При розподілах
часу безвідмовної роботи, що відрізняються
від показового, часто існує провал
функції готовності на початковій
ділянці, коли
При розподілах
часу безвідмовної роботи, що відрізняються
від показового, часто існує провал
функції готовності на початковій
ділянці, коли
![]() має
вигляд, показаний на рис. 3.5. На рис. 3.5
можна виділити три характерні точки
кривої
має
вигляд, показаний на рис. 3.5. На рис. 3.5
можна виділити три характерні точки
кривої
![]()
На ділянці![]() функція готовності
незначно відрізняється від ймовірності
безвідмовної роботи об'єкта за час
функція готовності
незначно відрізняється від ймовірності
безвідмовної роботи об'єкта за час
![]() У тих випадках, коли вдається знайти
межу допустимого наближення, можна
вважати
У тих випадках, коли вдається знайти
межу допустимого наближення, можна
вважати
![]()
В точці![]() функція
функція![]() досягає
мінімального значення.
досягає
мінімального значення.
Величина провалу
![]() функції готовності
залежить від законів розподілу часу
безвідмовної роботи і часу відновлення.
Задача визначення
функції готовності
залежить від законів розподілу часу
безвідмовної роботи і часу відновлення.
Задача визначення
![]() вирішена
аналітично лише
для випадку, коли закон розподілу часу
безвідмовної роботи може бути описаний
суперпозицією показових розподілень
(при цьому враховується наявність
періоду
вирішена
аналітично лише
для випадку, коли закон розподілу часу
безвідмовної роботи може бути описаний
суперпозицією показових розподілень
(при цьому враховується наявність
періоду
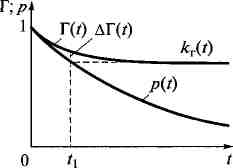
Рис.
3.4. Залежність![]() и p{t)
и p{t)
![]()
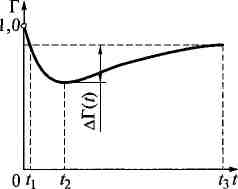
Рис. 3.5. Нестаціонарна ділянка функції готовності системи, у якій розподіл часу безвідмовної роботи описується суперпозицією двох показових розподілень.
припрацювання) і
час відновлення розподілено по показовому
закону. При цьому встановлено, що більш
крутому спаду початкового ділянки
![]() відповідає більш
глибокий провал функції
відповідає більш
глибокий провал функції
![]() Крім того, значення провалу і його
тривалість зростають при збільшенні
безвідмовності системи. Тому негативне
впливавня процесу прироблення на функцію
готовності найбільш сильно проявляється
в високо надійних системах.
Крім того, значення провалу і його
тривалість зростають при збільшенні
безвідмовності системи. Тому негативне
впливавня процесу прироблення на функцію
готовності найбільш сильно проявляється
в високо надійних системах.
Поряд з коефіцієнтом
готовності часто застосовують коефіцієнт
технічного використання![]() —
відношення математичного очікування
часу перебування об'єкта в працездатному
стані за деякий період експлуатації до
суми математичних очікувань часу
перебування об'єкта в працездатному
стані, часу простоїв, обумовлених
технічним обслуговуванням, і часу
ремонту за той же період експлуатації.
Очевидно, що завжди
—
відношення математичного очікування
часу перебування об'єкта в працездатному
стані за деякий період експлуатації до
суми математичних очікувань часу
перебування об'єкта в працездатному
стані, часу простоїв, обумовлених
технічним обслуговуванням, і часу
ремонту за той же період експлуатації.
Очевидно, що завжди![]()
Припустимо, що простої можуть бути лише двох видів: аварійні при відновленні працездатності об'єкта після відмови і планові (профілактичні).
Якщо середнє число
відмов за період експлуатації![]() дорівнює Ω, то загальний час експлуатації
складається з трьох складових:
дорівнює Ω, то загальний час експлуатації
складається з трьох складових:
часу знаходження в працездатному стані - тривалість
часу знаходження в аварійному ремонті - тривалість
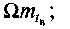
часу знаходження в плановому ремонті - тривалість
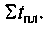
Отже,
![]()
Коефіцієнт технічного використання
![]()
![]()
Підставивши у формулу (3.21) замість його вираз , згідно з формулою (3.16) отримаємо:
![]()
Надійність відновлюваних об'єктів, в яких відмови неприпустимі, а можливий ремонт деяких елементів під час виконання завдання, найчастіше оцінюють за допомогою умовної ймовірності безвідмовної роботи p(tі, tj) протягом заданого інтервалу часу (tі, tj) за умови, що в початковий момент часу всі елементи працездатні. Слово «умовна» зазвичай опускають.
Відмінність![]() від
відповідного показника для неремонтуємого
об'єкта полягає в тому, що при обчисленні
від
відповідного показника для неремонтуємого
об'єкта полягає в тому, що при обчисленні
![]() враховується ремонт елементів, які
відмовили при працездатному об'єкті
(системі). Зазвичай оцінка
враховується ремонт елементів, які
відмовили при працездатному об'єкті
(системі). Зазвичай оцінка
![]() для зпроектованих
об'єктів проводиться при допущенні про
показових розподілах часу безвідмовної
роботи і часу відновлення елементів.
Розрахунок таких систем описаний в гл.
4.
для зпроектованих
об'єктів проводиться при допущенні про
показових розподілах часу безвідмовної
роботи і часу відновлення елементів.
Розрахунок таких систем описаний в гл.
4.
Для об'єктів другої групи, в якості показників надійності, можуть також використовуватися параметр потоку відмов, наробка на відмову та інші характеристики.
Всі розглянуті в цій главі показники надійності об'єктів можна розділити на три групи:
інтервальні, відносяться до заданому інтервалу напрацювання або часу (t1, t2);
миттєві, відповідні заданому значенню часу або напрацювання
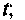
числові, не пов'язані з розташуванням заданого інтервалу або моменту часу (напрацювання), див. Таблицю 3.2.
Таблица 3.2
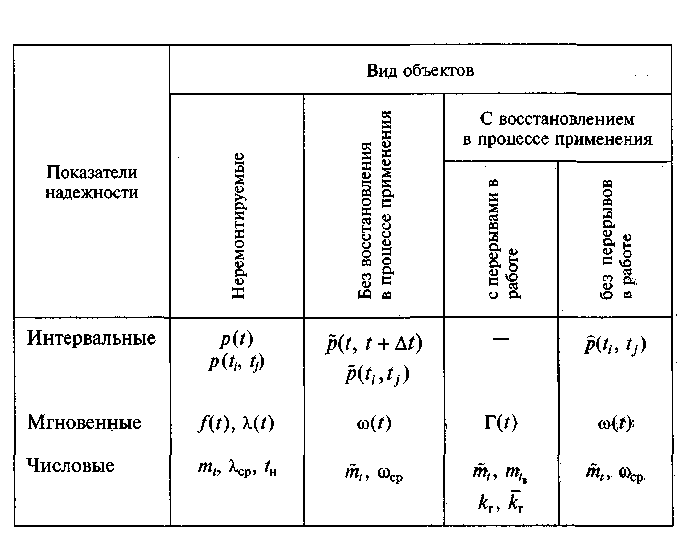
Основні показники надійності зведені в табл. 3.2. Сюди не включені показники, пов'язані з умовними розподілами напрацювання між відмовами ремонтованих невідновлювальних в процесі застосування об'єктів. Ці показники аналогічні показниками надійності неремонтуємих виробів і повинні бути доповнені моментами зв'язку або коефіцієнтами кореляції напрацювання між відмовами.
