Глава 3

НАДІЙНОСТІ РЕМОНТОВАНИХ ОБ'ЄКТІВ

3.1. Показники надійності ремонтованих об'єктів, не відновлюваних в процесі застосування

Показники надійності таких об'єктів обчислюються за напрацюванням. Сумарне напрацювання до виникнення n-ї відмови

д е Т⁽ⁱ⁾ — напрацювання між (i-1)-ю та i-ю відмовами.

Можливі два шляхи оцінки надійності ремонтованих об'єктів:

1. обчислення характеристик потоку відмов;

2. обчислення умовних розподілів напрацювання між відмовами.

В даний час найбільш поширене обчислення характеристик потоку відмов. Розглядаються потоки випадкових подій, кожна з яких складається в появі відмови об'єкта.

Потік відмов можна характеризувати основною функцією потоку Ω(t) — математичним сподіванням кількості відмов на інтервалі (0, t). Однак частіше в якості показника надійності використовують параметр потоку відмов - щільність ймовірності виникнення відмови об'єкта, що ремонтується, визначену для розглянутого моменту сумарної напрацювання. Це визначення потребує пояснення.

У теорії масового обслуговування при вивченні потоків подій застосовують дві характеристики:

1) інтенсивність потоку подій:

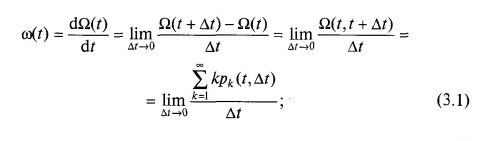
2) параметр потоку подій, д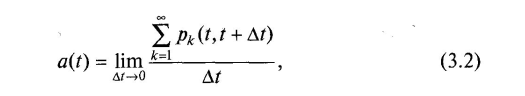 е p_k(t, t+Δt) - ймовірність появи рівно k подій на інтервалі (t, t+Δt).

Потоки відмов є одинарними потоками, тобто ймовірність суміщення в один і той же момент двох відмов пренебрежимо мала. Інакше кажучи,

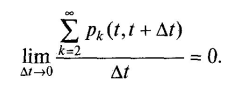
Для ординарних потоків відмов вирази (3.1) і (3.2) спрощуються, інтенсивність і параметр потоку відмов збігаються:

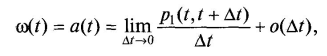
де р1(t, t+Δt) — ймовірність появи однієї відмови на інтервалі (t, t+Δt); o(t) — нескінченно мала величина більш високого порядку малості, ніж Δt (ймовірність появи двох і більше відмов на інтервалі (t, t+Δt) ).

Щоб не плутати інтенсивність відмов ремонтованих виробів з інтенсивністю відмов неремонтуємих виробів, застосовують термін «параметр потоку відмов». Зазвичай розглядають дві математичні моделі випадкових потоків відмов.

1. Кількісний опис ординарних потоків відмов є найбільш простим за відсутності наслідків. У першій моделі приймається, що ймовірність появи відмов об'єктів в будь-якому інтервалі напрацювання (t1, t2) не залежить від появи відмов в інших інтервалах напрацювання, не перетинаються з даним інтервалом. Для ординарних без післядії (пуассонівських) потоків відмов ймовірність безвідмовної роботи об'єкта на інтервалі (t1, t2)

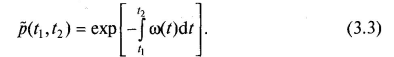
Прийнято вважати, що пуассонівський потік відмов характерний для складних нерезервованих систем, що складаються з високонадійних елементів, потоки відмов яких є незалежними. Якщо система «добре спроектована», то немає окремих малонадійних елементів, значення параметра потоку відмов яких співмірні зі значеннями параметра потоку відмов всієї системи. Для такої системи появу відмов на одному інтервалі напрацювання майже не впливає на ймовірність появи якого-небудь числа відмов на іншому інтервалі, не пересічному з першим.

П ри стаціонарному ω = const, потоці відмов без наслідків, ймовірність безвідмовної роботи на інтервалі Δt.

2. Іноді допущення про відсутність післядії є занадто грубим. Тоді в якості другого варіанту моделей реальних потоків відмов можуть розглядатися потоки відмов з обмеженим післядією, в яких значення напрацювання між послідовними відмовами є незалежними випадковими величинами. Обмежена післядія проявляється в тому, що ймовірність появи відмови на напрацювання (t1, t2) залежить від напрацювання, накопиченого від останнього відмови, і не залежить від того, коли відбулися попередні відмови. Якщо випадкові величини напрацювання між відмовами розподілені і незалежні, то параметр потоку відмов пов'язаний з щільністю розподілу напрацювання між відмовами f(t) рівняням

Ц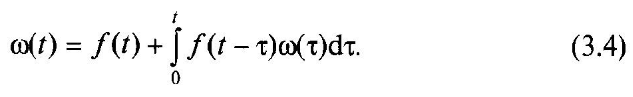 е рівняння може бути отримано шляхом наступних розмірковувань. Нехай при відмові об'єкта він миттєво відновлюється, здобуваючи властивості нового об'єкта (або замінюється на новий). Середнє число відмов (замін) n на інтервалі (t, t+dt) пропорційно числу N об'єктів, які знаходяться під спостереженням і тривалості інтервалу напрацювання dt

де n₁ — кількість відмов об’єктів з числа безвідмовно пропрацювавших на інтервалі (0, t); n₂ — число відмов об'єктів з числа тих, що вже відмовили раніше.

Очевидно, що n₁=N*f(t)dt.

Для визначення середнього числа відмов об'єктів з числа тих, що вже відмовили раніше візьмемо малий інтервал напрацювання (τ, τ + dτ), що передує t. Протягом цього інтервалу відмовило і замінено на нові Nω(τ)dτ об'єктів. З них в інтервалі (t, t + dt) будуть знову замінені [Nω(τ)dτ] f(t-τ)dt. Підсумовуючи по всіх τ від 0 до t, отримуємо, що всього з числа тих, що вже відмовили (замінені) до моменту часу t об'єктів знову відмовлять на інтервалі (t, t + dt).

О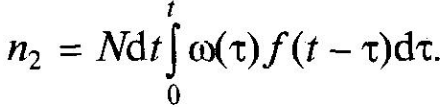 бщее среднее число отказов на интервале наработки (t, t+dt)

П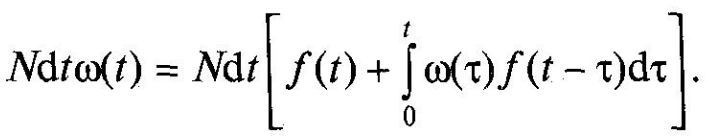 ри скороченні на Ndt отримуємо рівняння (3.4)

.

Таким чином, параметр потоку відмов пов'язаний з щільністю розподілу напрацювання між відмовами інтегральним рівнянням Вольтера другого роду з різницевим ядром. Це рівняння не завжди вдається вирішити в кінцевому вигляді. У деяких випадках зручно шукати рішення, користуючись перетворенням Лапласа. При цьому

д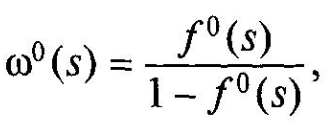 е ω⁰(s) — перетворення Лапласа функції ω(t),

f⁰(s) — перетворення Лапласа функції f(t).

У загальному випадку рівняння (3.4) інтегрується чисельно. При цьому можна використовувати метод послідовних наближень. Відповідно до цього методу ппроводяться послідовні обчислення за формулою

до тих пір, поки значення ω_i(t) и ω_i+1(t) стануть практично збігатися. В якості нульового наближення зручно брати інтенсивність відмов λ (у). Якщо наробіток між відмовами має показове розподіл

f (t) = λ ехр (-λt), то ω = λ = const. У технічних завданнях на проектовані об'єкти часто використовують середній показник

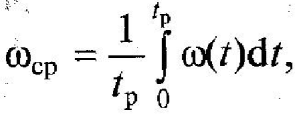
де t_р — технічний ресурс об'єкта.

Якщо при t → ∞ щільність розподілу наробітку до відмови f (t) → 0, то

існує усталене значення параметра потоку відмов

де ~m_t, — напрацювання на відмову ремонтованого об'єкта (у розглянутому випадку збігається із середньім напрацюванням до відмови ~m_t = m_t).

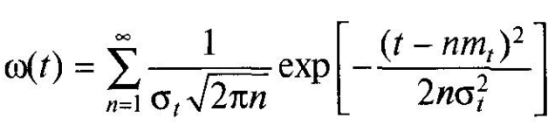У загальному випадку напрацювання на відмову ~m_t, являє собою відношення напрацювання об'єкта, що ремонтується до математичного сподівання числа його відмов протягом цього напрацювання. Часто ~m_t використовується в якості самостійного показника надійності. Якщо наробіток виражається в одиницях часу, то може застосовуватися термін «середній час безвідмовної роботи». При нормальному розподілі напрацювання між відмовами параметр потоку відмов

де ~m_t, σ_t — середнє значення і середнє квадратичне відхилення напрацювання між відмовами.

2т, 2 т, 4т,

На рис. 3.1 видно, що графік параметра потоку відмов здійснює ряд загасаючих коливань, наближаючись до значення ῶ=1/m_t.

200

0

400

т,

б

Рис. 3.1. Параметр потока отказа объектов:

а — при нормальном распределении; б — при альфа-распределении наработки до отказа

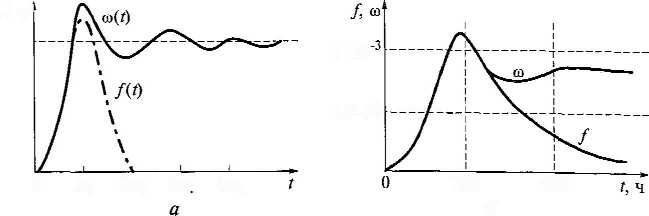
Тривалість цього коливального процесу обернено пропорційне середньому квадратичному відхиленню напрацювання між відмовами σ_t. Чим менше σ_t, тим виразніше відмови групуються біля середніх значень m_t, і тим більша сумарне напрацювання повиннt накопичитися, перш ніж зрівняються умови появи відмов. При σ_t = 0 відмови відбуваються регулярно, і усталене значення ῶ взагалі не досягається.

Таким чином, якщо розглянутий інтервал напрацювання обраний достатьо далеко від початку експлуатації об'єктів даного типу, то параметр потоку відмов можна вважати стаціонарним.

Початкові (при t = 0) і що встановилися (при t → ∞) значення параметра потоку відмов при деяких найбільш уживаних розподілах напрацювання між відмовами наведено в табл. 3.1.

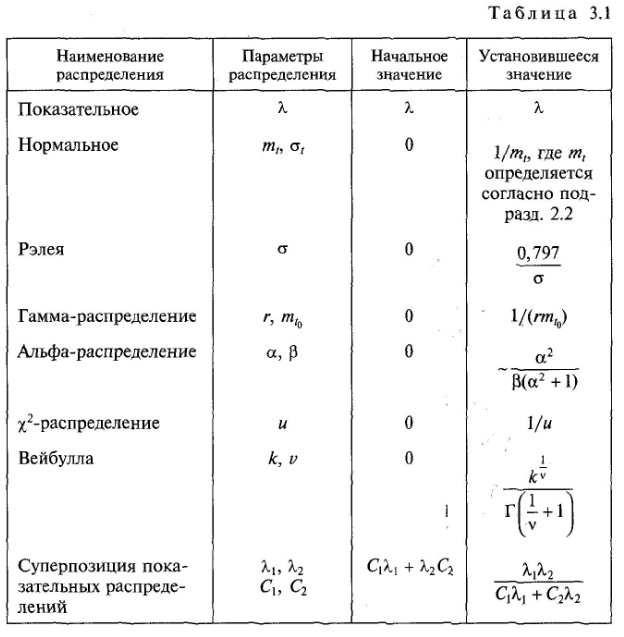
При обчисленні умовних розподілів напрацювання між відмовами можна відраховувати напрацювання від моменту закінчення відповідного ремонту або крупного профілактичного заходу.

Показники надійності в розглянутому випадку ті ж, що і для не ремонтованих об'єктів, але вони є умовними, тобто обчислюються за умови, що сталося певне число відмов. Ці показники надійності характеризують розподіл випадкової величини - напрацювання між i-ю та (i + 1)-ю відмовами.

Якщо із збільшенням сумарної напрацювання спостерігаються все більш серйозні відмови, то іноді доцільно розглядати об'єкт, що ремонтується, як неремонтуємий, і знаходити кілька розподілів напрацювання до відмови, відповідних різними визначеннями непрацездатного стану, наприклад:

• розподіл напрацювання до першої відмови;

• розподіл наробітку до дрібного ремонту;

• розподіл наробітку до середнього ремонту;

• розподіл напрацювання до капітального ремонту і т.д.