2.2. Теоретичні розподіли наробітку до відмови

У якості теоретичних розподілів наробітку до відмови можуть бути використані будь-які застосовувані в теорії ймовірностей безперервні розподіли. У принципі можна побрати будь-яку криву, площа під якою дорівнює одиниці, і використовувати її як криву розподілу випадкової величини.

На мал. 2.3 наведені графіки / і / для чотирьох найбільше часто вживаних у теорії ймовірностей розподілів, а відповідні функції надійності — на мал. 2.4.

Показове (експонентне) розподіл. При показовому розподілі наробітку до відмови

Дисперсія наробітку до відмови /

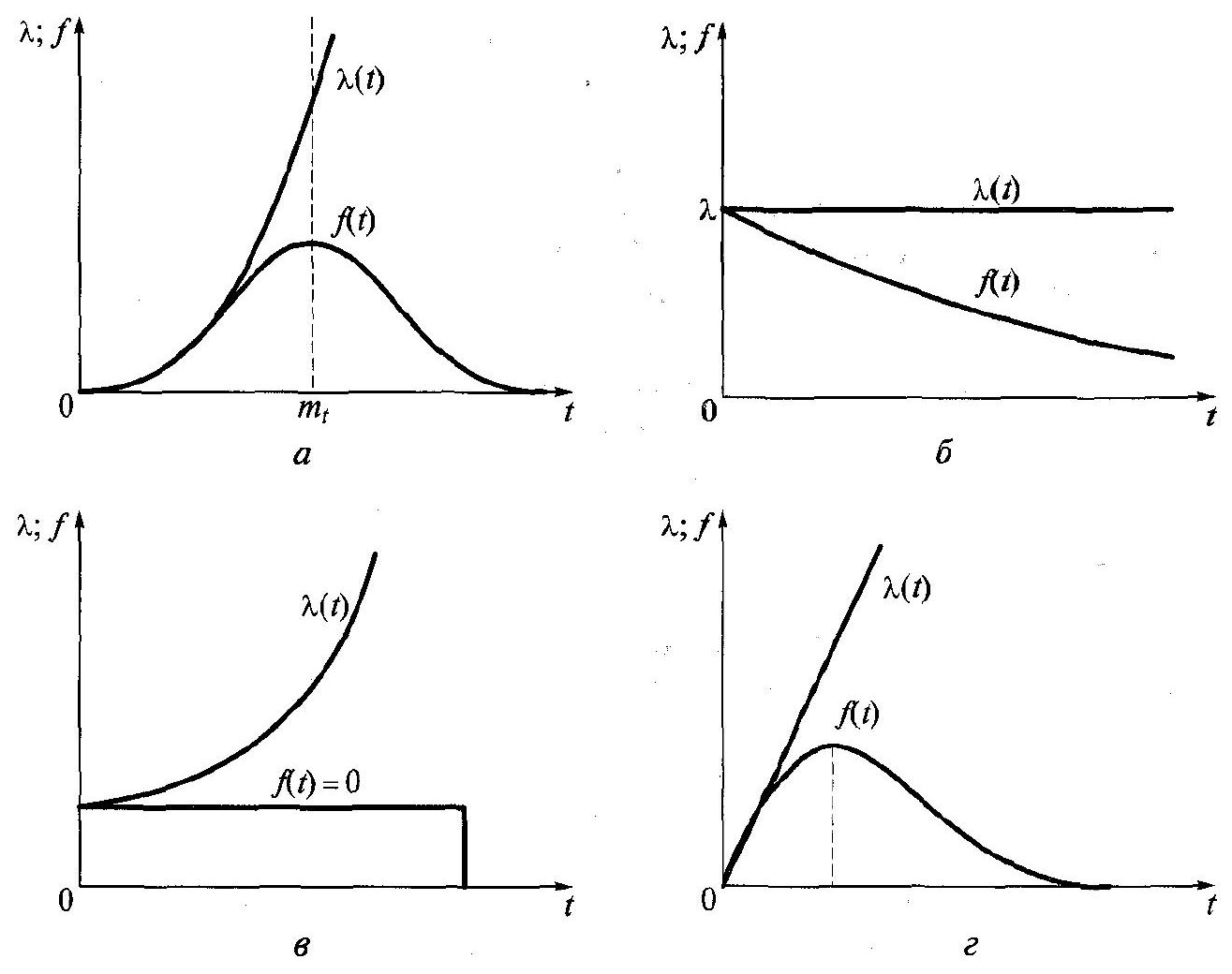
Рис. 2.3. Графіки / і / теоретичних законів розподілу наробітку до відмови:

— нормальне (усічене на інтервалі ) розподіл; б — розподіл рівномірної щільності; в — показовий розподіл; г — розподіл Рэлея

Показовий розподіл застосовується частіше інших при дослідженні надійності виробів. Це пояснюється рядом причин.

По-перше, показовий розподіл наробітку до відмови типово для складних об'єктів, що полягають із багатьох елементів з різними розподілами наробітку до відмови. Крім того, для деяких об'єктів можна усунути підвищену інтенсивність відмов у початковий період експлуатації застосуванням тренування. Якщо в процесі

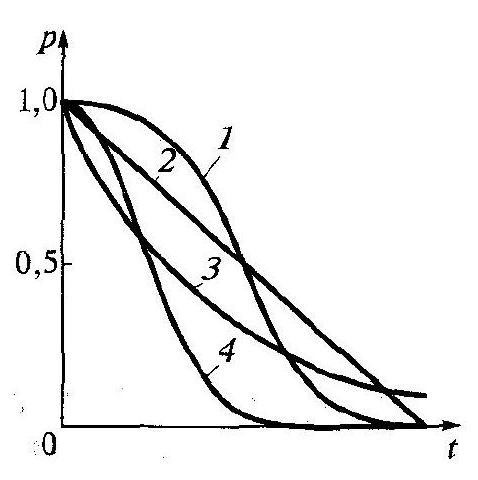
Рис. 2.4. Графіки функцій надійності:

1 — нормальне (усічене на інтервалі розподіл); 2 — розподіл рівномірної щільності; 3 — показовий розподіл; 4 — розподіл Рэлея.

експлуатації цих об'єктів немає періоду значного зношування, то інтенсивність відмов можна приблизно вважати постійної.

По-друге, при постійних интенсивностях відмов виробів виходять дуже прості формули для розрахунків надійності. Це пов'язане з тим, що при/імовірність безвідмовної роботи протягом заданого наробітку/не залежить від сумарного наробітку.

По-третє, при обмежених експериментальних даних важко виявити значні відхилення від гіпотези/ навіть якщо і є можлива нестаціонарність/. Якщо експериментальних даних недостатньо, щоб виявити дійсний характер нестаціонарності/, у якості першого наближення ухвалюють/

Усічений нормальний розподіл. При нормальному (гауссовом) розподілі випадкової величини вона може ухвалювати будь-які значення від/ до/. Оскільки можливі значення випадкового наробітку до відмови/можуть бути тільки позитивними, розподіл/може бути лише усіченим нормальним.

Усіченим нормальним розподілом випадкової величини називається розподіл, одержуване з нормального при обмеженні інтервалу можливих значень цієї величини. Тому що можливі значення випадкової величини/обмежені інтервалом/, те щільність усіченого розподілу

де/- щільність неусіченого розподілу;

//;

/- множник, що нормує, перебуває з умови, що площа під кривой розподілу дорівнює одиниці, тобто

Або

Підставивши у формулу (2.16) вираження для/і застосувавши підстановку, знаходимо

де/- середнє значення й середнє квадратическое відхилення неусіченого розподілу відповідно. Після перетворення одержимо

де — нормована функція Лапласа; .

Таблиця значень цієї функції наведена в довідниках.

Функція надійності

Інтенсивність відмов

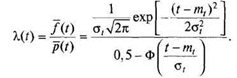
Знайдемо формули для числових характеристик усіченого нормального розподілу: математичного очікування наробітку до відмови/і дисперсії наробітку до відмови/. Згідно з визначеннями цих характеристик

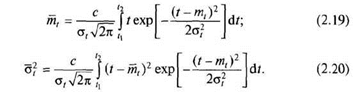
Провівши перетворення, маємо

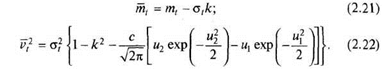
У формулах (2.21) і (2.22) коефіцієнтом/позначене:

Коли можливі значення випадкової величини/лежать в інтервалі/, з формул (2.17), (2.19) ( (2.23) одержуємо

У формулі (2.26) коефіцієнт

На мал. 2.5 наведені залежності відносин числових характеристик усіченого й неусіченого нормального розподілів і значення множника, що нормує, / від відношення/ На малюнку видне, що при значеннях/( що звичайно й

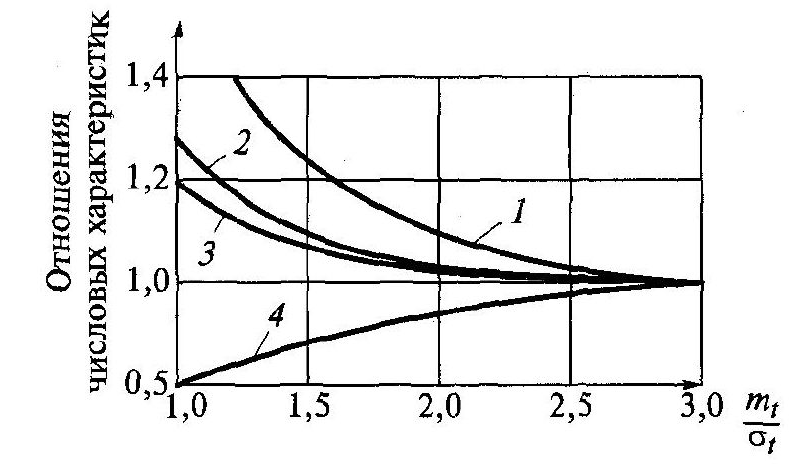
Рис. 2.5. Залежність відносин числових характеристик усіченого й неусіченого нормального розподілу множника, що й нормує, / від відношення(риса над/ означає , що ці характеристики ставляться до усіченого розподілу):

має місце на практиці при вживанні нормального розподілу) значення з₀ дуже мало відрізняється від одиниці й . Тому надалі не будемо додавати термін «усічене» до назви «нормальний розподіл наробітку до відмови». Необхідно відзначити, що всупереч поширеній думці при відмовах елементів за рахунок зношування розподіл наробітку до відмови буде далеко не завжди нормальним. Необхідною умовою нормального розподілу наробітку до відмови є малий розкид значень швидкості зношування елементів.

Через велике теоретичне й прикладне значення нормального розподілу його намагаються іноді застосувати й при явно несиметричних розподілах наробітку до відмови. Для цього підбирають деяку функцію випадкового наробітку до відмови, наприклад/ і т.д., що приблизно випливає нормальному закону. Наприклад, досить часто використовується логарифмічно нормальний розподіл усталостной довговічності, при якому передбачається, що логарифм числа циклів навантаження до руйнування зразка розподілений за нормальним законом.

Розподіл Рэлея. Для розподілу Рэлея

Параметр розподілу Рэлея, звичайно позначуваний , є модою цього розподілу. Його не потрібно плутати із середнім квадратическим відхиленням . Для розподілу Рэлея математичне очікування

дисперсія

Гамма-розподіл. Щільність гамма-розподілу де/- гамма-функція; /

У теорії надійності гамма-розподіл звичайний використовується при цілому При гамма-розподіл є показовим розподілом. У цьому випадку показовий розподіл  цей розподіл наробітку до першої відмови. При цілому гамма-розподіл є розподілом суми незалежних випадкових величин, кожна з яких має показовий розподіл з параметром Гамма-розподіл при цілому іноді називають розподілом Эрланга. Для такого розподілу

Математичне очікування наробітку до відмови

Дисперсія

Графіки гамма-розподілу наведені на мал. 2.6.

При більших значеннях/гамма-розподіл сходиться до нормального розподілу з параметрами

Розподіл Вейбулла. Криві цього розподілу наведені на мал. 2.7. Щільність розподілу Вейбулла:

Розподіл Вейбулла має два параметри:/і/ Параметр /визначає масштаб; при його зміні крива розподілу стискується або розтягується.

При розподіл Вейбулла перетворюється в показовий розподіл. Звичайно значення _V вибираються в межах від 1 до 2.

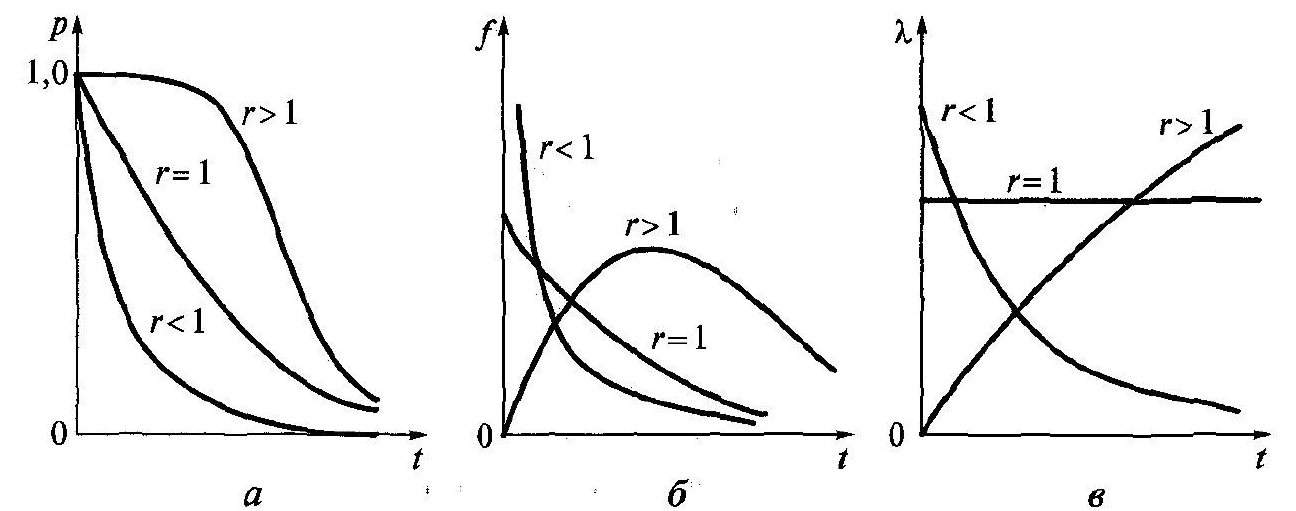
Рис. 2.6. Графіки гамма-розподілу: а — функції надійності; 6 — криві розподілу наробітку до появи г відмов; в — інтенсивності відмов

Для розподілу Вейбулла функція надійності/і інтенсивність відмов/описуються наступними формулами:

Математичне очікування наробітку відмови

де/ ( гамма-функція;

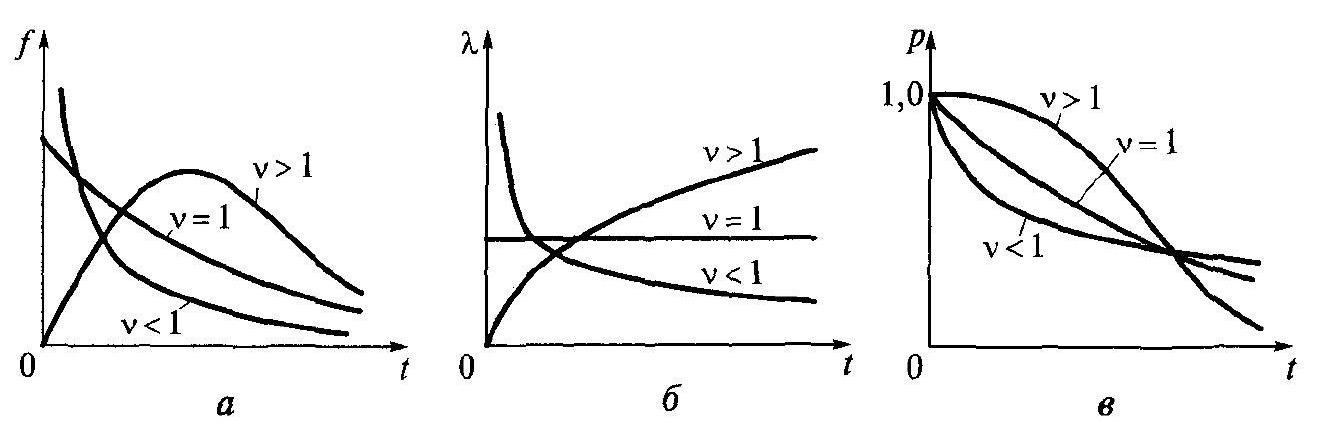
Рис. 2.7. Графіки розподілу Вейбулла при а — криві розподілу; б — інтенсивності відмов; в — функції надійності.

Розподіл Вейбулла іноді використовується для опису надійності кулькових підшипників і деяких типів електронних ламп/

Більш докладні відомості про згадані раніше теоретичні розподіли можна знайти у відповідних курсах теорії імовірності.

Трикутний розподіл. Трикутний розподіл у загальних курсах теорії ймовірностей не розглядається. Цей розподіл характеризує випадкові величини, що мають обмежену область можливих значень . Положення й форму трикутного розподілу характеризують три параметри: — границі області можливих значень; — мода (мал. 2.8).

Якщо позначити значення щільності розподілу в крапці моди /то

Щільність розподілу

Рис. 2.8. Трикутний розподіл випадкової величини: а — графіки щільності розподілу і інтенсивності відмов ; 6 — графік функції надійності .

Функція надійності

Інтенсивність відмов

У деяких завданнях у якості параметрів розподілу зручно використовувати також швидкості зміни щільності розподілу:

Медіана/трикутного розподілу може бути знайдена з рівняння

у результаті розв'язку якого одержимо

Математичне очікування

Зробивши підстановку

можна перейти до нормованого трикутного розподілу. При цьому/відповідає/відповідає/

Позначивши

після перетворень одержимо

Функція надійності може бути виражена через допоміжну функцію/ у такий спосіб:

де нормована функція розподілу

На мал. 2.9 наведені графіки при різних значення параметра Значення функції надійності, що відповідають певним можна також обчислити по

табл. 2.1.

Сума (суперпозиція) розподілів. Щоб одержати теоретичний розподіл, близьке до експериментального, іноді застосовують наступне приймання. Щільність розподілу наробітку до відмови вважається рівній сумі:

Де /- коефіцієнти ваги, що враховують вплив різних, що складаються,/

/- теоретичні розподіли певного виду.

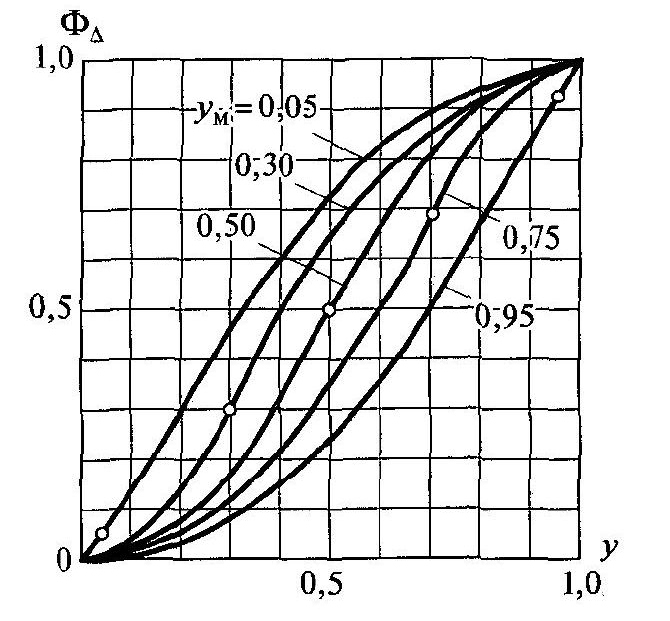
Рис. 2.9. Значення нормованої функції розподілу/(крапками на кривих відзначені значення /).

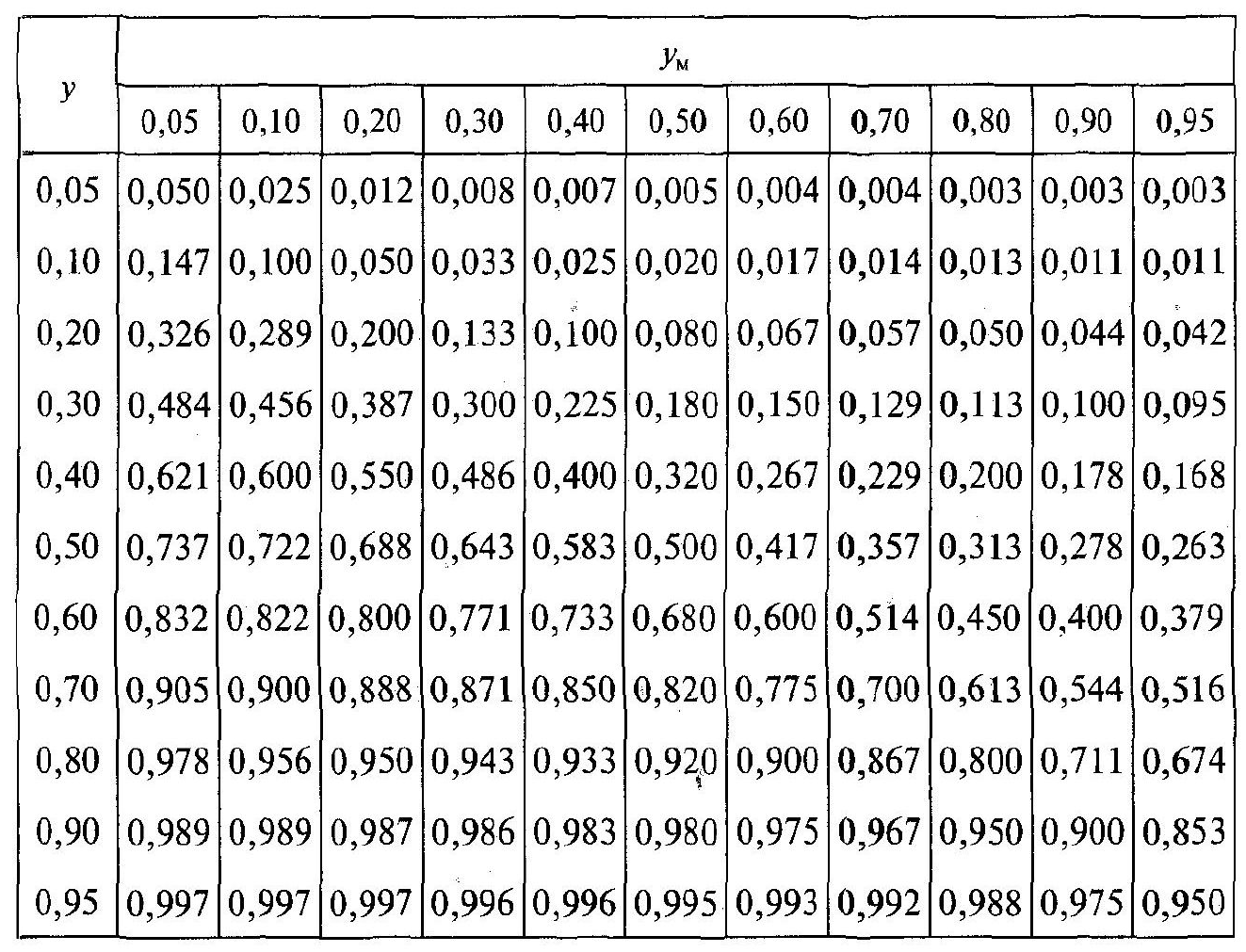
Таблиця 2.1

Розглянемо як приклад суму (суперпозицію) двох показових розподілів

Для цього випадку маємо

Відповідний графік/наведений на мал. 2.10.

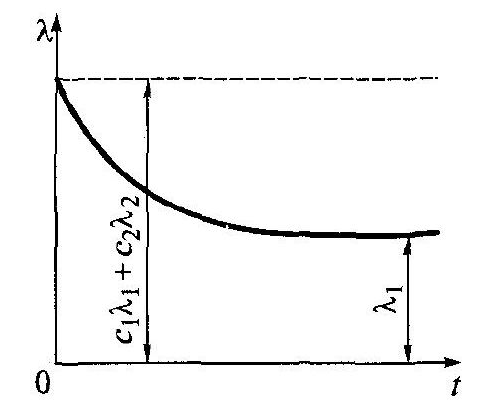
Рис. 2.10. Графік/ для суми (суперпозиції) двох показових розподілів

Середній наробіток до відмови

Нехай для визначеності , Тогдадля дуже більших члени, що містять , малі . При малих / значення/і/близькі до одиниці й/.

Про вибір типу теоретичного розподілу наробітку до відмови. Для вибору типу теоретичного розподілу наробітку до відмови доцільно використовувати інформацію про зміни в об'єктах перед виникненням відмов. Для цього необхідно знать у результаті яких фізичних процесів з'являється відповідний розподіл. Інакше кажучи, обраному теоретичному розподілу наробітку до відмови повинна відповідати певна модель наближення об'єкта до відмови. Бажане, щоб ці моделі були фізичними, тобто узагальнювали основні особливості фізичних процесів наближення до відмов (а також допускали можливість відтворення цих процесів у лабораторії).