14. Касательная плоскость и нормаль к поверхности
Для данных поверхностей найти уравнения касательных плоскостей и нормалей в указанных точках
14.1
14.2
14.3
14.4
14.5
14.6
14.7
14.8
15. Исследование на экстремум функций нескольких переменных
Найти стационарные точки функций
15.1
15.2
15.3
15.4
15.5
15.6
15.7
15.8
15.9.
15.10
Исследовать на экстремум функции двух переменных
15.11
15.12
15.13
15.14
15.15.
15.16
Найти условный экстремум функции двух переменных
15.17
,
15.18
,
15.19
,
15.20
,
15.21
,
15.22
,
15.23
,
15.24
,
16. Системы линейных неравенств нескольких переменных. Графическое решение
Решить графически системы неравенств и найти все угловые точки
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
16.10
16.11
16.12
16.13
16.14
16.15
16.16
16.17
16.18
16.19
16.20
16.21
16.22
16.23
16.24
17. Простейшие задачи линейного программирования.
Методом градиента исследовать на
экстремум указанную функцию
при указанных ограничениях.
17.1
17.2
17.3
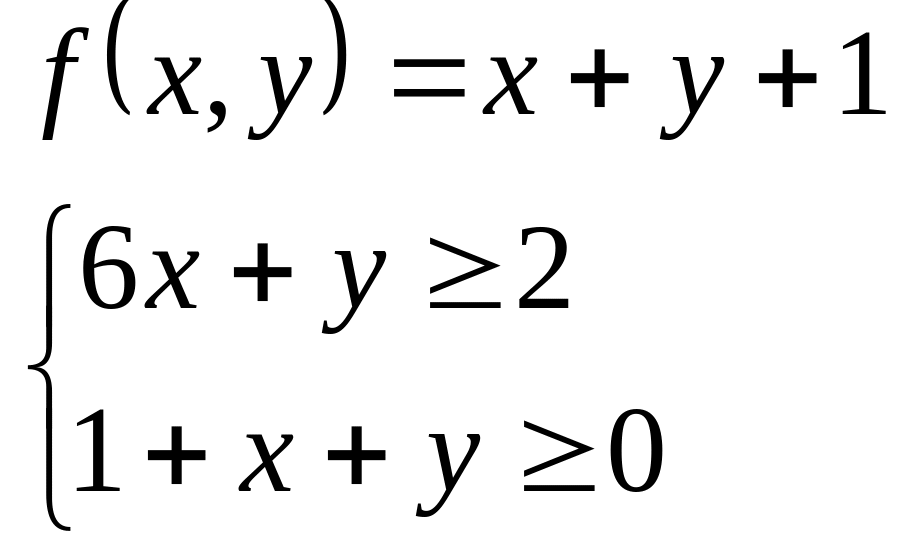17.4
17.5
17.6
17.7
17.8
17.9
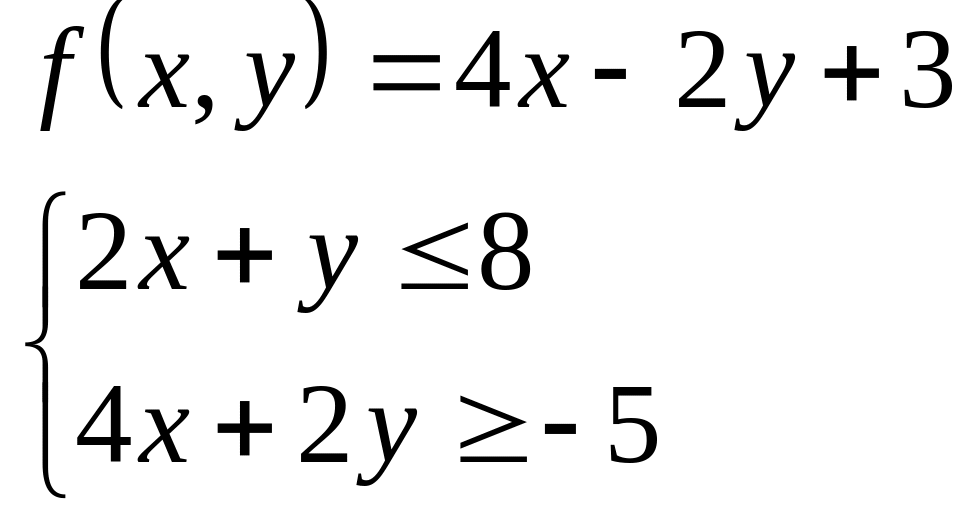17.10
17.11
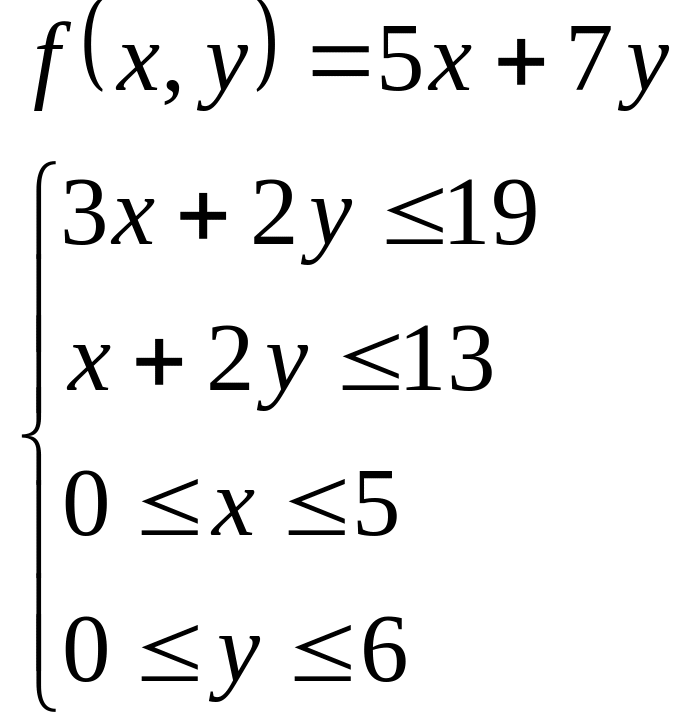17.12
17.13
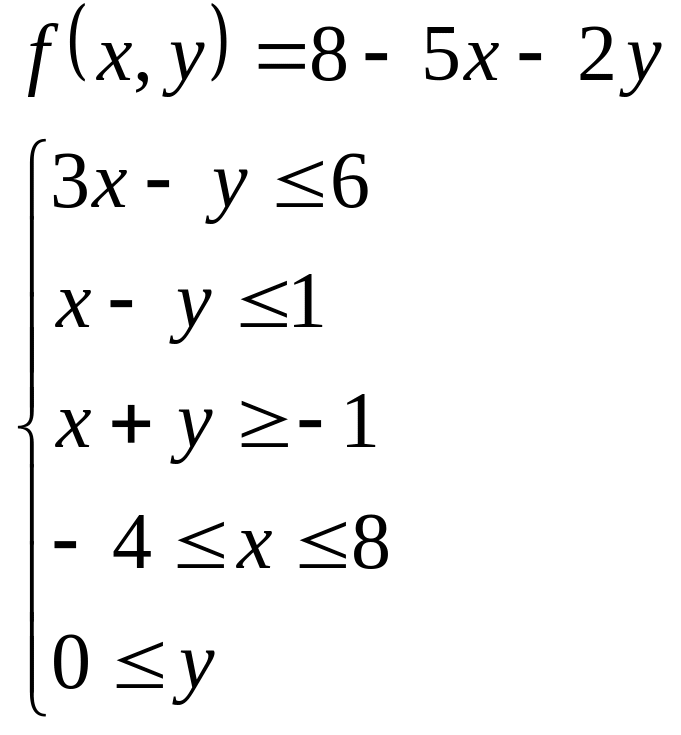17.14
18. Неопределенный интеграл. Основные методы интегрирования
Найти интегралы, используя таблицу интегралов и свойства линейности
18.1
18.2
18.3
18.4
18.5
18.6
18.7
18.8
18.9
18.10
18.11
18.12
18.13
18.14
18.15
18.16
18.17
18.18
18.19
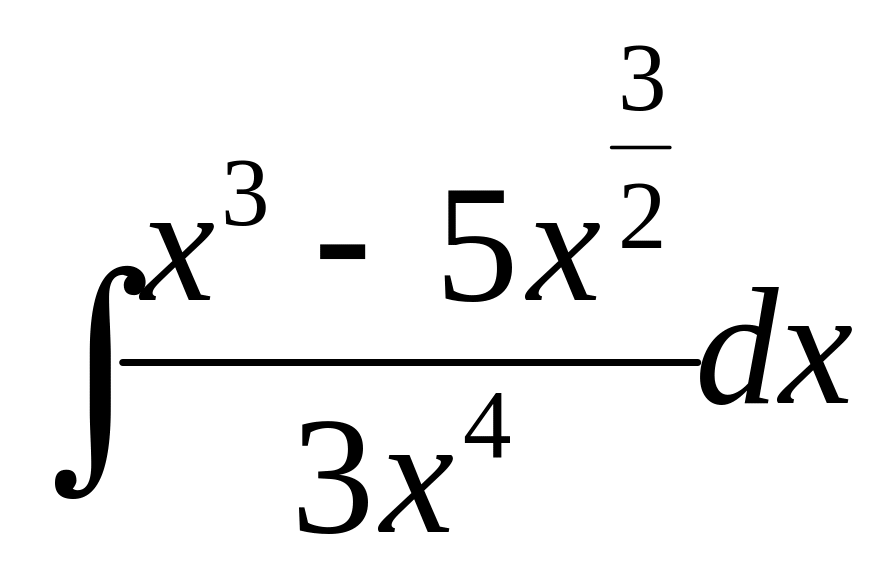18.20
18. 21
18.22
18.23
18.24
18.25
18.26
18.27
18.28
18.29
18.30
18.31
18.32
18.33
18.34
Найти интегралы, используя подведение под знак дифференциала, преобразование подынтегрального выражения
18.35
18.36
18.37
18.38
18.39
18.40
18.41
18.42
18.43
18.44
18.45
18.46
18.47
18.48
18.49
18.50
18.51
18.52
Найти интегралы, используя метод интегрирования по частям
18.53
18.54
18.55
18.56
18.57
18.58
18.59
18.60
Найти интегралы, используя указанную замену переменной
18.61
,
18.62
,
18.63
,
18.64
,
18.65
,
18.66
,
18.67
,
18.68
,
19. Интегралы от рациональных функций
Выделить целую часть рациональной дроби
19.1
19.2
19.3
19.4
19.5
19.6
Разложить правильную рациональную дробь на простейшие дроби
19.7
19.8
19.9
19.10
19.11
19.12
19.13
19.14
Вычислить интегралы от простейших рациональных дробей
19.15
19.16
19.17
19.18
19.19
19.20
19.21
19.22
Вычислить интегралы от рациональных функций
19.23
19.24
19.25
19.26
19.27
19.28
19.29
19.30
19.31
19.32
20. Интегралы от тригонометрических функций
Найти интегралы, используя указанную замену переменной
20.1
,
20.2
,
20.3
,
20.4
,
20.5
,
20.6
,
20.7
,
20.8
,
20.9
,
20.10
,
Найти интегралы, используя формулы понижения степени
20.11
20.12
20.13
20.14
20.15
20.16
21. Интегралы от иррациональных функций
Найти интегралы, используя указанную замену переменной
21.1
,
21.2
,
21.3
,
21.4
,
21.5
,
21.6
,
22. Определенный интеграл. Формула Ньютона-Лейбница
Вычислить интегралы
22.1
22.2
22.3
22.4
22.5
22.6
22.7
22.8
22.9
22.10
Вычислить среднее значение функции на указанном отрезке
22.11
,
22.12
,
22.13
,
22.14
,
22.15
,
22.15
,
23. Замена переменной и интегрирование по частям в определенном интеграле
23.1
23.2
23.3
23.4
23.5
23.6
23.7
23.8
23.9
23.10
24. Применение определенного интеграла для вычисления площадей и длин дуг кривых
Вычислить площадь фигур, ограниченных кривыми, заданными в декартовых координатах, изобразить эти фигуры
24.1
24.2
24.3
24.4
24.5
24.6
24.7
24.8
24.9
24.10
Вычислить площадь фигур, ограниченных кривыми, заданными параметрически, изобразить эти фигуры
24.11
24.12
24.13
24.14
Вычислить длины дуг кривых
24.15
24.16
24.17
24.18