10. Непрерывность функции в точке и на отрезке
Найти значения параметров, при которых функция будет непрерывной
10.1
10.2
10.3
10.4
10.5
10.6
Найти все точки разрыва функции и определить их тип. Построить график в окрестности каждой точки разрыва
10.7
10.8
10.9
10.10
10.11
10.12
10.13
10.14
10.15
10.16
10.17
10.18
10.19
10.20
10.21
10.22
10.23
10.24
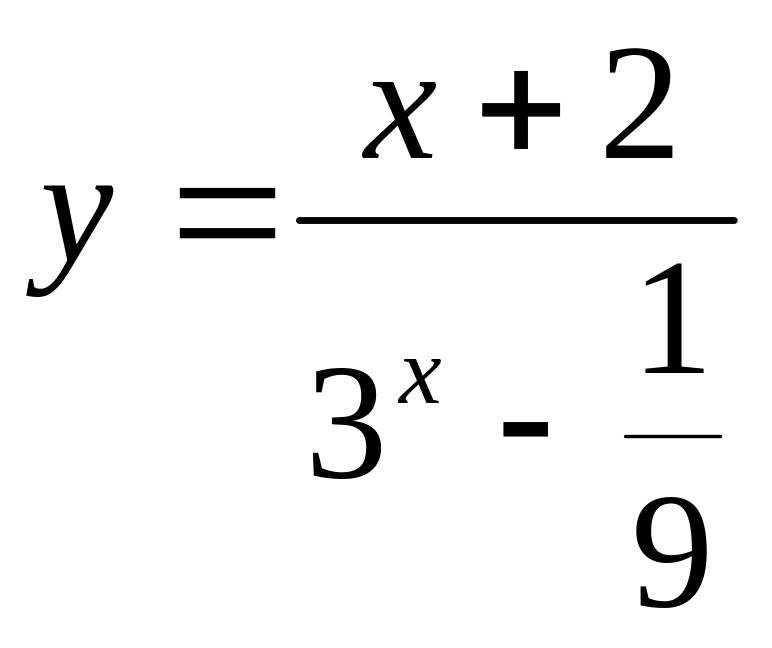
11. Формула Тейлора, ее применение для исследования функций
Написать формулу Тейлора n-го порядка в указанной точке хо
11.1
11.2
11.3
11.4
11.5
11.6
11.7
11.8
11.9
11.10
11.11
11.12
Вычислить приближённо, используя несколько первых членов разложения по формуле Тейлора
11.13
11.14
11.15
11.16
11.17
11.18
11.19
11.20
Исследовать поведение функции в окрестности заданной точки, написав несколько членов разложения функции по формуле Тейлора
11.21
11.22
11.23
11.24
11.25
11.26
12. Функции нескольких переменных.
Найти значения функций нескольких переменных в указанных точках
12.1
12.2
12.3
12.4
12.5
12.6
12.7
12.8
12.9
12.10
Найти и изобразить область определения функции
12.11
12.12
12.13
12.14
12.15
12.16
12.17
12.18
12.19
12.20
12.21
12.22
12.23
12.24
13. Частные производные, градиент.
Найти частные производные 1-го и 2-го порядков и полные дифференциалы для данных функций
13.1
13.2
13.3
13.4
13.5
13.6
13.7
13.8
13.9
13.10
13.11
13.12
13.13
13.14
13.15
13.16
13.17
13.18
13.19
13.20
Найти для данных функций производную
по направлению
в заданной точке
13.21
13.22
13.23
13.24
Изобразить линии уровня и найти вектор градиента для указанных функций
13.25
13.26
13.27
13.28
13.29
13.30
13.31
13.32
13.33
13.34
Записать в явном виде функцию
,
заданную неявно уравнением
13.35
13.36
13.37
13.38
13.39
13.40
13.41
13.42
13.43
13.44
13.45
13.46
Найти производную
от функций, заданных неявно уравнением
13.47
13.48
13.49
13.50
13.51
13.52
13.53
13.54
13.55
13.56
13.57
13.58
13.59
13.60
Найти частные производные
от функций, заданных неявно уравнением
13.61
13.62
13.63
13.64
13.65
13.66
