III. Трёхмерная модель.
Рассмотрим значительно более сложную, а вместе с тем и реалистичную модель в трёхмерном пространстве. Вводим следующие факторы:
- будем учитывать, что в коридоре есть потолок высоты H.
-
материал имеет форму прямоугольного
параллелепипеда с размерами
(длина, ширина, высота).
Как всегда, рисунок проясняет ситуацию:
Для решения задачи рассмотрим те изображения, которые получаются из приведённого рисунка, если посмотреть сверху и с боку. На основе этих рисунков и будем строить своё решение.
Вид сбоку изображен на следующем рисунке.
На
рисунке высота потолка обозначена H,
высота материала равняется m,
длина материала равняется k.
Требуется найти длину проекции данного
материала на пол коридора, то есть
величину L.
Воспользуемся несложными геометрическими
соображениями. Красными чертами на
рисунке изображены углы
.
Из треугольника DCB
имеем следующее определение синуса:
Получившееся уравнение можно решить относительно угла , введя вспомогательный аргумент:
Пусть
,
тогда
Данная
запись согласуется с геометрическим
чертежом, на котором
Зная угол
,
мы легко можем найти интересующую нас
величину L.
Окончательное выражение для Lвыглядит
таким образом:
расширенная запись выглядит следующим образом:
Заметно, что с выражением такого рода работать не легко, поэтому давайте попытаемся упростить его. Пусть
Возьмём
от обеих частей этого равенства
Если
возьмём от обеих частей исходного
равенства
то получим
Таким образом, мы приходим к более удобному выражению для L:
Теперь давайте рассмотрим вид сверху. Длина материала теперь составляет L, а ширина l.
С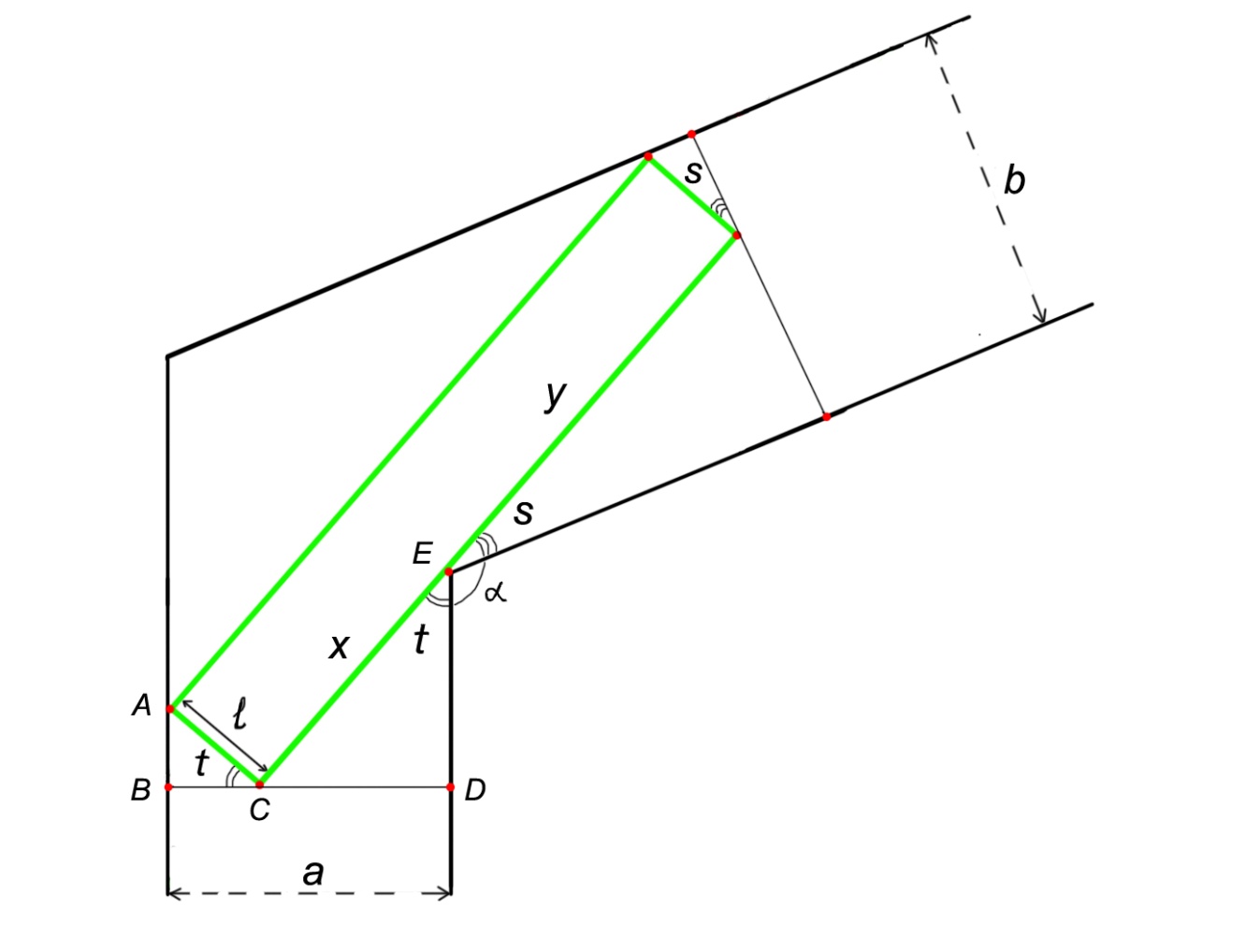
другой стороны, данный рисунок даёт нам
другое выражение для L.
Рассмотрим треугольник CED,
в нём
или
.
По таким же соображениям
.
Суммируя и вспоминая связь между t и s, получаем выражение для L:
,
которое нужно минимизировать. После того, как мы его минимизируем, используя ещё одно выражение для L, мы сможем найти длину материала k, решив соответствующее уравнение. Чтобы долго себя не мучить скучными вычислениями, воспользуемся встроенными в Maple процедурами нахождения производной и численного решения уравнений в заданных интервалах. Следует сделать некоторое уточнение, мы ищем максимальную длину материала при заданных его ширине и высоте. Итак, вот как выглядит алгоритм решение и соответствующая программа:
1) Вводим входные параметры:
a:=2;
b:=2.2;
H:=2;
l:=0.15;
m:=0.2;
alpha:=2*Pi/3;
2) Длина материала как проекция на пол
Lk[proj]:=(k*m*H+(k^2-m^2)*sqrt(k^2+m^2-H^2))/(k^2+m^2);
3) Длина материала, вид сверху
L:=(a-l*cos(t))/sin(t)+(b+l*cos(t+alpha))/sin(t+alpha);
4) Минимизация функции L
T:=fsolve(diff(L,t)=0,t=0..Pi-alpha);
L[min]:=evalf(subs(t=T,L));
5)
Решение уравнения
fsolve(Lk[proj]=L[min],k=0..100);
Последняя строка в программе и есть та самая максимальная длина материала, которую мы ищем. Таким образом, мы снова автоматизировали процесс получения решения.
Давайте ещё посмотрим на графики функций, которые мы рассматривали. В этом нам снова поможет Maple. Итак, вот как выглядит минимизируемая функция:
А вот как выглядит зависимость величины L (длины проекции материала на пол) от длины самого материала.
С облегчением и большим удовлетворением провозглашаем об успешном окончании нашей работы. Спасибо за внимание!